
Tilfældig prøvetagningsmetode, fordele, ulemper, eksempler
Det tilfældig prøveudtagning det er måden at vælge en statistisk repræsentativ prøve fra en given population. En del af princippet om, at hvert element i prøven skal have samme sandsynlighed for at blive valgt.
En lodtrækning er et eksempel på tilfældig stikprøve, hvor hvert medlem af deltagerpopulationen tildeles et nummer. For at vælge de numre, der svarer til lodtrækningspræmierne (prøven), anvendes en tilfældig teknik, f.eks. Udtrækning fra en postkasse af de numre, der blev optaget på identiske kort.
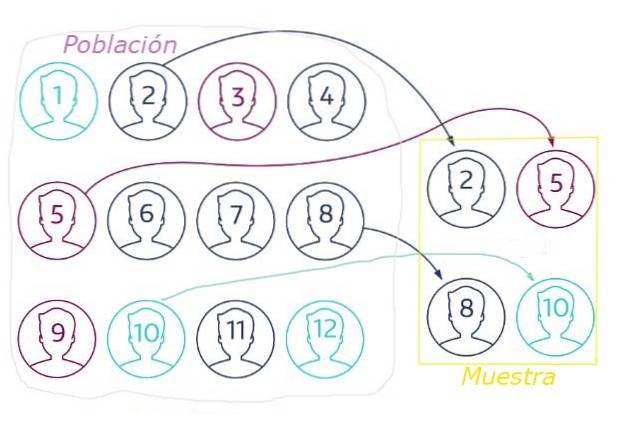
Ved stikprøveudtagning er det vigtigt at vælge stikprøvestørrelsen korrekt, fordi en ikke-repræsentativ stikprøve af befolkningen kan føre til forkerte konklusioner på grund af statistiske udsving..
Artikelindeks
- 1 Prøvestørrelsen
- 1.1 Tilfælde 1: befolkningens størrelse er ukendt
- 1.2 Tilfælde 2: befolkningens størrelse er kendt
- 2 Eksempler
- 2.1 Undersøgelser og spørgeskemaer
- 2.2 Kvalitetskontrol
- 3 fordele
- 4 Ulemper
- 5 Øvelse løst
- 6 Referencer
Størrelsen af prøven
Der er formler til bestemmelse af den rigtige størrelse af en prøve. Den vigtigste faktor at overveje er, om befolkningsstørrelsen er kendt eller ej. Lad os se på formlerne for at bestemme prøvestørrelsen:
Tilfælde 1: befolkningens størrelse er ukendt
Når populationsstørrelsen N er ukendt, er det muligt at vælge en prøve af passende størrelse n for at bestemme, om en bestemt hypotese er sand eller falsk.
Til dette anvendes følgende formel:
n = (Zto p q) / (E.to)
Hvor:
-p er sandsynligheden for, at hypotesen er sand.
-q er sandsynligheden for, at den ikke er det, derfor er q = 1 - p.
-E er den relative fejlmargin, for eksempel har en fejl på 5% en margen E = 0,05.
-Z har at gøre med det niveau af selvtillid, der kræves af undersøgelsen.
I en standardiseret (eller normaliseret) normalfordeling har et konfidensniveau på 90% Z = 1.645, fordi sandsynligheden for, at resultatet er mellem -1.645σ og + 1.645σ er 90%, hvor σ er standardafvigelsen.
Tillidsniveauer og deres tilsvarende Z-værdier
1.- 50% konfidensniveau svarer til Z = 0,675.
2.- 68,3% konfidensniveau svarer til Z = 1.
3.- 90% konfidensniveau svarer til Z = 1.645.
4.- 95% konfidensniveau svarer til Z = 1,96
5.- 95,5% konfidensniveau svarer til Z = 2.
6.- 99,7% konfidensniveau svarer til Z = 3.
Et eksempel, hvor denne formel kan anvendes, ville være i en undersøgelse for at bestemme den gennemsnitlige vægt af småsten på en strand.
Det er klart, at det ikke er muligt at studere og veje alle småsten på stranden, så det tilrådes at udtrække en prøve så tilfældigt som muligt og med det passende antal elementer..

Tilfælde 2: størrelsen af befolkningen er kendt
Når antallet af elementer, der udgør en bestemt population (eller univers), er kendt, hvis du vil vælge en statistisk signifikant prøve af størrelse n ved simpel tilfældig stikprøve, er dette formlen:
n = (Ztop q N) / (N Eto + Ztop q)
Hvor:
-Z er koefficienten forbundet med konfidensniveauet.
-p er sandsynligheden for, at hypotesen lykkes.
-q er sandsynligheden for fiasko i hypotesen, p + q = 1.
-N er størrelsen af den samlede befolkning.
-E er den relative fejl i undersøgelsesresultatet.
Eksempler
Metoden til at udtrække prøverne afhænger meget af, hvilken type undersøgelse der skal foretages. Derfor har tilfældig prøveudtagning et uendeligt antal applikationer:
Undersøgelser og spørgeskemaer
F.eks. Vælges de telefon, der skal høres, i telefonundersøgelser ved hjælp af en tilfældig talgenerator, der gælder for den undersøgte region..
Hvis du vil anvende et spørgeskema til medarbejderne i en stor virksomhed, kan du ty til udvælgelsen af respondenterne gennem deres medarbejdernummer eller identitetskortnummer.
Dette nummer skal også vælges tilfældigt ved hjælp af f.eks. En tilfældig talgenerator.

QA
I tilfælde af at undersøgelsen er på dele fremstillet af en maskine, skal dele vælges tilfældigt, men fra batcher fremstillet på forskellige tidspunkter af dagen eller på forskellige dage eller uger..
Fordel
Enkel tilfældig prøveudtagning:
- Det giver mulighed for at reducere omkostningerne ved en statistisk undersøgelse, da det ikke er nødvendigt at undersøge den samlede befolkning for at opnå statistisk pålidelige resultater med de ønskede konfidensniveauer og det niveau af fejl, der kræves i undersøgelsen.
- Undgå bias: da valget af de elementer, der skal undersøges, er helt tilfældigt, afspejler undersøgelsen trofast befolkningens egenskaber, selvom kun en del af den blev undersøgt.
Ulemper
- Metoden er ikke tilstrækkelig i tilfælde, hvor du vil vide præferencerne i forskellige grupper eller befolkningsstrata.
I dette tilfælde foretrækkes det tidligere at bestemme de grupper eller segmenter, som undersøgelsen skal udføres på. Når strata eller grupper er defineret, så hvis det er hensigtsmæssigt at anvende tilfældig prøveudtagning på hver enkelt af dem..
- Det er meget usandsynligt, at der opnås information om minoritetssektorer, hvor det undertiden er nødvendigt at kende deres egenskaber.
For eksempel, hvis det drejer sig om at lave en kampagne på et dyrt produkt, er det nødvendigt at kende præferencer for de rigeste minoritetssektorer.
Træning løst
Vi ønsker at undersøge befolkningens præference for en bestemt coladrink, men der er ingen tidligere undersøgelse i denne population, hvis størrelse ikke er ukendt..
På den anden side skal prøven være repræsentativ med et minimum konfidensniveau på 90%, og konklusionerne skal have en procentvis fejl på 2%..
-Sådan bestemmes prøvestørrelsen n?
-Hvad ville stikprøvestørrelsen være, hvis fejlmargenen blev lempet til 5%??
Opløsning
Da populationsstørrelsen er ukendt, bruges formlen ovenfor til at bestemme stikprøvestørrelsen:
n = (Ztop q) / (E.to)
Vi antager, at der er lige stor sandsynlighed for præference (p) for vores brand sodavand som for ikke-præference (q), så p = q = 0,5.
På den anden side, da resultatet af undersøgelsen skal have en procentvis fejl mindre end 2%, vil den relative fejl E være 0,02.
Endelig giver en Z-værdi = 1.645 et konfidensniveau på 90%.
Sammenfattende har vi følgende værdier:
Z = 1.645
p = 0,5
q = 0,5
E = 0,02
Med disse data beregnes den mindste stikprøvestørrelse:
n = (1.645to 0,5 0,5) / (0,02to) = 1691,3
Dette betyder, at undersøgelsen med den krævede fejlmargin og med det valgte tillidsniveau skal have en stikprøve af respondenter på mindst 1692 individer, valgt ved simpel tilfældig stikprøve..
Hvis du går fra en fejlmargin på 2% til 5%, er den nye stikprøvestørrelse:
n = (1.645to 0,5 0,5) / (0,05to) = 271
Hvilket er et betydeligt lavere antal individer. Afslutningsvis er stikprøvestørrelsen meget følsom over for den ønskede fejlmargin i undersøgelsen..
Referencer
- Berenson, M. 1985. Statistik for ledelse og økonomi, begreber og applikationer. Redaktionel Interamericana.
- Statistikker. Tilfældig prøveudtagning. Hentet fra: encyclopediaeconomica.com.
- Statistikker. Prøveudtagning. Gendannet fra: Estadistica.mat.uson.mx.
- Undersøgeligt. Tilfældig prøveudtagning. Gendannet fra: explorable.com.
- Moore, D. 2005. Anvendt grundlæggende statistik. 2. plads Udgave.
- Netquest. Tilfældig prøveudtagning. Gendannet fra: netquest.com.
- Wikipedia. Statistisk prøveudtagning. Gendannet fra: en.wikipedia.org



Endnu ingen kommentarer