Egenskaber for komplekse tal, eksempler, operationer

Det komplekse tal er det numeriske sæt, der inkluderer de reelle tal og alle rødderne til polynomierne, inklusive de lige tal for de negative tal. Disse rødder findes ikke i sættet med reelle tal, men i komplekse tal er der løsningen.

Et komplekst tal består af en reel del og en del kaldet "imaginær". Den virkelige del kaldes til, for eksempel og den imaginære del ib, med til Y b reelle tal og "jeg" kan lide imaginær enhed. På denne måde tager det komplekse tal form:

z = a + ib

Eksempler på komplekse tal er 2 - 3i, -πi, 1 + (1/2) i. Men inden vi opererer med dem, lad os se, hvor den imaginære enhed stammer jeg, i betragtning af denne kvadratiske ligning:

x^to - 10x + 34 = 0

Hvor a = 1, b = -10 og c = 34.

Når vi anvender løsningsformlen til at bestemme løsningen, finder vi følgende:

Hvordan bestemmes værdien af ​​√-36? Der er ikke noget reelt tal, der kvadreres, resulterer i en negativ mængde. Derefter konkluderes det, at denne ligning ikke har nogen reelle løsninger.

Vi kan dog skrive dette:

√-36 = √-6^to = √6^to (-1) = 6√-1

Hvis vi definerer en bestemt værdi x sådan at:

x^to = -1

Derefter:

x = ± √-1

Og ovenstående ligning ville have en løsning. Derfor blev den imaginære enhed defineret som:

i = √-1

Også:

√-36 = 6i

Mange matematikere fra oldtiden arbejdede på at løse lignende problemer, især renæssancen Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) og Raffaele Bombelli (1526-1572).

År senere kaldte René Descartes (1596-1650) mængder som √-36 i eksemplet "imaginær". Af denne grund er √-1 kendt som imaginær enhed.

Artikelindeks

• 1 Egenskaber for komplekse tal
• 2 Repræsentation af komplekse tal
  • 2.1 - Binomial form
  • 2.2 - Polær form
• 3 Eksempler på komplekse tal
• 4 Hvad er de til??
• 5 Operationer med komplekse tal
  • 5.1 - Eksempel 1
  • 5.2 - Eksempel 2
• 6 Anvendelse
• 7 Referencer

Egenskaber for komplekse tal

-Sættet med komplekse tal er betegnet C og inkluderer de reelle tal R og de imaginære tal Im. Antalsæt er repræsenteret i et Venn-diagram som vist i følgende figur:

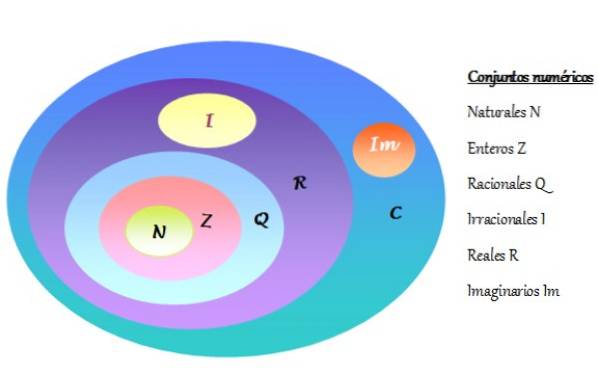
-Hvert komplekst tal består af en reel del og en imaginær del.

-Når den imaginære del af et komplekst tal er 0, er det et rent reelt tal.

-Hvis den reelle del af et komplekst tal er 0, er tallet rent imaginært.

-To komplekse tal er ens, hvis deres respektive virkelige del og imaginære del er de samme.

-Med komplekse tal udføres de kendte operationer af addition, subtraktion, multiplikation, produkt og forbedring, hvilket resulterer i et andet komplekst antal.

Repræsentation af komplekse tal

Komplekse tal kan repræsenteres på forskellige måder. Her er de vigtigste:

- Binomial form

Det er den form, der blev givet i begyndelsen, hvor z er det komplekse tal, til det er den rigtige del, b er den imaginære del e jeg er den imaginære enhed:

z = a + ib

Eller også:

z = x + iy

En måde at tegne det komplekse tal på er gennem det komplekse plan, der er vist i denne figur. Den imaginære akse Im er lodret, mens den virkelige akse er vandret og betegnes som Re.

Det komplekse tal z er repræsenteret på dette plan som et koordinatpunkt (x, y) eller (a, b), som det gøres med punkterne i det virkelige plan.

Afstanden fra oprindelsen til punktet z er modulet for det komplekse tal, betegnet som r, mens φ er den vinkel, der dannes r med den rigtige akse.

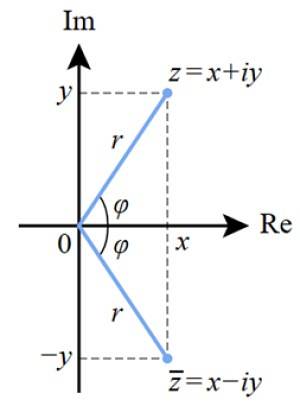
Denne repræsentation er tæt forbundet med vektorerne i det virkelige plan. Værdien af ​​r svarer til modul af det komplekse nummer.

- Polær form

Den polære form består i at udtrykke det komplekse tal ved at give værdierne for r og af φ. Hvis vi ser på figuren, er værdien af r svarer til hypotenusen i en ret trekant. Benene er værd til Y b, O godt x Y Y.

Fra binomial eller binomial form kan vi bevæge os til den polære form ved at:

r = √x^to+Y^to

Vinklen φ Det er den, der danner segmentet r med den vandrette akse eller imaginære akse. Det er kendt som argument af det komplekse nummer. På denne måde:

φ = arctg (y / x)

Argumentet har uendelige værdier under hensyntagen til, at hver gang en drejning drejes, hvilket er værd 2π radianer, indtager r den samme position igen. På denne generelle måde udtrykkes argumentet fra z, betegnet Arg (z), således:

Arg (z) = φ + 2kπ

Hvor k er et heltal og bruges til at angive antallet af drejninger: 2, 3, 4…. Tegnet angiver rotationsretningen, hvis det er med eller mod uret.

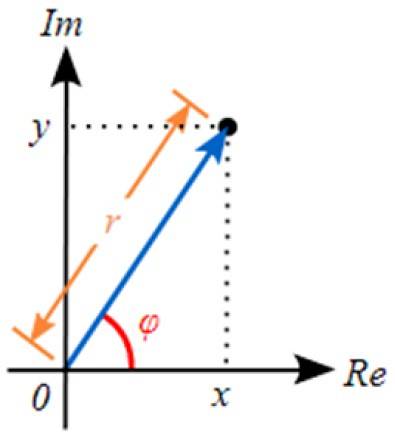
Og hvis vi vil gå fra den polære form til den binomiale form, bruger vi de trigonometriske forhold. Fra den foregående figur kan vi se, at:

x = r cos φ

y = r sin φ

På denne måde z = r (cos φ + i sin φ)

Hvilket forkortes således:

z = r cis φ

Eksempler på komplekse tal

Følgende komplekse tal er angivet i binomial form:

a) 3 + i

b) 4

d) -6i

Og disse i form af et ordnet par:

a) (-5, -3)

b) (0, 9)

c) (7,0)

Endelig er denne gruppe angivet i polær eller trigonometrisk form:

a) √2 cis 45º

b) √3 cis 30º

c) 2 cis 315º

Hvad er de til??

Nytten af ​​komplekse tal går ud over at løse den kvadratiske ligning, der blev vist i starten, da de er vigtige inden for teknik og fysik, især i:

-Undersøgelsen af ​​elektromagnetiske bølger

-Vekselstrøm og spændingsanalyse

-Modellering af alle slags signaler

-Relativitetsteori, hvor tiden antages at være en imaginær størrelse.

Komplekse nummeroperationer

Med komplekse tal kan vi udføre alle de operationer, der udføres med reelle. Nogle er lettere at gøre, hvis tallene kommer i binomial form, såsom addition og subtraktion. I stedet er multiplikation og division enklere, hvis de udføres med den polære form.

Lad os se på nogle eksempler:

- Eksempel 1

Tilføj z₁ = 2 + 5i og z_to = -3 -8i

Opløsning

De virkelige dele tilføjes separat fra de imaginære dele:

z₁ + z_to = (2 + 5i) + (-3 -8i) = -1 -3i

- Eksempel 2

Multiplicer z₁ = 4 cis 45º og z_to = 5 cis 120º

Opløsning

Det kan vises, at produktet af to komplekse tal i polær eller trigonometrisk form er givet ved:

z₁ . z_to = r₁.r_to cis (φ₁ + φ_to)

Ifølge dette:

z₁ . z_to = (4 × 5) cis (45 + 120) = 20 cis 165º

App

En simpel anvendelse af komplekse tal er at finde alle rødderne til en polynomligning som den, der er vist i begyndelsen af ​​artiklen.

I tilfældet med ligningen x^to - 10x + 34 = 0, når vi anvender løsningsformlen får vi:

Derfor er løsningerne:

x₁ = 5 + 3i

x_to = 5 - 3i

Referencer

1. Earl, R. Komplekse numre. Gendannet fra: maths.ox.ac.uk.
2. Figuera, J. 2000. Matematik 1.. Diversificeret. CO-BO udgaver.
3. Hoffmann, J. 2005. Valg af emner i matematik. Monfort-publikationer.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Wikipedia. Komplekse tal. Gendannet fra: en.wikipedia.org