
Negative tal koncept, eksempler, operationer

Det negative tal er de til venstre for nummerlinjen, altid forud for et - tegn. Ved hjælp af negativer er det muligt at repræsentere mængder, der er under eller til venstre for 0.
Disse tal deltager aktivt i hverdagen: for eksempel, hvis nogen har en gæld på $ 5, men kun kan betale $ 3, skylder de $ 2. Gæld betegnes med et negativt tegn for at skelne den fra det betalte beløb.
Positioner under havets overflade, temperaturer under vandets frysepunkt og gulve under gadeniveau kan betegnes med negative tal..
Artikelindeks
- 1 Hvad er negative tal for?
- 2 Handlinger med negative tal
- 2.1 Absolut værdi
- 2.2 Tegn
- 2.3 Summen
- 2.4 Subtraktion
- 2.5 Multiplikation
- 2.6 Opdeling
- 2.7 Bemyndigelse
- 3 Referencer
Hvad er negative tal for?
Eksistensen af negativer udvider de mulige numeriske operationer. Lad os tage eksemplet med subtraktion af to tal. Hvis disse tal hører til det naturlige 1, 2, 3, 4, 5 ... giver subtraktionen kun mening, hvis det sker ved at trække fra et andet tal, der er mindre end det.
Resultatet af operationen 10 - 7 = 3 er rimeligt, da vi i princippet ikke kan tage mere fra en mængde, end den repræsenterer.
Negativer vil dog beskrive denne anden situation godt: vi ønsker at købe noget til en værdi af $ 20, men vi har kun $ 15, og vi låner $ 5 fra en ven. Gæld, som vi har sagt, er markeret med et negativt tegn og dermed 15 - 20 = -5, som læses som "minus 5".
Sættet af negative heltal sammen med det naturlige og 0 udgør det bredeste sæt af heltal Z.
Men de negative kan også være brøkdel eller decimal og tilhører et endnu større sæt: det af de reelle tal R, som inkluderer det rationelle og det irrationelle..
Med dem alle udføres de kendte aritmetiske operationer, idet de passer på at følge nogle enkle regler for tegn, der forklares nedenfor.
Negative antal operationer
Før du udfører operationer med negative tal, skal du oprette nogle enkle regler til håndtering af tegnet (-), der altid skal forudbestilles og rækkefølgen af tallene.
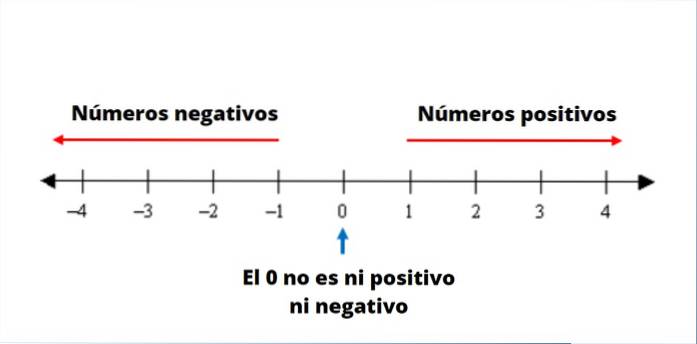
Overvej tallinjen vist i figuren med negativerne til venstre for 0 og de positive til højre.
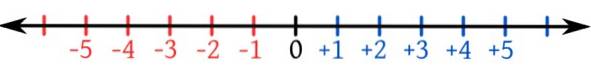
Pile på nummerlinjen i begge retninger angiver, at der er uendelige tal. Bemærk også, at det numeriske sæt heltal er et ordnet sæt, og ethvert negativt tal er mindre end 0 og ethvert positivt tal..
Således er -4 mindre end 1, og -540 er mindre end 84, for eksempel.
Absolut værdi
Afstanden mellem et vilkårligt tal og 0 kaldes absolut værdi. Denne afstand er altid positiv og er betegnet med lodrette søjler, som denne:
│-5│ = 5
│ + √6│ = √6
│-3 / 4│ = 3/4
│-10,2│ = 10,2
Det vil sige, den absolutte værdi af ethvert tal, hvad enten det er positivt eller negativt, er det positive af tallet. Dette koncept hjælper os senere, når vi arbejder med negative tal.
Skilt
En anden meget vigtig detalje er sondringen mellem tegnet på nummeret og operationens tegn..
Når et tal er positivt, udelades tegnets nummer normalt, og det forstås, at det alligevel er positivt, men med negativer, som ikke er mulige, er det derfor nødvendigt at bruge parentes, lad os se:
-Korrekt: 17 - (-6) eller også +17 - (-6)
-Forkert: 17 - -6
-Forkert: -5 + +7
-Korrekt: - 5 + (+7) eller også -5 + 7
Når begreberne absolut værdi, orden og betydning af det negative tegn er klare, kan vi gå videre til de grundlæggende operationer.
Sum
Vi skelner mellem følgende tilfælde, begyndende med summen af to positive, hvis procedure allerede er meget velkendt:
-Tilføj to positive tal: (+ a) + (+ b) = a + b
Hvilket betyder, at vi tilføjer som normalt, lad os se:
(+8) + (+5) = 8 + 5 = 13
-Tilføj to negative tal: (-a) + (-b) = - (a + b)
I dette tilfælde tilføjer vi de absolutte værdier for tallene, og resultatet forudses med et negativt tegn som dette:
(-7) + (-11) = - (7+ 11) = - 18
-Tilføj et negativt og et positivt: (+ a) + (-b)
Til denne operation trækkes de absolutte værdier, og resultatet bærer tegnet på tallet med den højeste absolutte værdi. Lad os gøre nogle sager:
a) (-16) + (+3)
De respektive absolutte værdier er 16 og 3, tallet med den højeste absolutte værdi er 16, hvis tegn er negativt, derefter:
(-16) + (+3) = - (16 - 3) = -13
b) (+8) + (-3) = + (8-3) = +5 = 5
Summen af negativer er også kommutativ, hvilket betyder, at rækkefølgen af tilføjelser ikke er vigtig for resultatet..
De tidligere regler gælder, hvis du vil tilføje mere end to tal, hvilket kan gøres med den associerende egenskab: a + b + c = (a + b) + c = a + (b + c).
Før vi ser på et eksempel i dette tilfælde, lad os først se på subtraktion af to hele tal.
Subtraktion
Subtraktion er defineret som summen af det modsatte. Det modsatte af et tal a er -a, som dette:
-4 er det modsatte af + 4
½ er det modsatte af -½
Hvis vi bliver bedt om at udføre subtraktion af to tal uanset tegnet, tilføjer vi simpelthen det modsatte af det andet til det første:
a) (-53) - (+8) = (-53) + (-8) = - (53 + 8) = -61
b) (+7) - (-12) = (+7) + (+12) = 7 + 12 = 19
c) (+2) - (+ π) = (+2) + (-π) = 2 - π
Eksempel
Udfør følgende handling (+4) + (-7) + (+19)
Vi omskriver det sådan ved hjælp af parenteser for at indikere den operation, der skal udføres først:
(+4) + (-7) + (+19) = [(+4) + (-7)] + (+19) = [- (4-7)] + 19 = [- (-3)] + 19 = 19 - (-3) = 19 + (+3) = 22
Multiplikation
Reglen om tegn til multiplikation er opsummeret i følgende figur:
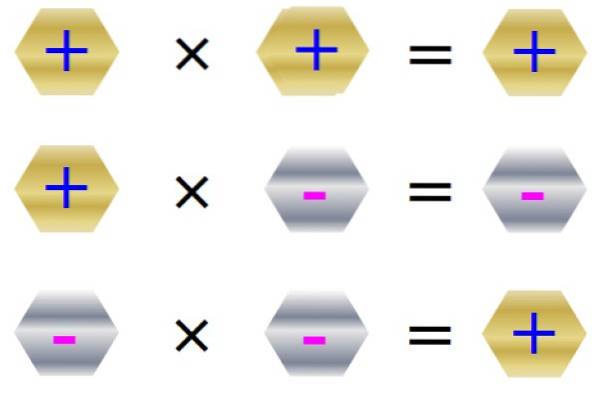
Multiplikationens egenskaber
-Kommutativitet: rækkefølgen af faktorer ændrer ikke produktet, derfor er ≠ = b.a hvor a og b er negative, heltal eller brøktal.
-Associativitet: Lad a, b og c være heltal, det er rigtigt, at (a.b). c = a. (b.c)
-Distributivitet med hensyn til summen: lad a, b og c være heltal, det er gyldigt, at a. (b + c) = a.b + a.c
Eksempel
(-3/2) x [(-5) + (+4) - (+2)] = (-3/2) x (-5) + (-3/2) x (+4) + (- 3/2) x (-2) = (15 - 12 + 6) / 2 = 9/2
Du kunne også have løst operationen i parentes først og gange resultatet med (-3/2), som dette:
(-3/2) x [-5 + 4 - 2] = (-3/2) x (-3) = 9/2
Division
Reglen om tegn til opdeling er vist i følgende figur:
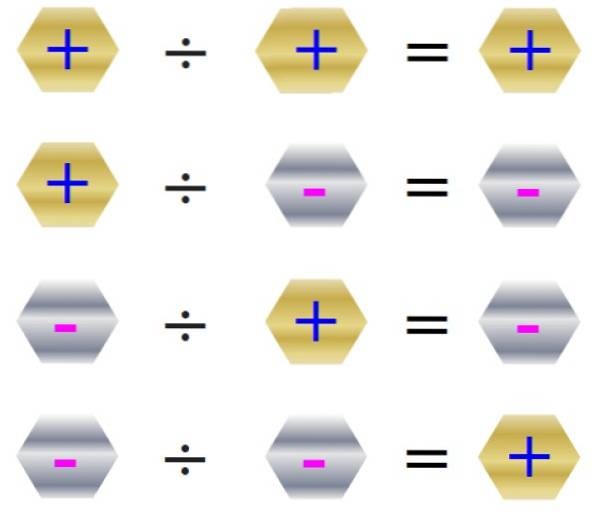
Opdeling er ikke kommutativ og normalt a ÷ b ≠ b ÷ a, deling med 0 er ikke tilladt. Lad os se et eksempel:
(-54) ÷ (+3) = -18
For at opnå dette resultat skal du blot oprette kvotienten og tegnet vælges i henhold til tabellen vist i figuren, hvilket svarer til den tredje mulighed fra top til bund.
Bemyndigelse
Empowerment er driften af formen an, hvor a er basen og n er eksponenten. Basen og eksponenten kan have ethvert tegn.
-Hvis basen er negativ eller positiv, og eksponenten er et lige heltal, er resultatet af operationen altid positivt.
-Når basen er positiv, og eksponenten er et ulige heltal, er resultatet positivt.
-Og hvis basen er negativ, og eksponenten er et ulige heltal, er resultatet negativt.
Brøkeksponenter udtrykkes alternativt som en rod, for eksempel er en kvadratrode svarende til den fraktionerede eksponent ½, en terningrod svarer til eksponenten 1/3 og så videre.
Lad os se på nogle eksempler:
a) (-3)3 = (-3) x (-3) x (-3) = -27
b) 16 -1/2 = 1 / √16 = ¼
c) (+8) 1/3 = terningens rod på 8 = 2
Referencer
- Baldor, A. 1986. Aritmetik. Codex-udgaver og distributioner.
- Figuera, J. 2000. Matematik 7.. Karakter. CO-BO udgaver.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematik er sjovt. Sådan tilføjes og trækkes positive og negative tal. Gendannet fra: mathisfun.com
- Wikipedia. Negative tal. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer