
Perfekte tal, hvordan man identificerer dem og eksempler

EN perfekt tal er et naturligt tal sådan, at summen af dens skillevægge er det samme som antallet. Selve antallet kan selvfølgelig ikke medtages mellem delerne.
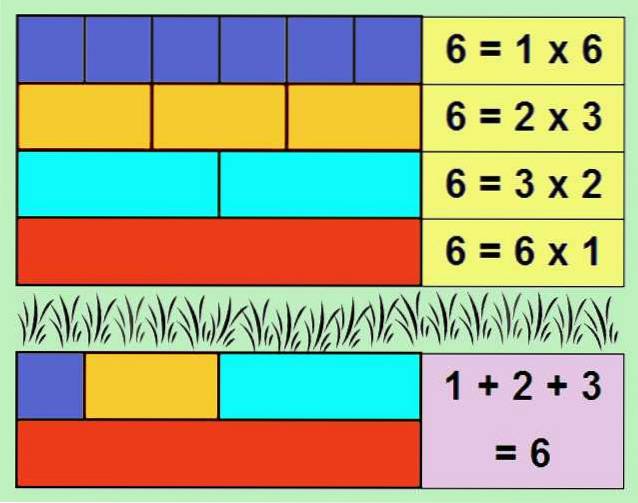
Et af de enkleste eksempler på et perfekt tal er 6, da dets skillevægge er: 1, 2 og 3. Hvis vi tilføjer skillevægge, får vi: 1 + 2 + 3 = 6.
Summen af delerne af et heltal kaldes ikke selve tallet alikvot. Derfor er et perfekt tal lig med dets alikvot.
Men hvis selve tallet er inkluderet i summen af delere af et tal, vil et perfekt tal være et, at summen af alle dets delere divideret med 2 er lig med selve tallet..
Artikelindeks
- 1 Historie
- 2 Egenskaber for perfekte tal
- 2.1 Euclids formel og kriterium
- 2.2 Det største kendte perfekte tal
- 2.3 Et perfekt nummer er venner med sig selv
- 3 Eksempler på perfekte tal
- 4 Øvelser
- 4.1 - Øvelse 1
- 4.2 - Øvelse 2
- 4.3 - Øvelse 3
- 4.4 - Øvelse 4
- 5 Referencer
Historie
Antikens matematikere, især grækerne, tillagde stor betydning for perfekte tal og tilskrev dem guddommelige kvaliteter..
For eksempel bekræftede Philo af Alexandria mod det første århundrede, at 6 og 28 er perfekte tal, der falder sammen med de seks dage, hvor verden blev skabt, og de otteogtyve dage, det tager for månen at gå rundt på jorden..
Perfekte tal er også til stede i naturen, for eksempel vises på det nordlige pol af Saturn det perfekte nummer 6 også, en sekskantformet vortex fundet af Cassini-sonden, og som forskere har fascineret..
Bienes bikager har celler i sekskantet form, dvs. med 6 sider. Det er blevet vist, at polygonen med det perfekte nummer 6 er den, der tillader maksimering af antallet af celler i bikuben med et minimum af voks til dens udarbejdelse..

Egenskaber for perfekte tal
Summen af alle delere af et naturligt tal n er betegnet med σ (n). I et perfekt tal er det tilfreds, at: σ (n) = 2n.
Euclids formel og kriterier
Euclid opdagede en formel og et kriterium, der gør det muligt at finde de perfekte tal. Denne formel er:
to(n-1) (ton -1)
Imidlertid vil antallet, der genereres af formlen, kun være perfekt, når faktoren (2n -1) være en fætter.
Lad os se, hvordan de første perfekte tal genereres:
Hvis n = 2, er vi tilbage med 21 (toto - 1) = 2 x 3 = 6, som vi allerede har set, er perfekt.
Når n = 3 har vi 2to (to3 - 1) = 4 x 7 = 28, hvilket også er perfekt som bekræftet detaljeret i eksempel 1.
Lad os se, hvad der sker med n = 4. Når vi udskifter i Euclids formel, har vi:
to3 (to4 - 1) = 8 x 15 = 120
Det kan verificeres, at dette tal ikke er perfekt, som vist detaljeret i eksempel 3. Dette modsiger ikke Euclids kriterium, da 15 ikke er prime, et nødvendigt krav for at resultatet skal være et perfekt tal.
Lad os nu se, hvad der sker, når n = 5. Anvendelse af den formel, vi har:
to4 (to5 - 1) = 16 x 31 = 496
Da 31 er et primtal, skal tallet 496 være perfekt i henhold til Euclids kriterier. I eksempel 4 er det vist detaljeret, at det faktisk er.
Primtal, der har form 2s - 1 kaldes Mersenne fætre, efter munken Marin Mersenne, der studerede primtal og perfekte tal tilbage i det 17. århundrede..
Senere i det 18. århundrede viste Leonhard Euler, at alle perfekte tal genereret af Euclids formel er lige.
Til dato er der ikke fundet nogen perfekt, der er underlig.
Det største kendte perfekte nummer
Til den nuværende dato kendes 51 perfekte tal, som alle genereres efter formlen og Euclids kriterium. Dette nummer blev opnået, når den større Mersenne fætter blev fundet, hvilket er: (282589933 - 1).
Det perfekte nummer # 51 er (282589933) x (282589933 - 1) og har 49724095 cifre.
Et perfekt nummer er venner med sig selv
I talteori siges det, at to tal er venner, når summen af delere af en, ikke inklusive selve nummeret, er lig med det andet tal og omvendt.
Læseren kan verificere, at summen af delerne på 220, ikke inklusive 220, er 284. På den anden side er summen af delerne på 284, ikke inklusive 284, lig med 220. Derfor er antallet af tal 220 og 284 venner.
Fra dette synspunkt er et perfekt nummer venner med sig selv..
Eksempler på perfekte tal
De første otte perfekte tal er angivet nedenfor:
6
28
496
8128
33550336
8589869056
137438691328
2305843008139952128
Uddannelse
I de følgende øvelser vil det være nødvendigt at beregne delerne af et tal for derefter at tilføje dem og kontrollere, om tallet er et perfekt tal eller ej..
Derfor, inden vi nærmer os øvelserne, gennemgår vi konceptet og viser, hvordan de beregnes..
Til at begynde med skal du huske, at tal kan være primtal (når de kun kan deles nøjagtigt med sig selv og 1) eller sammensatte (når de kan nedbrydes som et produkt med primtal).
For et sammensat tal N har vi:
N = an . bm. cs ... rk
Hvor a, b, c ... r er primtal og n, m, p ... k er eksponenter, der hører til de naturlige tal, som kan være fra 1 og fremefter.
Med hensyn til disse eksponenter er der en formel til at vide, hvor mange delere tallet N har, skønt det ikke fortæller os, hvad det er. Lad C være denne mængde, så:
C = (n +1) (m + 1) (p +1) ... (k + 1)
Nedbrydning af tallet N som et produkt af primtal og at vide, hvor mange delere det har, både primær og ikke-primær, hjælper os med at bestemme, hvad disse delere er..
Når du har dem alle, undtagen den sidste, der ikke kræves i summen, kan du kontrollere, om det er et perfekt tal eller ikke.
- Øvelse 1
Kontroller, at tallet 28 er perfekt.
Opløsning
Den første ting vil være at nedbryde antallet i dets primære faktorer.
28 | 2
14 | 2
07 | 7
01 | 1
Deleinddelerne er: 1, 2, 4, 7, 14 og 28. Hvis vi udelukker 28, giver summen af delerne:
1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28
Derfor er 28 et perfekt tal.
Desuden er summen af alle dens skillevægge 28 + 28, så reglen σ (28) = 2 x 28 er opfyldt.
- Øvelse 2
Beslutter, om nummeret 38 er perfekt eller ej.
Opløsning
Nummeret nedbrydes i dets primære faktorer:
39 | 3
13 | 13
01 | 1
Delerne på 39 uden at inkludere selve tallet er: 1, 3 og 13. Summen 1 + 3 + 13 = 4 + 13 = 17 er ikke lig med 39, derfor er 39 et ufuldkommen eller ikke-perfekt tal.
- Øvelse 3
Find ud af om nummer 120 er perfekt eller ufuldkommen.
Opløsning
Vi fortsætter med at nedbryde antallet i dets primære faktorer:
120 | 2
060 | 2
30 | 2
15 | 3
5 | 5
1 | 1
Fra de vigtigste faktorer fortsætter vi med at finde skillevægge:
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 og 120
Hvis 120 var perfekte, skulle tilføjelse af alle dens skille få 2 x 120 = 240.
1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360
Dette resultat adskiller sig klart fra 240, så det konkluderes, at tallet 120 ikke er et perfekt tal..
- Øvelse 4
Kontroller, at tallet 496, opnået ved Euclids kriterium, er et perfekt tal.
Opløsning
Talet 496 nedbrydes i dets primære faktorer:
496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1
Så dens skillevægge er:
1, 2, 4, 8, 16, 31, 62, 124, 248, 496
Nu er alle tilføjet, undtagen 496:
1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496
Bekræfter, at det virkelig er et perfekt nummer.
Referencer
- Baldor, A. 1986. Aritmetik. Codex-udgaver og distributioner.
- Alt om primtal. Venlige tal. Gendannet fra: numeroprimos.org.
- Wolfram MathWorld. Eulers regel. Gendannet fra: mathworld.wolfram.com.
- Wolfram MathWorld. Perfekt nummer. Gendannet fra: mathworld.wolfram.com.
- Wikipedia. Perfekte tal. Gendannet fra: en.wikipedia.org.
- Wikipedia. Venlige tal. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer