
Stående bølger formler, egenskaber, typer, eksempler
Det stående bølger De er bølger, der formerer sig i et begrænset medium, går og kommer i en del af rummet, i modsætning til vandrende bølger, som når de formerer sig bevæger sig væk fra den kilde, der stammer fra dem og ikke vender tilbage til det.
De er grundlaget for lydene, der produceres i musikinstrumenter, da de let opstår i de faste strenge, enten i den ene ende eller begge dele. De er også skabt i tætte membraner såsom tromler eller inde i rør og strukturer som broer og bygninger..
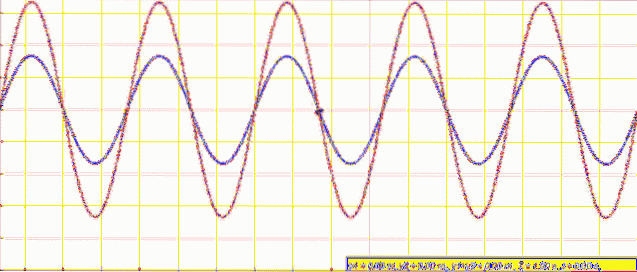
Når du har en fast streng i begge ender, som f.eks. En guitar, oprettes der bølger med identisk amplitude og frekvens, som bevæger sig i modsatte retninger og kombineres for at producere et fænomen kaldet interferens.
Hvis bølgerne er i fase, er toppe og dale justeret og resulterer i en bølge med dobbelt amplitude. I så fald taler vi om konstruktiv indblanding.
Men hvis de forstyrrende bølger er ude af fase, møder toppe på en andres dale, og den resulterende amplitude er nul. Det handler så om destruktiv indblanding.
Artikelindeks
- 1 Formler og ligninger
- 1.1 Matematisk udtryk for den stående bølge
- 2 Placering af knuder og mave
- 2.1 Normale tilstande på en streng
- 2.2 Hastighed og frekvens
- 3 Karakteristika for stående bølger
- 4 typer
- 4.1 Stående bølger i en dimension
- 4.2 Stående bølger i to og tre dimensioner
- 5 eksempler på stående bølger
- 5.1 Faste reb
- 5.2 Musikinstrumenter
- 5.3 Bygninger og broer
- 5.4 Seiches
- 5.5 Fiskeskåle
- 6 Øvelse løst
- 6.1 Løsning a
- 6.2 Løsning b
- 6.3 Løsning c
- 7 Referencer
Formler og ligninger
Hovedelementerne i bølgen, der repræsenterer den i rum og tid, er dens amplitude A, dens bølgelængde λ og dens vinkelfrekvens ω.
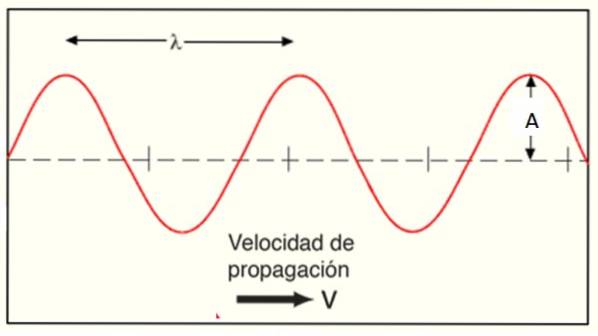
I den matematiske repræsentation foretrækkes det at bruge k, end bølgenummer eller antal gange bølgen opstår pr. længdeenhed. Derfor defineres det gennem bølgelængden λ, som er afstanden mellem to dale eller to kamme:
k = 2π / λ
Mens vinkelfrekvens vedrører perioden eller varigheden af en komplet svingning, såsom:
ω = 2π / T
Og også frekvensen f er givet af:
f = ω / 2π
Derfor:
f = 1 / T
Også bølgerne bevæger sig med hastighed v ifølge:
v = λ.f
Matematisk udtryk for den stående bølge
Matematisk kan vi udtrykke en bølge ved hjælp af sinusfunktionen eller cosinusfunktionen. Antag, at vi har bølger med lige amplitude A, bølgelængde λ og frekvens ω, der forplantes langs en streng og i modsatte retninger:
Y1 = En synd (kx - ωt)
Yto = En synd (kx + ωt)
Når vi tilføjer dem, finder vi den resulterende bølge ogR:
YR = og1 + Yto = A sin (kx - ωt) + A sin (kx + ωt)
Der er en trigonometrisk identitet for at finde summen:
sin α + sin β = 2 sin (α + β) / 2. cos (α - β) / 2
Ved denne identitet, den resulterende bølge yR forbliver:
YR = [2A sin kx]. cos ωt
Placering af knuder og mave
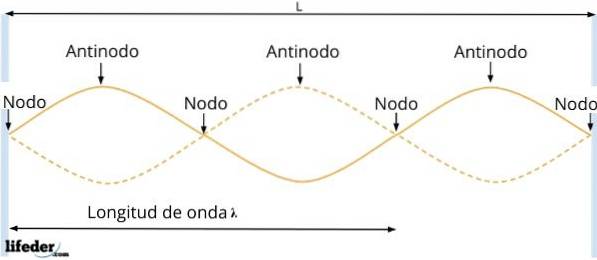
Den resulterende bølge har amplitude A.R = 2Asen kx, hvilket afhænger af partikelens position. På de punkter, for hvilke sin kx = 0, forsvinder bølgens amplitude, dvs. der er ingen vibrationer.
Disse punkter er:
kx = π, 2π, 3π ...
Da k = 2 π / λ:
(2 π / λ) x = π, 2π, 3π ...
x = λ / 2, λ, 3λ / 2 ...
Destruktiv interferens forekommer på sådanne punkter og kaldes noder. De er adskilt med en afstand lig med λ / 2, som trukket fra det foregående resultat.
Og mellem to på hinanden følgende noder er antinoder eller maver, hvor amplituden af bølgen er maksimal, da konstruktiv interferens opstår der. De opstår, når:
sin kx = ± 1
kx = ± π / 2, 3π / 2, 5π / 2 ...
Igen k = 2 π / λ og derefter:
x = λ / 4, 3λ / 4, 5λ / 4,…
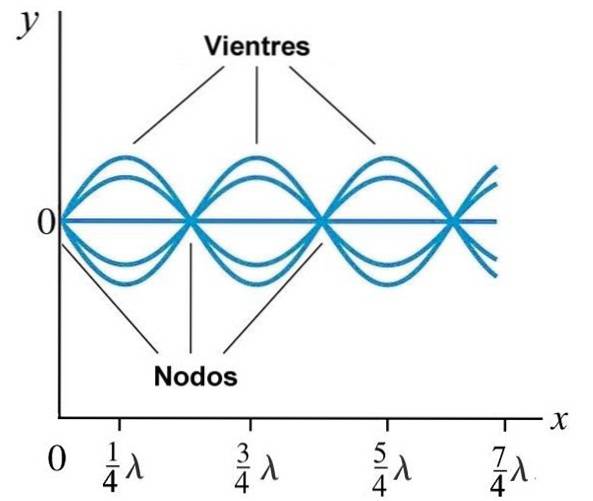
Normale tilstande på en streng
Grænsebetingelserne i strengen bestemmer, hvordan bølgelængderne og frekvenserne er. Hvis en streng af længden L er fast i begge ender, kan den ikke vibrere med nogen frekvens, fordi de punkter, hvor strengen er fast, allerede er noder.
Desuden er adskillelsen mellem tilstødende noder λ / 2, og mellem node og mave er λ / 4, på denne måde produceres der kun for bestemte bølgelængder stationære bølger: dem, hvor et heltal n af λ / 2 passer inden for:
(λ / 2) = L, med n = 1, 2, 3, 4 ... .
Derfor:
λ = 2L / n
Harmoniske
De forskellige værdier, som λ tager, kaldes harmoniske. Således har vi:
-Første harmoniske: λ = 2L
-Anden harmonisk: λ = L
-Tredje harmonisk: λ = 2 L / 3
-Fjerde harmoniske: λ = L / 2
Og så videre.
Hastighed og frekvens
Selvom den stående bølge ikke ser ud til at bevæge sig, er ligningen stadig gyldig:
v = λ. F
Derfor:
v = (2L / n). F
f = nv / 2L
Nu kan det vises, at hastigheden, hvormed en bølge bevæger sig i en streng, afhænger af spændingen T i den og dens lineære massefylde μ (masse pr. Længdeenhed) som:

Derfor:

Karakteristik af stående bølger
-Når bølgerne er stationære, forplantes den resulterende bølge ikke det samme som dens komponenter, som går fra den ene side til den anden. Der er punkter, hvor y = 0, fordi der ikke er nogen vibration: noderne, med andre ord amplituden A.R det bliver nul.
-Det matematiske udtryk for en stående bølge består af produktet af en rumlig del (som afhænger af x-koordinaten eller den geografiske koordinater) og en tidsmæssig del.
-Mellem knudepunkterne svinger den resulterende sorte bølge ét sted, mens bølgerne, der går fra den ene side til den anden, er ude af fase der..
-Energi transporteres ikke lige ved knudepunkterne, da dette er proportionalt med kvadratet på amplituden, men det er fanget mellem knudepunkterne.
-Afstanden mellem tilstødende noder er halv bølgelængde.
-De punkter, hvor akkorden er fast, betragtes også som noder..
Typer
Stående bølger i en dimension
Bølgerne i en fast streng er eksempler på stående bølger i en dimension, hvis matematiske beskrivelse vi tilbød i de foregående afsnit..
Stående bølger i to og tre dimensioner
Stående bølger kan også præsenteres i to og tre dimensioner, hvor deres matematiske beskrivelse er lidt mere kompleks.
Eksempler på stående bølger
Faste reb
-Et reb fastgjort i den ene ende, der er oscilleret i hånden eller med et stempel på den anden, genererer stående bølger langs dets længde.
Musikinstrumenter

-At spille strengeinstrumenter som guitar, harpe, violin og klaver skaber også stående bølger, da de har strenge justeret til forskellige spændinger og fastgjort i begge ender.
Stående bølger oprettes også i rør med luft, såsom orgelrør..
Bygninger og broer
Stående bølger opstår i strukturer som broer og bygninger. Et bemærkelsesværdigt tilfælde var Tacoma Narrows-hængebroen nær Seattle, USA. Kort efter at være blevet indviet i 1940, kollapsede denne bro på grund af de stående bølger, der blev skabt inde af vinden..
Vindens frekvens blev parret med broens naturlige frekvens, hvilket skabte stående bølger i den, som steg i amplitude, indtil broen kollapsede. Fænomenet er kendt som resonans.
Seiches
I havne er der et meget nysgerrig fænomen kaldet seiche, hvor bølgerne i havet producerer store svingninger. Dette skyldes det faktum, at vandet i havnen er ret lukket, selvom havvandene trænger ind imellem ind gennem havnen..
Havnevand bevæger sig med deres egen frekvens, ligesom dem i havet. Hvis begge farvande svarer til deres frekvenser, produceres en stor stående bølge ved resonans, som det skete med Tacoma-broen..
Det seiches De kan også forekomme i søer, reservoirer, svømmebassiner og andre overfladebegrænsede vandområder..
Fisketanke
Stående bølger kan oprettes i en akvarium, der bæres af en person, hvis den frekvens, som personen går med, er lig med frekvensen af vandets svajning.
Træning løst
En guitarstreng har L = 0,9 m og en lineær massefylde μ = 0,005 kg / m. Den udsættes for 72 N spænding, og dens vibrationsmåde er den, der er vist i figuren, med amplitude 2A = 0,5 cm.
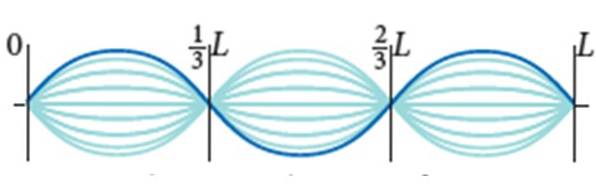
Finde:
a) Formationshastighed
b) Bølgefrekvens
c) Den tilsvarende stående bølgeligning.
Løsning til
Igennem:

Er opnået;
v = [72 N / (0,005 kg / m)]1/2 = 120 m / s.
Løsning b
Afstanden mellem to tilstødende noder er λ / 2, derfor:
(2/3) L - (1/3) L = λ / 2
(1/3) L = λ / 2
λ = 2L / 3 = 2 x 0,90 m / 3 = 0,60 m.
Da v = λ.f
f = (120 m / s) / 0,60 m = 200 s-1= 200 Hz.
Løsning c
Ligningen er:
YR = [2A sin kx]. cos ωt
Vi er nødt til at erstatte værdierne:
k = 2π / λ = k = 2π / 0,60 m = 10 π / 3
f = ω / 2π
ω = 2π x 200 Hz = 400 π Hz.
Amplituden 2A er allerede givet af udsagnet:
2A = 0,5 cm = 5 x 10 -3 m.
Derfor:
YR = 5 x 10 -3 m. sin [(10π / 3) x]. cos (400πt) =
= 0,5 cm. sin [(10π / 3) x]. cos (400πt)
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 7. Bølger og kvantefysik. Redigeret af Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.
- Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 1. Editorial Reverté.
- Wikipedia. Seiche. Gendannet fra: es.wikipedia.org.


Endnu ingen kommentarer