
Tre-dimensionelle bølger koncept, typer og eksempler
De er tredimensionelle bølger dem, der formerer sig i rummet, for eksempel lydbølgen produceret af en højttaler. Denne bølge spreder sig i alle retninger, men ikke med den samme intensitet i dem alle..
Hvis der opstår en forstyrrelse et sted i rummet, formeres den i de tre rumlige retninger, idet bølgefronterne er lukkede overflader, sfæriske, elliptiske eller af en anden type..

På den anden side, hvis det sted, hvor bølgerne stammer, det vil sige kilden, har en flad fordeling, vil forstyrrelsen hovedsageligt bevæge sig i retningen vinkelret på nævnte plan og danne flade bølgefronter..
Artikelindeks
- 1 Typer af tredimensionelle bølger
- 1.1 Flybølger
- 1.2 Cylindriske bølger
- 1.3 Sfæriske bølger
- 2 Intensitet og energi af en sfærisk bølge
- 3 Eksempler på tredimensionelle bølger
- 3.1 Antenner, der udsender elektromagnetiske bølger
- 3.2 Seismiske bølger
- 3.3 Lyden
- 4 Referencer
Typer af tredimensionelle bølger
I tredimensionelle bølger er bølgefronter et sæt overflader nedsænket i tredimensionelt rum.
Nu er bølgefronten stedet for de punkter i rummet, der nås ved den oprindelige forstyrrelse, på samme øjeblik..
Det betragtes normalt som tre typer bølger, der bevæger sig i et tredimensionelt rum i henhold til symmetrien på bølgefronten: plane bølger, cylindriske bølger og sfæriske bølger. Imidlertid hører virkelige bølger ikke altid til disse typer, fordi de ikke har så høj grad af symmetri.
Flade bølger
En plan bølge, der bevæger sig i positiv x-retning med hastighed v, er funktionelt repræsenteret som:
g (x, t) = f (x - v⋅t)
Denne bølge er ikke begrænset til aksen x, det strækker sig også i retningerne Y Y z. Men den funktionelle form fortæller os, at alle punkter, der har den samme x-koordinat, uanset koordinaterne (z, y), har den samme g-værdi.
I dette tilfælde er bølgefronterne planer parallelt med z-y-planen, der bevæger sig hurtigt v, hvilket betyder, at planbølgen optager alle tredimensionelle rum.
Udtrykket, der repræsenterer en plan bølge, der formerer sig i enhver retning eller hurtigt v, hvor eller repræsenterer en enhedsvektor af direktorkosinus cos (α), cos (β) Y cos (γ), det er:
g = f (û • r - v⋅t) = f (x cos (α) + y cos (β) + z cos (γ) - v⋅t)
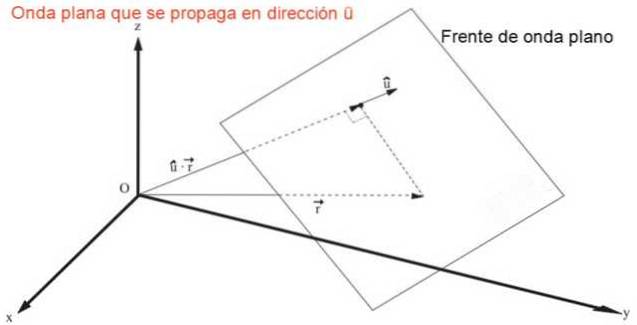
Det er let at vise ved direkte erstatning, at det foregående udtryk er en opløsning af den tredimensionelle bølgeligning, en ligning i partielle derivater af den anden lineære rækkefølge:
∂xxg + ∂yyg + ∂zzg = (1 / volto) ∂ttg
Ovenstående ligning kan skrives mere kompakt ved hjælp af Laplacian-operatoren ∇to:
∇tog = (1 / volto) ∂ttg
Cylindriske bølger
Når den oprindelige forstyrrelse fordeles over en lige linje, udbreder bølgen sig i radial retning vinkelret på den linje og fylder det tredimensionelle rum, der omgiver den, med cylindriske bølgefronter..
Sfæriske bølger
Når kilden er punkt, og mediet, i hvilket den tredimensionelle bølge formerer sig, er homogent og isotrop (dets egenskaber ændres ikke i henhold til retningen), så er bølgefronterne kugler koncentriske til det punkt, hvor den oprindelige forstyrrelse opstod..
I tilfælde af en sfærisk bølge, hvor intensiteten af bølgen er identisk i alle retninger, afhænger funktionen, der beskriver forstyrrelsen, kun af afstanden r til punktkilden og tidspunktet t.
I dette tilfælde har vi, at den tilsvarende laplacian er:
∇tog = (1 / rto) ∂r(rto ∂rg)
At være bølge ligningen:
∇tog = (1 / volto) ∂ttg
Den generelle løsning ville være:
g (r, t) = (1 / r) F (r - v⋅t) + (1 / r) G (r + v⋅t)
I dette tilfælde siges det, at det er en sfærisk bølge. Men der kan være varianter, som det vil ses nedenfor
Ikke-isotrope sfæriske bølger
Det kan også ske, at en sfærisk bølge, det vil sige med bølgefronterne dannet af sfærer koncentrisk til et centralt punkt, er bølgens amplitude eller intensitet forskellig i de forskellige retninger..
Dette er, hvad der sker, når den centrale kilde til bølgen er mere effektiv i en retning end andre..
For eksempel har lyden, der produceres af en højttaler, ikke den samme intensitet overalt, selv ikke på punkter, der er lige langt fra højttaleren..
Intensiteten er ikke den samme, selvom signalet tager samme tid at nå disse punkter. Det er en sfærisk bølge, der har et ikke-sfærisk retningsmønster.
Du har også sfæriske bølger i tilfælde af elektromagnetiske bølger oprettet af en antenne, men de er muligvis ikke lige så stærke i alle retninger..

Inhomogent medium
Når mediet er inhomogent, er bølgens forplantningshastighed forskellig i forskellige retninger.
Et eksempel på et inhomogent medium er atmosfæren, hvor der er trykforskelle med højden, og der er temperaturgradienter. Et andet eksempel er lag af jordskorpen, som adskiller sig i tæthed og elastisk modul..
Ikke-homogeniteten resulterer i, at bølgefronterne, der stammer fra en central punktkilde, ikke er koncentriske sfærer, da afstanden, som bølgen har tilbagelagt i samme tidsperiode, er forskellig i hver retning..
Så har vi en tredimensionel bølge, hvis bølgefront ikke er sfærisk.
Intensitet og energi af en sfærisk bølge
Vi kan skrive udtrykket af en sfærisk harmonisk bølge som denne:
g (r, t) = (geller / r) cos (k⋅r - ω⋅t)
Hvor bølgefronterne formeres med radial hastighed svarende til:
v = ω / k
Og dens amplitude falder med afstandens omvendte retning r fra punktkilden til sfæriske bølger.
Harmoniske bølger har energitæthed (energi pr. enhedsvolumen) ε givet af:
ε = ½ ρ ωto (geller / r)to
I denne ligning:
-ρ har masseenheder pr. volumenhed og repræsenterer densiteten af mediet, hvor en lydbølge udbredes.
-geller er amplituden af forskydningen af et element i mediet, for eksempel et fluid, på grund af den formerende bølge.
Det skal bemærkes, at da det er en sfærisk bølge, falder energitætheden med det inverse af afstandens firkant.
Intensiteten af bølgen, det vil sige den transmitterede energi pr. Tidsenhed er:
I = v⋅ε
Som altid er den vigtigste mængde den transmitterede effekt pr. Arealenhed i radial afstand i praksis. r:
P = v⋅ε = Ieller / rto
At være jegeller = ½ ρ v ωto gellerto.
Den samlede energi, der transmitteres pr. Tidsenhed gennem en sfære med radius r er: P⋅4πrto= 4π⋅Ieller, og som forventet afhænger det ikke af den radiale afstand.
Eksempler på tredimensionelle bølger
Tredimensionelle bølger er meget hyppige, så vi har:
Elektromagnetiske bølger, der udsender antenner

De dækker et meget bredt spektrum, fra radiobølger mellem hundreder af KHz og hundreder af MHz til de bølger, der udsendes af antennen til trådløst internet i størrelsesordenen GHz, som allerede falder inden for mikrobølgeovnen.
Vi ved, at mikrobølger, selvom de ikke er ioniserende, er i stand til at øge kroppens temperatur, fordi den indeholder meget vand.
Derfor anbefales det ikke at have wi-fi-antennen tæt på hovedet eller kroppen. Det er nok at bevæge sig lidt væk, da intensiteten er den fjerde del ved dobbelt afstand.
Seismiske bølger
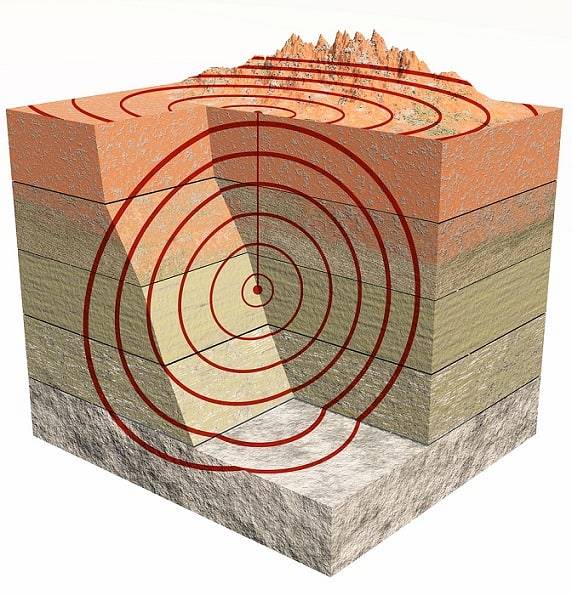
De er også tredimensionelle bølger. Hovedsagelig er der typen P hvad er kompressionsbølger og de af typen S som er klipning eller klipning (er)høre på engelsk).
Bølgerne P eller primærvalg er de første, der ankommer, fordi de formerer sig hurtigere end bølger S eller sekundær.
Lyd

Lyd er en type tredimensionel bølge. Disse bølger spredes i alle retninger, skønt, som vi har sagt før, ikke med den samme intensitet i alle retninger..
Dette skyldes, at lydkilden ikke altid udsender perfekt sfærisk symmetri.
Referencer
- Baranek, L. 1969. Akustik. 2. plads Udgave. Mcgraw bakke.
- Griffiths G. Lineære og ikke-lineære bølger. Gendannet fra: scholarpedia.org.
- Nottoli, H. 2004. Fysik anvendt på arkitektur. Nobuko.
- Whitham G.B. 1999. Lineære og ikke-lineære bølger. Wiley.
- Wikiwaves. Ikke-lineære bølger. Gendannet fra: wikiwaves.org


Endnu ingen kommentarer