
Newtons første lovformler, eksperimenter og øvelser
Det Newtons første lov, også kendt som lov om inerti, Det blev først foreslået af Isaac Newton, en engelsk fysiker, matematiker, filosof, teolog, opfinder og alkymist. Denne lov fastlægger følgende: “Hvis en genstand ikke udsættes for nogen kraft, eller hvis de kræfter, der virker på den, annullerer hinanden, vil den fortsætte med at bevæge sig med konstant hastighed i en lige linje. "
I denne erklæring er nøgleordet fortsættes. Hvis lovens forudsætninger er opfyldt, fortsætter objektet med dets bevægelse som det havde gjort. Medmindre en ubalanceret kraft vises og ændrer bevægelsestilstanden.
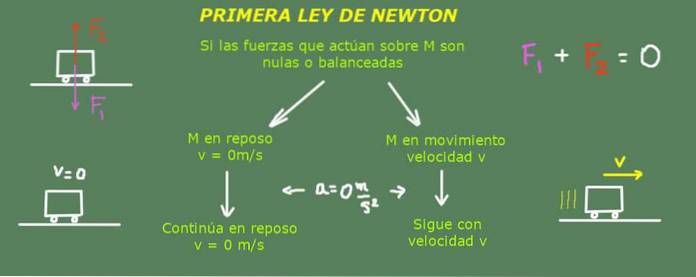
Dette betyder, at hvis objektet er i ro, vil det fortsætte med at hvile, undtagen hvis en kraft tager det ud af denne tilstand. Det betyder også, at hvis en genstand bevæger sig med en fast hastighed i en lige retning, vil den fortsætte med at bevæge sig på den måde. Det vil kun ændre sig, når en ekstern agent udøver en kraft på den og ændrer dens hastighed..
Artikelindeks
- 1 Lovens baggrund
- 2 Den før-newtonske opfattelse
- 3 Eksperimenter med inerti
- 3.1 Eksperiment 1
- 3.2 Eksperiment 2
- 3.3 Eksperiment 3
- 4 Forklaring til Newtons første lov
- 4.1 Træghed og masse
- 4.2 Eksempel
- 4.3 Inertialreferencesystem
- 4.4 Newtons første lov (inertilov)
- 5 Øvelser løst
- 5.1 Øvelse 1
- 5.2 Øvelse 2
- 6 Artikler af interesse
- 7 Referencer
Lovens baggrund
Isaac Newton blev født i Woolsthorpe Manor (Storbritannien) den 4. januar 1643 og døde i London i 1727.
Den nøjagtige dato, hvor Sir Isaac Newton opdagede sine tre dynamiske love, inklusive den første lov, er ikke kendt med sikkerhed. Men det vides, at det var længe før udgivelsen af den berømte bog Matematiske principper for naturfilosofi, 5. juli 1687.
Ordbogen for Det Kongelige Spanske Akademi definerer ordet inerti som følger:
"Ejendom af kroppe til at opretholde deres hvile eller bevægelse, hvis ikke ved hjælp af en styrke".
Dette udtryk bruges også til at bekræfte, at enhver situation forbliver uændret, fordi der ikke er gjort en indsats for at opnå det, derfor har ordet inerti undertiden en konnotation af rutine eller dovenskab..
Den før-newtonske opfattelse
Før Newton var de fremherskende ideer dem fra den store græske filosof Aristoteles, der sagde, at for at et objekt skal bevæge sig, skal en styrke handle på det. Når styrken ophører, så vil bevægelsen også gøre det. Det er ikke sådan, men selv i dag tror mange det.
Galileo Galilei, en strålende italiensk astronom og fysiker, der boede mellem 1564 og 1642, eksperimenterede og analyserede kroppens bevægelse.
En af Galileos observationer var, at en krop, der glider på en glat og poleret overflade med en bestemt indledende impuls, tager længere tid at stoppe og har større bevægelse i en lige linje, da friktionen mellem kroppen og overfladen er mindre.
Det er tydeligt, at Galileo håndterede tanken om inerti, men han kom ikke til at formulere en erklæring så præcis som Newton.
Nedenfor foreslår vi nogle enkle eksperimenter, som læseren kan udføre og bekræfte resultaterne. Observationer vil også blive analyseret i henhold til den aristoteliske vision om bevægelse og den newtonske vision..
Inerti eksperimenter
Eksperiment 1
En kasse fremdrives på gulvet, og derefter ophænges drivkraften. Vi bemærker, at kassen kører en kort sti, indtil den stopper.
Lad os fortolke det forrige eksperiment og dets resultat inden for rammerne af teorierne før Newton og derefter i henhold til den første lov.
I den aristoteliske vision var forklaringen meget klar: kassen stoppede, fordi den kraft, der flyttede den, blev suspenderet.
I den newtonske opfattelse kan kassen på gulvet / jorden ikke fortsætte med at bevæge sig med den hastighed, den havde i det øjeblik, kraften blev hængt op, fordi der mellem gulvet og kassen er en ubalanceret kraft, som får hastigheden til at falde, indtil boksestop. Det handler om friktionskraften.
I dette eksperiment opfyldes forudsætningerne for Newtons første lov ikke, så kassen stoppede.
Eksperiment 2
Igen er det kassen på gulvet / jorden. Ved denne mulighed opretholdes kraften på kassen på en sådan måde, at den kompenserer eller afbalancerer friktionskraften. Dette sker, når vi får kassen til at følge med konstant hastighed og i lige retning.
Dette eksperiment modsiger ikke det aristoteliske syn på bevægelse: kassen bevæger sig med konstant hastighed, fordi der udøves en kraft på den.
Det modsiger heller ikke Newtons tilgang, da alle de kræfter, der virker på kassen, er afbalancerede. Lad os se:
- I vandret retning er den kraft, der udøves på kassen, lig og i den modsatte retning af friktionskraften mellem kassen og gulvet.
- Så nettokraften i vandret retning er nul, derfor opretholder boksen sin hastighed og retning.
Også i lodret retning er kræfterne afbalanceret, fordi vægten af kassen, som er en kraft, der peger lodret nedad, kompenseres nøjagtigt af den kontaktkraft (eller normale) kraft, som jorden udøver på kassen lodret opad..
Forresten skyldes vægten af kassen Jordens tyngdekraft.
Eksperiment 3
Vi fortsætter med kassen hviler på gulvet. I den lodrette retning er kræfterne afbalanceret, det vil sige, den lodrette nettokraft er nul. Det ville helt sikkert være meget overraskende, hvis kassen flyttede opad. Men i vandret retning er der friktionskraft.
For at forudsætningen for Newtons første lov skal opfyldes, er vi nu nødt til at reducere friktion til dets mindste udtryk. Vi kan opnå dette på en forholdsvis tilnærmet måde, hvis vi ser efter en meget glat overflade, som vi sprøjter silikoneolie på.
Da silikoneolie reducerer friktionen til næsten nul, så når denne kasse kastes vandret, vil den bevare sin hastighed og retning i en lang strækning.
Det er det samme fænomen, der opstår med en skater på en skøjtebane eller med ishockeyspucken, når de fremdrives og frigives på egen hånd..
I de beskrevne situationer, hvor friktionen reduceres næsten til nul, er den resulterende kraft praktisk talt nul, og objektet opretholder sin hastighed ifølge Newtons første lov.
I den aristoteliske opfattelse kunne dette ikke ske, for ifølge denne naive teori finder bevægelse kun sted, når der er en nettokraft på det bevægelige objekt..

Newtons første lovforklaring
Træghed og masse
Masse er en fysisk størrelse, der angiver mængden af stof, som en krop eller genstand indeholder.
Masse er derefter en iboende egenskab af materie. Men stof består af atomer, der har masse. Atommassen er koncentreret i kernen. Det er protonerne og neutronerne i kernen, der praktisk talt definerer atomets og materiens masse..
Masse måles generelt i kg (kg), det er basisenheden i det internationale system for enheder (SI).
Prototypen eller referencen på kg er en platin- og iridiumcylinder, der opbevares i Det Internationale Kontor for Vægte og Foranstaltninger i Sèvres i Frankrig, selvom den i 2018 var knyttet til Planck-konstanten, og den nye definition træder i kraft fra 20. maj 2019.
Nå, det sker, at inerti og masse er relateret. Jo større masse, jo større inerti har et objekt. Det er meget vanskeligere eller dyrere med hensyn til energi at ændre bevægelsestilstanden for et mere massivt objekt end et mindre massivt..
Eksempel
For eksempel tager det meget mere kraft og meget mere arbejde at løfte en ton (1000 kg) kasse fra hvile end en 1 kg (1 kg) kasse. Derfor siges det ofte, at den første har mere inerti end den anden.
På grund af forholdet mellem inerti og masse indså Newton, at hastighed alene ikke er repræsentativ for bevægelsestilstanden. Derfor definerede han en mængde kendt som momentum eller momentum som er betegnet med brevet s y er massens produkt m for hastighed v:
s = m v
Den fed i s og i v angive, at de er vektor fysiske størrelser, det vil sige, de er størrelser med størrelse, retning og sans.
I stedet massen m er en skalar størrelse, hvortil der tildeles et tal, der kan være større end eller lig med nul, men aldrig negativt. Indtil videre er der ikke fundet noget objekt med negativ masse i det kendte univers..
Newton tog sin fantasi og abstraktion til det ekstreme og definerede kaldet fri partikel. En partikel er et materielt punkt. Det vil sige, det er som et matematisk punkt, men med masse:
En fri partikel er den partikel, der er så isoleret, så langt fra en anden genstand i universet, at intet kan udøve nogen interaktion eller kraft på den.
Senere fortsatte Newton med at definere inertialreferencesystemerne, som vil være dem, hvor hans tre bevægelseslove finder anvendelse. Her er definitionerne i henhold til disse begreber:
Træghedsreferencesystem
Ethvert koordinatsystem, der er knyttet til en fri partikel, eller som bevæger sig med konstant hastighed i forhold til den frie partikel, vil være et inertialreferencesystem.
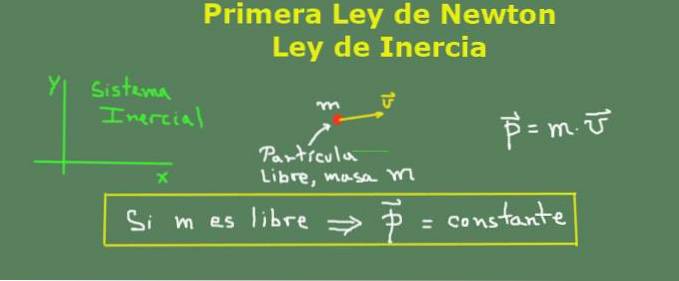
Newtons første lov (lov om inerti)
Hvis en partikel er fri, har den konstant momentum i forhold til en inerti-referenceramme.
Løst øvelser
Øvelse 1
En hockeyspuck på 160 gram går på skøjtebanen i 3 km / t. Find dit momentum.
Opløsning
Diskens masse i kg er: m = 0.160 kg.
Hastighed i meter over sekund: v = (3 / 3,6) m / s = 0,8333 m / s
Mængden af bevægelse eller momentum p beregnes som følger: p = m * v = 0,1333 kg * m / s,
Øvelse 2
Friktionen i den forreste skive betragtes som nul, så momentum bevares, så længe intet ændrer skivens lige forløb. Det er imidlertid kendt, at to kræfter virker på skiven: skivens vægt og den kontakt eller normale kraft, som gulvet udøver på den..
Beregn værdien af den normale kraft i newton og dens retning.
Opløsning
Da momentum er bevaret, skal den resulterende kraft på hockeyspucken være nul. Vægten peger lodret nedad og er gyldig: P = m * g = 0,16 kg * 9,81 m / s²
Den normale kraft skal nødvendigvis modvirke vægten, så den skal pege lodret opad, og dens størrelse vil være 1,57 N.
Artikler af interesse
Eksempler på Newtons lov i det virkelige liv.
Referencer
- Alonso M., Finn E. Fysik bind I: Mekanik. 1970. Fondo Educativo Interamericano S.A.
- Hewitt, P.. Konceptuel fysik. Femte udgave. Pearson. 67-74.
- Unge, Hugh. Universitetsfysik med moderne fysik. 14. udgave. Pearson. 105 - 107.


Endnu ingen kommentarer