
Lineær programmering, hvad det er til, modeller, begrænsninger, applikationer
Det lineær programmering er en matematisk metode, der bruges til at optimere (maksimere eller minimere efter behov) en funktion, hvis variabler er underlagt begrænsninger, så længe funktionen og begrænsningerne er lineært afhængige af variablerne.
Generelt er den funktion, der skal optimeres, en praktisk situation, såsom overskuddet fra en producent, hvis input, arbejdskraft eller maskiner er begrænsede.

Et af de enkleste tilfælde er, at en lineær funktion skal maksimeres, hvilket kun afhænger af to kaldte variabler beslutningsvariabler. Det kan have formen:
Z = k1x + ktoY
Med k1 og kto konstant. Denne funktion kaldes Objektiv funktion. Selvfølgelig er der situationer, der fortjener mere end to variabler til undersøgelse, idet de er mere komplekse:
Z = k1x1 + ktoxto + k3x3 +... .
Og begrænsningerne er også matematisk modelleret af et system af ligninger eller uligheder, lige lineære i x og Y.
Sættet med løsninger til dette system kaldes gennemførlige løsninger eller mulige punkter. Og blandt de mulige punkter er der mindst én, der optimerer den objektive funktion.
Lineær programmering blev uafhængigt udviklet af den amerikanske fysiker og matematiker George Dantzig (1914-2005) og den russiske matematiker og økonom Leonid Kantorovich (1912-1986) kort efter 2. verdenskrig..
Fejlfindingsmetoden kendt som simplex metode Det er hjernebarnet til Dantzig, der arbejdede for US Air Force, University of Berkeley og Stanford University.

Artikelindeks
- 1 Lineære programmeringsmodeller
- 2 Modeleksempel
- 3 Løsningsmetoder
- 3.1 - Grafisk eller geometrisk metode
- 3.2 - Dantzigs simplex-metode
- 4 applikationer
- 5 Øvelser løst
- 5.1 - Øvelse 1
- 5.2 - Øvelse 2
- 6 Referencer
Lineære programmeringsmodeller
De nødvendige elementer til etablering af en lineær programmeringsmodel, der er egnet til en praktisk situation, er:
-Objektiv funktion
-Beslutningsvariabler
-Begrænsninger
I objektivfunktionen definerer du, hvad du vil opnå. Antag for eksempel, at du vil maksimere din fortjeneste ved fremstilling af visse produkter. Derefter etableres "profit" -funktionen i henhold til den pris, som produkterne sælges til.
I matematiske termer kan denne funktion udtrykkes forkortet ved hjælp af summeringsnotationen:
Z = ∑kjeg xjeg
I denne ligning kjeg er koefficienter og xjeg er beslutningsvariablerne.
Beslutningsvariablerne er elementerne i systemet, hvis kontrol er haft, og deres værdier er positive reelle tal. I det foreslåede eksempel er beslutningsvariablerne mængden af hvert produkt, der skal fremstilles for at opnå den maksimale fortjeneste.
Endelig har vi begrænsningerne, som er lineære ligninger eller uligheder med hensyn til beslutningsvariabler. De beskriver begrænsningerne i problemet, som er kendte og kan for eksempel være de mængder råmateriale, der er tilgængelige under fremstillingen..
Typer af begrænsninger
Du kan have M antal begrænsninger startende fra j = 1 så længe j = M. Matematisk er begrænsningerne af tre typer:
- TILj = ∑ aij . xjeg
- Bj ≥ ∑ bij . xjeg
- Cj ≤ ∑ cij . xjeg
Den første begrænsning er af den lineære ligningstype og betyder, at værdien Aj, som er kendt, skal respekteres.
De resterende to begrænsninger er lineære uligheder, og det betyder, at B-værdiernej og Cj, kendt, kan de respekteres eller overskrides, når det viste symbol er ≥ (større end eller lig med) eller respekteres eller ikke overskrides, hvis symbolet er ≤ (mindre end eller lig med).
Modeleksempel
Anvendelsesområderne er meget forskellige, lige fra forretningsadministration til ernæring, men for at forstå metoden foreslås nedenfor en simpel model af en praktisk situation med to variabler..
En lokal konditori er kendt for to specialiteter: sortskovskagen og sacripantina-kagen..
Ved forberedelsen kræver de æg og sukker. Til sortskoven har du brug for 9 æg og 500 g sukker, mens du til sacripantine har brug for 8 æg og 800 g sukker. De respektive salgspriser er $ 8 og $ 10.
Problemet er: Hvor mange kager af hver type skal kagerne fremstille for at maksimere overskuddet, vel vidende at det har 10 kilo sukker og 144 æg?
Beslutningsvariabler
Beslutningsvariablerne er "x" og "y", som tager reelle værdier:
-x: antallet af sorte skovkager
-og: sacripantina kager.
Begrænsninger
Begrænsningerne er givet af det faktum, at antallet af kager er en positiv mængde, og at der er begrænsede mængder råmateriale til at forberede dem..
Derfor, i matematisk form, har disse begrænsninger form:
- x ≥ 0
- og ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Begrænsninger 1 og 2 udgør ikke-negativitetstilstand tidligere eksponeret, og alle de uligheder, der er rejst, er lineære. I begrænsning 3 og 4 er de værdier, der ikke må overskrides: 144 æg og 10 kg sukker.
Objektiv funktion
Endelig er den objektive funktion den fortjeneste, der opnås ved fremstilling af "x" -mængden af sorte skovkager plus "y" -mængden af sacripantiner. Den er bygget ved at multiplicere prisen med mængden af kager lavet og tilføje for hver type. Det er en lineær funktion, som vi kalder G (x, y):
G = 8x + 10 år
Løsningsmetoder
De forskellige løsningsmetoder inkluderer grafiske metoder, simpleksalgoritmen og den indre punktmetode for at nævne nogle få..
- Grafisk eller geometrisk metode
Når du har et to-variabelt problem som det i det foregående afsnit, bestemmer begrænsningerne et polygonal område i planet xy, opkald gennemførlig region eller levedygtighedsregion.
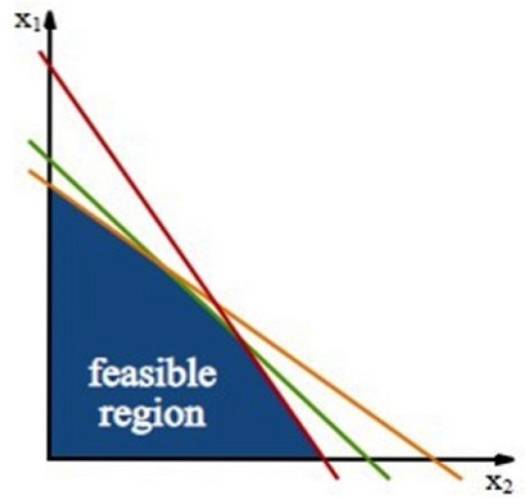
Denne region er bygget ved hjælp af begrænsningslinjer, hvilke linjer er opnået fra ulighederne mellem begrænsningerne, der kun arbejder med ligestillingstegnet.
For bageriet, der ønsker at optimere overskuddet, er begrænsningslinjerne:
- x = 0
- y = 0
- 9x + 8y = 144
- 0,5 x + 0,8 y = 10
Alle punkter i regionen lukket af disse linjer er mulige løsninger, så der er uendeligt mange af dem. Bortset fra i det tilfælde, hvor det mulige område viser sig at være tomt, i hvilket tilfælde det stillede problem ikke har nogen løsning.
Heldigvis er det mulige område for konditorproblemet ikke tomt, vi har det nedenfor.
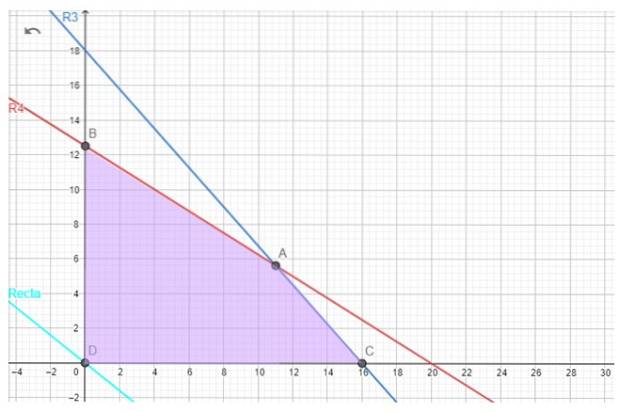
Den optimale løsning, hvis den findes, findes ved hjælp af den objektive funktion. For eksempel, når vi prøver at finde den maksimale forstærkning G, har vi følgende linje, der kaldes iso-profit-linje:
G = k1x + ktoy → y = -k1x / kto + G / kto
Med denne linje opnår vi alle parene (x, y), der giver en given forstærkning G, så der er en familie af linjer efter værdien af G, men alle med samme hældning -k1 / kto, så de er parallelle linjer.
Den optimale løsning
Nu kan det vises, at den optimale løsning på et lineært problem altid er et ekstremt punkt eller toppunkt i det mulige område. Derefter:
Løsningslinjen er den længst væk fra oprindelsen og har mindst et punkt til fælles med det mulige område.
Hvis linjen tættest på oprindelsen har et helt segment til fælles med den mulige region, siges det, at der er uendelige løsninger. Denne sag opstår, hvis hældningen af iso-profit-linjen er lig med en af de andre linjer, der begrænser regionen.
For vores wienerbrød er kandidatens hjørner A, B og C.
- Dantzigs simplex-metode
Den grafiske eller geometriske metode kan anvendes i to variabler. Det er dog mere kompliceret, når der er tre variabler og umuligt at bruge til et større antal variabler..
Når man beskæftiger sig med problemer med mere end to variabler, simplex metode, som består af en række algoritmer til at optimere de objektive funktioner. Matricer og enkel aritmetik bruges ofte til at udføre beregningerne.
Simplex-metoden begynder med at vælge en mulig løsning og kontrollere, om den er optimal. Hvis det er tilfældet, har vi allerede løst problemet, men hvis det ikke er tilfældet, fortsætter vi mod en løsning tættere på optimering. Hvis løsningen findes, finder algoritmen den i nogle få forsøg.
Ansøgninger
Lineær og ikke-lineær programmering anvendes på mange områder for at træffe de bedste beslutninger med hensyn til at reducere omkostninger og øge overskuddet, hvilket ikke altid er monetært, da de f.eks. Kan måles i tid, hvis du vil minimere den nødvendige tid at udføre en række operationer.
Her er nogle felter:
-Ved markedsføring bruges det til at finde den bedste kombination af medier (sociale netværk, tv, presse og andre) til at annoncere for et bestemt produkt.
-Til tildeling af passende opgaver til personalet i en virksomhed eller fabrik eller planlægning for dem.
-Ved udvælgelsen af den mest nærende mad og til de laveste omkostninger i husdyr- og fjerkræindustrien.
Løst øvelser
- Øvelse 1
Løs grafisk den lineære programmeringsmodel, der er rejst i de foregående afsnit.
Opløsning
Det er nødvendigt at tegne et sæt værdier bestemt af det begrænsningssystem, der er angivet i problemet:
- x ≥ 0
- og ≥0
- 9x + 8y ≤ 144
- 0,5 x + 0,8 y ≤ 10
Regionen givet ved ulighed 1 og 2 svarer til den første kvadrant i det kartesiske plan. Med hensyn til ulighed 3 og 4 begynder vi med at finde begrænsningslinjerne:
9x + 8y = 144
0,5 x + 0,8 år = 10 → 5 x + 8 år = 100
Det mulige område er en firkant, hvis hjørner er punkterne A, B, C og D..
Minimumsgevinsten er 0, derfor er linjen 8x + 10y = 0 den nedre grænse, og iso-profitlinjerne har hældning -8/10 = - 0,8.
Denne værdi er forskellig fra hældningerne på de andre begrænsningslinjer, og da den mulige region er afgrænset, findes den unikke løsning.
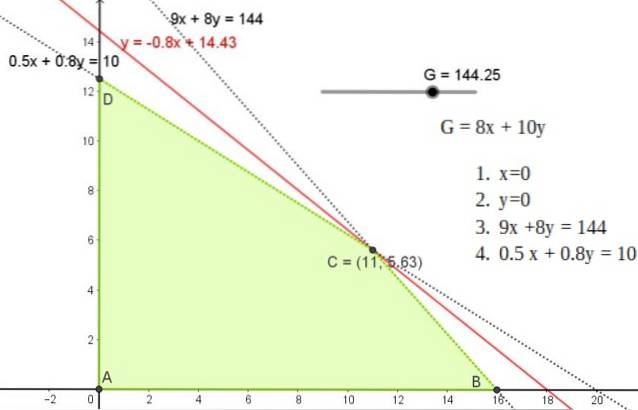
Denne løsning svarer til en linje med hældning -0.8, der passerer gennem et af punkterne A, B eller C, hvis koordinater er:
A (11; 5,625)
B (0; 12,5)
C (16, 0)
Optimal løsning
Vi beregner værdien af G for hvert af disse punkter:
-(11; 5,625): GTIL = 8 x 11 + 10 x 5,625 = 144,25
-(0; 12,5): GB = 8 x 0 + 10 x 12,5 = 125
-(16, 0): GC = 8 x 16 + 10 x 0 = 128
Den største fortjeneste findes ved at fremstille 11 sorte skovkager og 5.625 sakripantinkager. Denne løsning matcher den, der findes gennem softwaren.
- Øvelse 2
Bekræft resultatet af den foregående øvelse ved hjælp af Solver-funktionen, der er tilgængelig i de fleste regneark, såsom Excel eller LibreOffice Calc, som indeholder Simplex-algoritmen til optimering i lineær programmering.
Opløsning
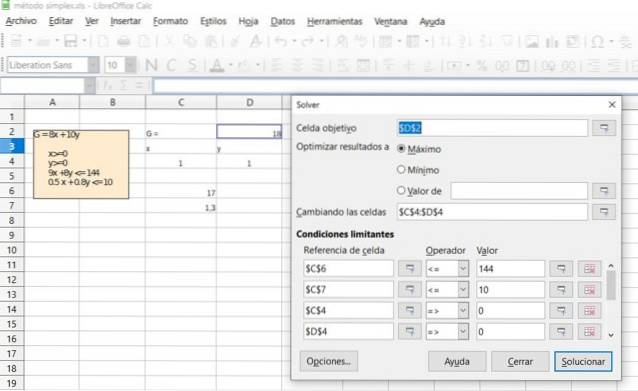
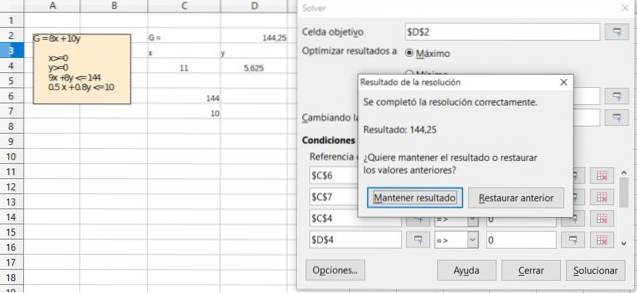
Referencer
- Strålende. Lineær programmering. Gendannet fra: brilliant.org.
- Eppen, G. 2000. Operations Research in Administrative Science. 5. plads Udgave. Prentice hall.
- Haeussler, E. 1992. Matematik til ledelse og økonomi. 2. plads Udgave. Grupo Editorial Iberoamericana.
- Hiru.eus. Lineær programmering. Gendannet fra: hiru.eus.
- Wikipedia. Lineær programmering. Gendannet fra: es. wikipedia.org.


Endnu ingen kommentarer