
Associerende ejendomsaddition, multiplikation, eksempler, øvelser
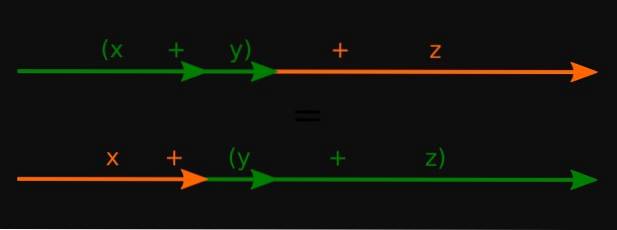
Det associerende ejendom af summen repræsenterer den associerende karakter af sumoperationen i forskellige matematiske sæt. I det er tre (eller flere) elementer i disse sæt beslægtede, kaldet a, b og c, således at det altid er sandt:
a + (b + c) = (a + b) + c
På denne måde er det garanteret, at resultatet er det samme, uanset hvordan gruppen grupperes for at udføre operationen.

Men det skal bemærkes, at den associerende egenskab ikke er synonym med kommutativ ejendom. Det vil sige, vi ved, at rækkefølgen af tilføjelserne ikke ændrer summen, eller at rækkefølgen af faktorer ikke ændrer produktet. Så for summen kan det skrives således: a + b = b + a.
Imidlertid er det i den associerende egenskab anderledes, da rækkefølgen af de elementer, der skal tilføjes, opretholdes, og hvilke ændringer der er den operation, der udføres først. Hvilket betyder, at det ikke betyder noget at tilføje først (b + c) og til dette resultat tilføje a, end at begynde at tilføje a med b og til resultatet tilføje c.
Mange vigtige operationer som tilføjelse er associerende, men ikke alle. For eksempel sker der i subtraktion af reelle tal, at:
a - (b - c) ≠ (a - b) - c
Hvis a = 2, b = 3, c = 1, så:
2- (3 - 1) ≠ (2-3) - 1
0 ≠ -2
Artikelindeks
- 1 Associerende egenskab ved multiplikation
- 1.1 Anvendelser af den associerende egenskab ved multiplikation
- 2 Eksempler
- 2.1 Den associerende egenskab i vektorer
- 2.2 Faktorisering af polynomer ved gruppering af termer
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Associerende egenskab ved multiplikation
Som det blev gjort for tilføjelse, angiver den associerende egenskab ved multiplikation, at:
a ˟ (b ˟ c) = (a ˟ b) ˟ c
I tilfælde af sættet med reelle tal er det let at kontrollere, at dette altid er tilfældet. For eksempel bruger værdierne a = 2, b = 3, c = 1, vi har:
to ˟ (3 ˟ 1) = (2 ˟ 3) ˟ 1 → 2 ˟ 3 = 6 ˟ 1
6 = 6
Reelle tal opfylder den associerende egenskab ved både addition og multiplikation. På den anden side er summen i et andet sæt, som for vektorer, associerende, men krydsproduktet eller vektorproduktet er det ikke..
Anvendelser af den associerende egenskab af multiplikation
En fordel ved operationer, hvor den associerende ejendom er opfyldt, er at kunne gruppere på den mest bekvemme måde. Dette gør opløsning meget lettere..
Antag for eksempel, at der i et lille bibliotek er 3 hylder med 5 hylder hver. I hver hylde er der 8 bøger. Hvor mange bøger er der i alt?
Vi kan udføre operationen således: samlede bøger = (3 x 5) x 8 = 15 x 8 = 120 bøger.
Eller sådan her: 3 x (5 x 8) = 3 x 40 = 120 bøger.

Eksempler
-I sæt af naturlige, heltal, rationelle, reelle og komplekse tal er den associerende egenskab af addition og multiplikation opfyldt.
-For polynomer gælder også i disse operationer.
-I tilfælde af operationer med subtraktion, opdeling og eksponentiering opfyldes den associerende ejendom hverken i reelle tal eller i polynomer.
-I tilfælde af matricer gælder den associerende egenskab for addition og multiplikation, selv om kommutativitet ikke er opfyldt i sidstnævnte tilfælde. Dette betyder, at det i betragtning af matricerne A, B og C er rigtigt, at:
(A x B) x C = A x (B x C)
Men ... A x B ≠ B x A
Den associerende egenskab i vektorer
Vektorer danner et andet sæt end reelle tal eller komplekse tal. De operationer, der er defineret for sæt af vektorer, er noget forskellige: der er addition, subtraktion og tre typer produkter.
Summen af vektorer opfylder den associerende egenskab, ligesom tal, polynomer og matricer. Hvad angår de skalære produkter, skalar efter vektor og kryds, der er lavet mellem vektorer, opfylder sidstnævnte det ikke, men det skalære produkt, som er en anden slags operation mellem vektorer, opfylder det dog under hensyntagen til følgende:
-Produktet af en skalar og en vektor resulterer i en vektor.
-Og når der skaleres multipliceret to vektorer, resulterer en skalar.
Derfor givet vektorerne v, eller Y w, og derudover en skalær λ, er det muligt at skrive:
-Summen af vektorer: v +(eller + w ) = (v + eller) + w
-Skalarprodukt: λ (v • eller ) = (λv) • eller
Sidstnævnte er mulig takket være v • eller resulterer i en skalar og λv det er en vektor.
Imidlertid:
v × (eller × w ) ≠ (v × eller)×w
Faktorisering af polynomer ved gruppering af termer
Denne applikation er meget interessant, for som det blev sagt før, hjælper den associerende egenskab med at løse visse problemer. Summen af monomier er associativ, og dette kan bruges til at faktorere, når en åbenbar fælles faktor ikke vises ved første øjekast.
Antag for eksempel, at du beder om at faktorere: x3 + toxto + 3x +6. Dette polynom har ingen fælles faktor, men lad os se, hvad der sker, hvis det er grupperet således:
x3 + 2xto + 3x +6 = (x3 + 2xto) + (3x +6)
Den første parentes har som en fælles faktor xto:
x3 + toxto = xto (x + 2)
I det andet er den fælles faktor 3:
3x +6 = 3 (x + 2)
Derefter:
x3 + toxto + 3x +6 = xto(x + 2) + 3 (x + 2)
Nu er der en indlysende fælles faktor, hvilket er x + 2:
xto(x + 2) + 3 (x + 2) = (x + 2) (xto+3)
Uddannelse
- Øvelse 1
En skolebygning har 4 etager og hver har 12 klasseværelser med 30 skriveborde indeni. Hvor mange skriveborde har skolen i alt?
Opløsning
Dette problem løses ved at anvende den associerende egenskab af multiplikation, lad os se:
Samlet antal skriveborde = 4 etager x 12 klasseværelser / etage x 30 skriveborde / klasselokale = (4 x 12) x 30 skriveborde = 48 x 30 = 1440 skriveborde.
Eller hvis du foretrækker det: 4 x (12 x 30) = 4 x 360 = 1440 skriveborde
- Øvelse 2
I betragtning af polynomierne:
A (x) = 5x3 + 2xto -7x + 1
B (x) = x4 +6x3 -5x
C (x) = -8xto +3x -7
Anvend den associerende egenskab ved tilføjelse for at finde A (x) + B (x) + C (x).
Opløsning
Du kan gruppere de to første og føje den tredje til resultatet:
A (x) + B (x) = [5x3 + 2xto -7x + 1] + [x4 +6x3 -5x] = x4 + 11x3+ 2xto -12x +1
Umiddelbart tilføjes polynomet C (x):
[x4 + 11x3+ 2xto -12x +1] + [-8xto +3x -7] = x4 + 11x3 - 6xto -9x -6
Læseren kan kontrollere, at resultatet er identisk, hvis det løses ved hjælp af indstillingen A (x) + [B (x) + C (x)].
Referencer
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematik er sjov Kommutativ, associerende og distribuerende lovgivning. Gendannet fra: mathisfun.com.
- Matematiklager. Definition af associeret ejendom. Gendannet fra: mathwarehouse.com.
- Videnskabelig. Associerende og kommutativ egenskab ved tilføjelse og multiplikation (med eksempler). Gendannet fra: sciencing.com.
- Wikipedia. Associeret ejendom. Gendannet fra: en.wikipedia.org.



Endnu ingen kommentarer