
Hvad er partiklens ligevægt? (Med eksempler)
Det partikel ligevægt Det er en tilstand, hvor en partikel findes, når de eksterne kræfter, der virker på dem, annulleres gensidigt. Dette forudsætter, at det opretholder en konstant tilstand på en sådan måde, at det kan forekomme på to forskellige måder afhængigt af den specifikke situation.
Den første er at være i statisk ligevægt, hvor partiklen er immobil; og det andet er den dynamiske ligevægt, hvor summen af kræfter annullerer, men alligevel har partiklen ensartet retlinet bevægelse.

Partikelmodellen er en meget nyttig tilnærmelse til at studere kroppens bevægelse. Det består i at antage, at hele kroppens masse er koncentreret i et enkelt punkt, uanset størrelsen på objektet. På denne måde kan du repræsentere en planet, en bil, en elektron eller en billardkugle.
Artikelindeks
- 1 Den resulterende kraft
- 2 diagrammer med fri krop
- 3 måder at anvende ligevægtsbetingelsen på
- 3.1 To kræfter af samme størrelse og modsat retning og retninger
- 3.2 To kræfter af forskellig størrelse, samme retning og modsatte retninger
- 3.3 To kræfter af samme størrelse og forskellig retning
- 3.4 Tre kræfter med forskellig retning
- 4 friktion
- 4.1 Den dynamiske friktion
- 5 Arbejdet eksempel
- 5.1 Løsning
- 6 Referencer
Den resulterende kraft
Det punkt, der repræsenterer objektet, er hvor de kræfter, der påvirker det, virker. Alle disse kræfter kan erstattes af en enkelt, der har den samme effekt, som kaldes resulterende kraft eller nettokraft og betegnes som FR eller FN.
Ifølge Newtons anden lov, når der er en ubalanceret resulterende kraft, oplever kroppen en acceleration, der er proportional med kraften:
FR = m.a
Hvor til er den acceleration, som objektet erhverver takket være kraftens og m er genstandens masse. Hvad sker der, hvis kroppen ikke accelereres? Præcis hvad der blev angivet i starten: kroppen er i ro eller bevæger sig med ensartet retlinjet bevægelse, som mangler acceleration.
For en partikel i ligevægt er det gyldigt at sikre, at:
FR = 0
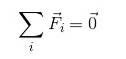
Da tilføjelse af vektorer ikke nødvendigvis indebærer tilføjelse af modulerne, skal vektorerne nedbrydes. Det er således gyldigt at udtrykke:
Fx = m.ax = 0; FY = m.aY = 0; Fz = m.az = 0
Diagrammer med fri krop
For at visualisere de kræfter, der virker på partiklen, er det praktisk at lave et fritlegemsdiagram, hvor alle de kræfter, der virker på objektet, er repræsenteret af pile..
Ovenstående ligninger er vektor af natur. Ved nedbrydning af kræfterne adskiller de sig ved tegn. På denne måde er det muligt for summen af dets komponenter at være nul.
Følgende er vigtige retningslinjer for at gøre tegningen nyttig:
- Vælg et referencesystem, hvor den største mængde kræfter er placeret på koordinatakserne.
- Vægt trækkes altid lodret ned.
- I tilfælde af to eller flere overflader i kontakt er der normale kræfter, som altid trækkes ved at skubbe kroppen og vinkelret på den overflade, der udøver den..
- For en partikel i ligevægt kan der være friktioner, der er parallelle med kontaktoverfladen og modsætter sig den mulige bevægelse, hvis partiklen betragtes som i hvile eller bestemt i modsætning, hvis partiklen bevæger sig med MRU (ensartet retlinet bevægelse).
- Hvis der er et reb, trækkes spændingen altid langs det og trækker kroppen.
Måder at anvende ligevægtsbetingelsen på
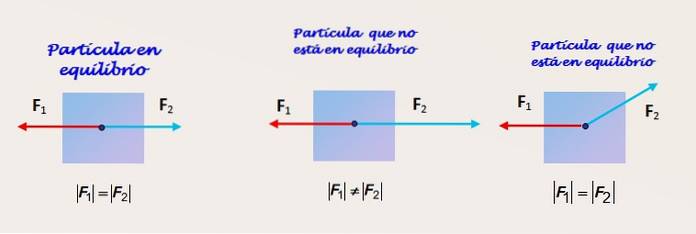
To kræfter af samme størrelse og modsat retning og retninger
Figur 2 viser en partikel, hvorpå to kræfter virker. I figuren til venstre modtager partiklen virkningen af to kræfter F1 og Fto der har samme størrelse og virker i samme retning og i modsatte retninger.
Partiklen er i ligevægt, men ikke desto mindre med de leverede oplysninger er det ikke muligt at vide, om ligevægten er statisk eller dynamisk. Flere oplysninger er nødvendige om den inertiale referenceramme, hvorfra objektet observeres.
To kræfter af forskellig størrelse, i samme retning og modsatte retninger
Figuren i midten viser den samme partikel, som denne gang ikke er i ligevægt, da størrelsen af kraften Fto er større end F1. Derfor er der en ubalanceret kraft, og objektet har en acceleration i samme retning som Fto.
To kræfter af samme størrelse og forskellig retning
Endelig ser vi i figuren til højre en krop, der heller ikke er i ligevægt. På trods af at F1 og Fto har samme størrelse, kraften Fto er ikke i samme retning som 1. Den lodrette komponent af Fto modvirkes ikke af nogen anden, og partiklen oplever en acceleration i den retning.
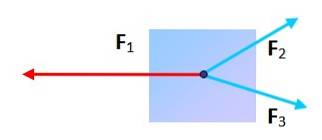
Tre kræfter med forskellig retning
Kan en partikel, der udsættes for tre kræfter, være i ligevægt? Ja, så længe når du placerer slutningen og slutningen af hver enkelt, er den resulterende figur en trekant. I dette tilfælde er vektorsummen nul.
Friktion
En kraft, der ofte griber ind i partiklens ligevægt, er statisk friktion. Det skyldes interaktionen mellem objektet repræsenteret af partiklen og overfladen af en anden. For eksempel er en bog i statisk ligevægt på et skråt bord modelleret som en partikel og har et frit legemsdiagram som følgende:
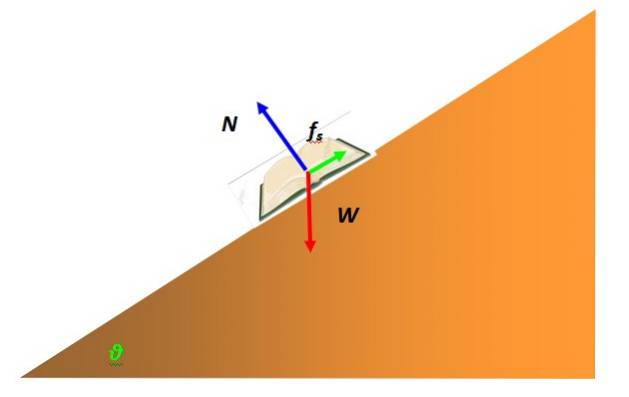
Den kraft, der forhindrer bogen i at glide over overfladen af det skrå plan og forblive i ro, er statisk friktion. Det afhænger af arten af overfladerne i kontakt, som mikroskopisk præsenterer ruhed med toppe, der går i indgreb med hinanden, hvilket gør bevægelse vanskelig..
Den maksimale værdi af statisk friktion er proportional med den normale kraft, den kraft, der udøves af overfladen på det understøttede objekt, men vinkelret på overfladen. I eksemplet i bogen er det angivet med blåt. Matematisk udtrykkes det således:
Fs mere∝ N
Konstanten af proportionalitet er statisk friktionskoefficient μs, som bestemmes eksperimentelt, er dimensionsløs og afhænger af arten af overfladerne i kontakt.
Fs maks = μs N
Den dynamiske friktion
Hvis en partikel er i dynamisk ligevægt, finder bevægelse allerede sted, og statisk friktion griber ikke længere ind. Hvis der er nogen friktionskraft, der modsætter bevægelsen, virker den dynamiske friktion, hvis størrelse er konstant og er givet ved:
Fk = μk N
Hvor μk er han dynamisk friktionskoefficient, Det afhænger også af typen af overflader, der er i kontakt. Ligesom den statiske friktionskoefficient er den dimensioneløs, og dens værdi bestemmes eksperimentelt.
Værdien af koefficienten for dynamisk friktion er normalt mindre end den for statisk friktion.
Arbejdet eksempel
Bogen i figur 3 er i ro og har en masse på 1,30 kg. Flyet har en hældningsvinkel på 30º. Find koefficienten for statisk friktion mellem bogen og den plane overflade.
Opløsning
Det er vigtigt at vælge et passende referencesystem, se følgende figur:
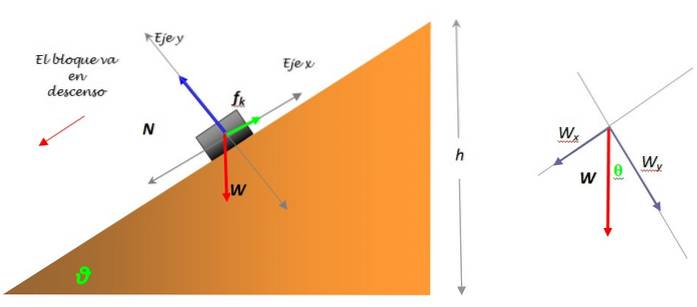
Vægten af bogen har størrelse W = mg, det er dog nødvendigt at opdele det i to komponenter: Wx Y WY, da det er den eneste kraft, der ikke falder lige over nogen af koordinatakserne. Nedbrydningen af vægten observeres i figuren til venstre.
WY = mg.cosθ = 1,30 x 9,8 x cos 30º N = 11,03 N
Wx = mg sinθ = 1,30 x 9,8 x sin 30º = 6,37 N
Den 2. Newtons lov for den lodrette akse er:
N - Wy = 0
N = mg. cos θ = 11,03 N.
Anvendelse af 2.. Newtons lov for x-aksen, der vælger retningen af den mulige bevægelse som positiv:
Wx - Fs = 0
Den maksimale friktion er Fs maks= μsN, Dermed:
Wx - μsN = 0
μs = Wx / N = 6,37 / 11,03 = 0,58
Referencer
- Rex, A. 2011. Grundlæggende fysik. Pearson. 76 - 90.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7mor. Ed. Cengage Learning. 120 - 124.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9na Ed. Cengage Learning. 99-112.
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. MacGraw Hill. 71 - 87.
- Walker, J. 2010. Fysik. Addison Wesley. 148-164.



Endnu ingen kommentarer