Hvad er lineær hastighed? (Med øvelser løst)

Det lineær hastighed det er defineret som det, der altid er tangentielt for den bane, der følges af partiklen, uanset dens form. Hvis partiklen altid bevæger sig i en retlinet sti, er der ikke noget problem at forestille sig, hvordan hastighedsvektoren følger denne lige linje.

Generelt udføres bevægelsen imidlertid på en vilkårligt formet kurve. Hver del af kurven kan modelleres som om den var en del af en cirkel med radius til, som på hvert punkt er tangent til den fulgte vej.

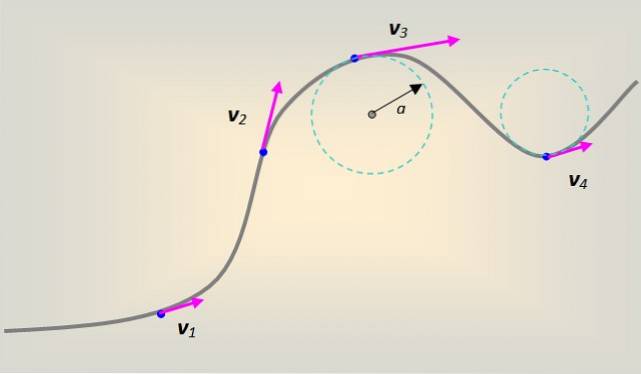
I dette tilfælde ledsager den lineære hastighed kurven tangentielt og til enhver tid på hvert punkt af den..

Matematisk er den øjeblikkelige lineære hastighed afledt af positionen i forhold til tid. Være r partikelens placeringsvektor på et øjeblik t, så er den lineære hastighed givet ved udtrykket:

v = r'(t) = dr / dt

Dette betyder, at den lineære hastighed eller tangentielle hastighed, som det ofte kaldes, ikke er andet end ændringen i position med hensyn til tid..

Artikelindeks

• 1 Lineær hastighed i cirkulær bevægelse
  • 1.1 Lineær hastighed, vinkelhastighed og centripetal acceleration
  • 1.2 -Løst øvelse 1 
  • 1.3 -Løst øvelse 2
• 2 Referencer

Lineær hastighed i cirkulær bevægelse

Når bevægelsen er på en omkreds, kan vi gå ved siden af ​​partiklen på hvert punkt og se, hvad der sker i to meget specielle retninger: en af ​​dem er den, der altid peger mod centrum. Dette er adressen radial.

Den anden vigtige retning er den, der passerer omkredsen, dette er retningen tangentiel og lineær hastighed har det altid.

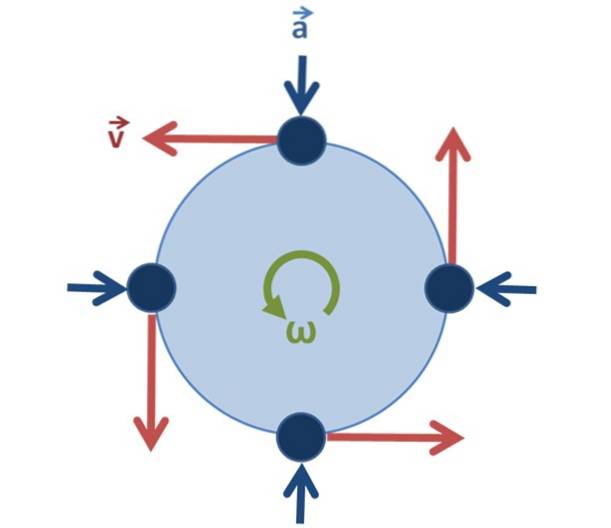
I tilfælde af ensartet cirkulær bevægelse er det vigtigt at indse, at hastigheden ikke er konstant, da vektoren ændrer sin retning, når partiklen roterer, men dens modul (størrelsen på vektoren), som er hastigheden, ja forbliver uændret.

Til denne bevægelse er positionen som funktion af tiden givet af s (t), hvor s er han bueløb Y t Det er tiden. I så fald er den øjeblikkelige hastighed givet af udtrykket v = ds / dt og det er konstant.

Hvis hastighedens størrelse også varierer (vi ved allerede, at retningen altid gør, ellers kunne mobilen ikke dreje), står vi over for en varieret cirkulær bevægelse, hvorunder mobilen ud over at dreje kan bremse eller accelerere.

Lineær hastighed, vinkelhastighed og centripetal acceleration

Partiklens bevægelse kan også ses fra synspunktet fejet vinkel, i stedet for at gøre det fra buegangen. I et sådant tilfælde taler vi om Vinkelhastighed. Til bevægelse på en radius af omkredsen R, der er et forhold mellem lysbue (i radianer) og vinkel:

s = R θ

Udledning med hensyn til tid på begge sider:

ds / dt = R (dθ/ dt)

At kalde afledningen af ​​θ med hensyn til t Hvad Vinkelhastighed og betegner det med det græske bogstav ω "omega", har vi dette forhold:

v = ωR

Centripetal acceleration

Al cirkulær bevægelse har centripetal acceleration, som altid er rettet mod centrum af omkredsen. Hun sørger for, at hastigheden ændres for at bevæge sig med partiklen, når den roterer.

Centripetal acceleration til_c eller til_R peger altid mod midten (se figur 2) og er relateret til lineær hastighed som denne:

til_c = v^to / R

Og med vinkelhastigheden som:

til_c = (ωR)^to / R = ω^toR

For ensartet cirkulær bevægelse, positionen s (t) er af formen:

s (t) = så + vt

Desuden skal den varierede cirkulære bevægelse have en komponent af acceleration kaldet tangentiel acceleration til_T, der beskæftiger sig med at ændre størrelsen på den lineære hastighed. Ja til_T  det er konstant, stillingen er:

s (t) = s_eller + v_ellert + ½ a_Tt^to

Med v_eller som starthastighed.

Løst problemer med lineær hastighed

De løste øvelser hjælper med at tydeliggøre korrekt brug af begreberne og ligningerne ovenfor..

-Løst øvelse 1 

Et insekt bevæger sig på en halvcirkel med radius R = 2 m, startende fra hvile ved punkt A, mens den øger sin lineære hastighed med en hastighed på p m / s^to. Find: a) Efter hvor længe det når punkt B, b) Den lineære hastighedsvektor i det øjeblik, c) Accelerationsvektoren på det øjeblik.

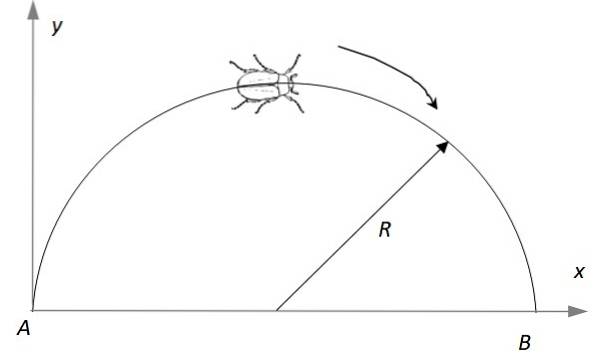
Opløsning

a) Erklæringen angiver, at den tangentielle acceleration er konstant og er lig med π m / s^to, så er det gyldigt at bruge ligningen til ensartet varieret bevægelse:

s (t) = s_eller + v_ellert + ½ a_T.t^to

Med s_eller = 0 og v_eller = 0:

s (t) = ½ a_T.t^to

s = πR (Halv længde af omkredsen)

t = (2. πR /til_T) ^½ s = (2π.2 / π)^½s = 2 s

b) v (t) = v_eller + til_T. t = 2π Frk

Når det er ved punkt B, peger den lineære hastighedsvektor i lodret retning nedad i retningen (-Y):

v (t) = 2π Frk(-Y)

c) Vi har allerede den tangentielle acceleration, den centripetale acceleration mangler for at have hastighedsvektoren til:

til_c = v^to / R = (2π)^to / 2 m / s^to = 2π^to Frk^to

til = a_c (-x) + a_T (-Y) = 2π^to(-x) + π (-Y) Frk^to

-Træning løst 2

En partikel roterer i en cirkel med en radius på 2,90 m. På et bestemt tidspunkt er dens acceleration 1,05 m / s^to i en sådan retning, at den danner 32º med sin bevægelsesretning. Find dens lineære hastighed ved: a) Dette øjeblik, b) 2 sekunder senere, forudsat at den tangentielle acceleration er konstant.

Opløsning

a) Bevægelsesretningen er netop den tangentielle retning:

til_T = 1,05 m / s^to . cos 32º = 0,89 m / s^to ; til_C = 1,05 m / s^to . sin 32º = 0,56 m / s^to

Hastigheden rydder fra til_c = v^to / R Hvad:

v = (R.a_c)^1/2  = 1,27 m / s

b) Følgende ligning er gyldig for ensartet varieret bevægelse: v = v_eller + til_Tt = 1,27 + 0,89,2^to m / s = 4,83 m / s

Referencer

1. Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 84-88.
2. Figueroa, D. Physics Series for Sciences and Engineering. Bind 3. Udgave. Kinematik. 199-232.
3. Giancoli, D. 2006. Fysik: Principper med applikationer. 6^th... Ed Prentice Hall. 62-64.
4. Relativ bevægelse. Gendannet fra: courses.lumenlearning.com
5. Wilson, J. 2011. Fysik 10. Pearson Education. 166-168.