Hvad er trekantede tal? Egenskaber og demonstrationer

Det er kendt som trekantede tal til rækkefølgen af ​​tal, der opnås ved at lave et arrangement eller et figurpoint i form af en ligesidet trekant. De første i sekvensen er: 1, 3, 6, 10, 15, 21, ...

Det første trekantede tal er 1, det andet er 3, fordi det opnås ved at tilføje en række med to punkter til den forrige for at danne en ligesidet trekant med tre elementer.

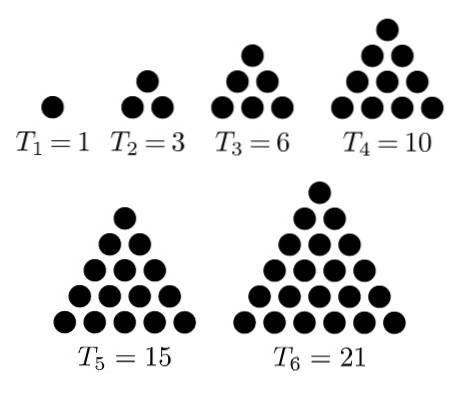
Den tredje er 6, som vises, når der tilføjes en række på tre punkter til det foregående arrangement på en sådan måde, at der dannes en trekant på tre punkter pr. Side. Sekvensen 10 opnås ved at tilføje en anden række til det foregående arrangement, så der dannes en trekant på fire punkter pr. Side.

Formlen, der gør det muligt at finde elementet n af den trekantede sekvens, kendt det foregående trekantede tal er:

T_n = T_n-1 + n

Listen over de første seks trekantede tal opnås således:

-Først: 1

-Sekund: 1 + 2 = 3

-Tredje: (1 +2) + 3 = 3 + 3 = 6

-Soveværelse: (1 + 2 + 3) + 4 = 6 + 4 = 10

-Femte: (1 + 2 + 3 + 4) + 5 = 10 + 5 = 15

-Sjette: (1 + 2 + 3 + 4 + 5) + 6 = 15 + 6 = 21

Artikelindeks

• 1 Egenskaber for trekantede tal
• 2 demonstrationer
  • 2.1 - Demo 1
  • 2.2 - Demo 2
  • 2.3 - Demo 3
  • 2.4 - Demonstration 5
• 3 Referencer

Egenskaber for trekantede tal

1.- Det n-th trekantede tal Tn i sekvensen af ​​trekantede tal er halvdelen af ​​n ganget med n + 1:

T_n = ½ n (n + 1)

2. - Summen af ​​det n-th trekantede tal med det forrige trekantede tal, dvs. (n-1) -th, er n kvadratisk:

T_n + T_n-1= n^to

3.- Forskellen i det n-th trekantede tal minus den n-th trekantede minus en er n:

T_n - T_n-1 = n

4. - Summen af ​​de første n trekantede tal kaldes det tetraedriske tal Sn og er lig med den sjette del af produktet af n ganget med (n + 1) og ganget med (n + 2):

S_n= ⅙ n (n + 1) (n + 2)

5.- Hvert naturligt tal N er resultatet af summen af ​​tre trekantede tal:

N = A1 + A1 + A3

Denne sidste ejendom eller sætning blev opdaget af den store matematiker Carl Friedrich Gauss i 1796, som han bemærkede i sin dagbog og placerede den græske beundring Eureka! hvad betyder det "Jeg har gjort det".

Det var det samme ord, der blev brugt længe før af den græske Archimedes, da han bestemte den tilsyneladende vægt af en nedsænket krop..

I dette forhold tages tallet nul som trekantet, og der kan være gentagelse.

Demonstrationer

- Demo 1

Bevis, at det trekantede tal n-det her:

T_n = ½ n (n + 1)

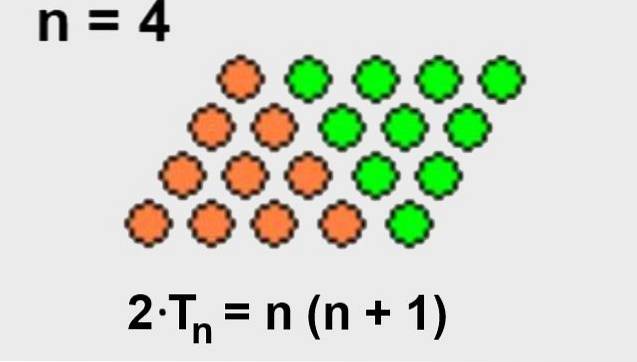
Det er let at udlede ovenstående formel, hvis vi indser, at vi kan tilføje et lige antal point til det trekantede arrangement, så det danner en firkant af punkter.

Da det samlede antal point i det firsidede arrangement er antallet af rækker n ganget med antallet af kolonner (n + 1), så vil det trekantede arrangement kun have halvdelen af ​​punkterne i det firkantede arrangement.

Her er det illustreret i figur 2.

- Demo 2

Vis, at summen af n-trekantsnummer med n-th minus en trekantet tal er n kvadratisk:

T_n + T_n-1= n^to

Det er allerede vist, at det trekantede tal n-th er givet af:

T_n= ½ n (n + 1)

Derfor er det trekantede tal ovenfor:

T_n-1 = ½ (n-1) ((n-1) + 1) = ½ n (n - 1)

Summen af ​​begge er:

T_n + T_n-1 = ½ n (n + 1) + ½ n (n - 1)

Den fælles faktor ½ n tages for at opnå:

T_n + T_n-1 = ½ n [(n + 1) + (n - 1)] = ½ n [n + 1 + n - 1]

Og straks forenkles udtrykket inden i beslaget:

T_n + T_n-1 = ½ n [2 n] = ½ 2 n ⋅ n

Husk nu, at ½ gange 2 er 1, og at n gange n er n i kvadrat, har vi:

T_n + T_n-1 = n^to

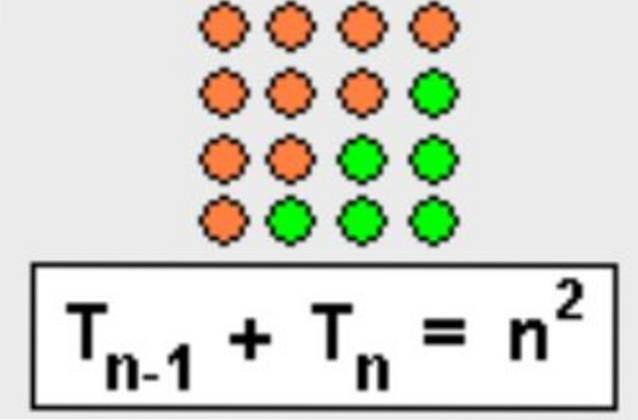
Denne egenskab kan også demonstreres i geometrisk form, udfyld blot trekanten for at danne en firkant, som vist i figur 3.

- Demo 3

Forskellen på det trekantede ordrenummer n minus det trekantede ordrenummer n-1 er n:

T_n - T_n-1 = n

Dette kan bevises ved simpelthen at huske, at følgende trekantede tal opnås fra det foregående ved hjælp af formlen:

T_n = T_n-1 + n

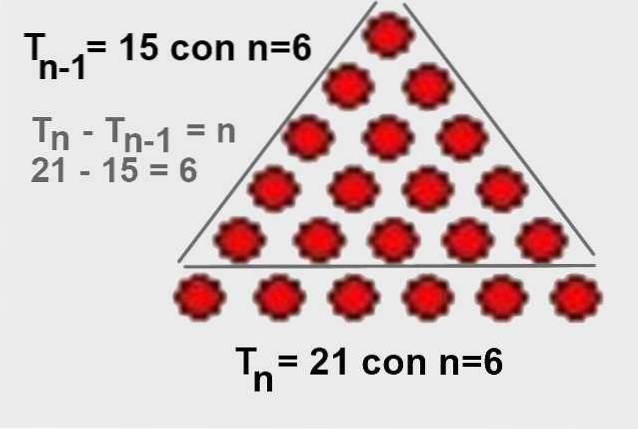
Og derfra er det tydeligt, at T_n - T_n-1 = n. Det er også let at visualisere det grafisk som vist i figur 4.

- Demo 5

Summen af ​​de første n trekantede tal Sn er lig med en sjettedel af produktet multipliceret med (n + 1) og ganget med (n + 2):

S_n = ⅙ n (n + 1) (n + 2)

Lad os bruge det trekantede antal rækkefølge n: T_n= ½ n (n + 1). Summen af ​​den første n trekantede tal betegner det med S_n  

For eksempel, S₁ betyder summen af ​​det første trekantede tal, som utvivlsomt vil være 1.

Lad os derefter se, om den formel, vi prøver at teste, er sand for n = 1:

S₁ = ⅙ 1⋅2⋅3 = 1

Faktisk er formlen for n = 1 verificeret. Det er let at visualisere, at summen af ​​de første n + 1 trekantede tal vil være summen af ​​den første n plus det næste trekantede tal:

S_{n + 1} = S_n + T_{n + 1}

Antag nu, at formlen til S_n er sandt for n, så erstatter vi det i det forrige udtryk og tilføjer det trekantede rækkefølge n + 1:

S_{n + 1} = [⅙ n (n + 1) (n + 2)] + [½ (n + 1) (n + 2)]

Lad os se trin for trin, hvad du får:

-Vi udfører summen af ​​de to fraktionerede udtryk:

S_{n + 1} = [2 n (n + 1) (n + 2) + 6 (n + 1) (n + 2)] / 12 

-Det tages fra tællerens fælles faktor til 2 (n + 1) (n + 2) og forenkler:

S_{n + 1} = 2 (n + 1) (n + 2) [n +3] / 12 = (n + 1) (n + 2) (n +3) / 6

Ovenstående resultat stemmer overens med formlen for Sn hvis n erstattes af n + 1, hvilket er blevet vist ved induktion formlen for summen af ​​de første n trekantede termer.

Tetrahedral nummer

Det således opnåede resultat kaldes tetraedrisk antal ordre n, fordi det er som at akkumulere trekantede lag, der danner en tetraeder, som vist i den følgende animation.

Referencer

1. Camacho J. Et uventet udseende af trekantede tal. Gendannet fra: masscience.com
2. Claudio. Trekantede tal. Gendannet fra: simpelthen tal. blogspot. com
3. Wikipedia. Trekantet tal. Gendannet fra: es.wikipedia.com
4. Wikipedia. Trekantet tal. Gendannet fra: en.wikipedia.com
5. Wikipedia. Tretrahedral nummer. Gendannet fra: en.wikipedia.com