Hvilke typer integraler er der?

Det typer integraler som vi finder i beregningen er de ubestemte integraler og de bestemte integraler. Selvom bestemte integraler har mange flere applikationer end ubestemte integraler, er det nødvendigt først at lære at løse ubestemte integraler..

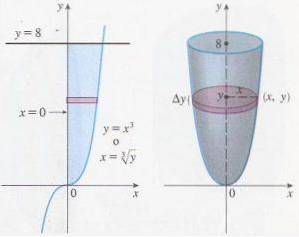
En af de mest attraktive anvendelser af bestemte integraler er beregningen af ​​volumenet af et solidt revolution. Begge typer integraler har de samme linearitetsegenskaber, og også integrationsteknikkerne afhænger ikke af typen af ​​integral.

Men på trods af at de er meget ens, er der en hovedforskel; i den første type integral er resultatet en funktion (som ikke er specifik), mens resultatet i den anden type er et tal.

Grundlæggende typer integraler

Integralverdenen er meget bred, men indeni den kan vi skelne mellem to grundlæggende typer integraler, som har stor anvendelighed i hverdagen..

1- Ubestemte integraler

Hvis F '(x) = f (x) for alle x i domænet for f, siger vi, at F (x) er en antiderivativ, en primitiv eller en integral af f (x).

Lad os på den anden side observere, at (F (x) + C) '= F' (x) = f (x), hvilket indebærer, at integriteten af ​​en funktion ikke er unik, da vi giver forskellige værdier til konstant C opnår vi forskellige antiderivativer.

Af denne grund kaldes F (x) + C det ubestemte integral af f (x) og C kaldes konstanten for integration, og vi skriver det som følger

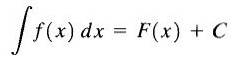
Som vi kan se, er den ubestemte integral af funktionen f (x) en familie af funktioner.

For eksempel, hvis du vil beregne den ubestemte integral af funktionen f (x) = 3x², skal du først finde et antiderivativ af f (x).

Det er let at se, at F (x) = x³ er et antiderivativ, da F '(x) = 3x². Derfor kan det konkluderes, at

∫f (x) dx = ∫3x²dx = x³ + C.

2- Bestemte integraler

Lad y = f (x) være en reel, kontinuerlig funktion på et lukket interval [a, b], og lad F (x) være et antiderivativ af f (x). Den bestemte integral af f (x) mellem grænserne a og b kaldes tallet F (b) -F (a) og betegnes som følger

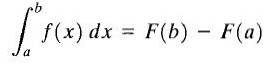
Formlen vist ovenfor er bedre kendt som "The Fundamental Theorem of Calculus." Her kaldes "a" den nedre grænse og "b" kaldes den øvre grænse. Som du kan se, er den specifikke integral af en funktion et tal.

I dette tilfælde, hvis vi beregner den bestemte integral af f (x) = 3x² i intervallet [0,3], får vi et tal.

For at bestemme dette antal vælger vi F (x) = x³ som antiderivativ for f (x) = 3x². Derefter beregner vi F (3) -F (0), som giver os resultatet 27-0 = 27. Afslutningsvis er den bestemte integral af f (x) på intervallet [0,3] 27.

Det kan bemærkes, at hvis G (x) = x³ + 3 er valgt, så er G (x) et antiderivativ af f (x), der adskiller sig fra F (x), men dette påvirker ikke resultatet, da G (3) - G (0) = (27 + 3) - (3) = 27. Af denne grund vises integrationen konstant i de bestemte integraler.

En af de mest nyttige anvendelser af denne type integral er, at det gør det muligt at beregne arealet (volumen) af et plan figur (af et solidt omdrejningstal), etablere passende funktioner og grænser for integration (og en rotationsakse).

Inden for de definerede integraler kan vi finde forskellige udvidelser af det, såsom linieintegraler, overfladeintegraler, ukorrekte integraler, flere integraler, blandt andre, alle med meget nyttige anvendelser inden for videnskab og teknik..

Referencer

1. Casteleiro, J. M. (2012). Er det let at integrere? Selvstudie manual. Madrid: ESIC.
2. Casteleiro, J. M. og Gómez-Álvarez, R. P. (2002). Integreret beregning (Illustreret red.). Madrid: ESIC Editorial.
3. Fleming, W., & Varberg, D. E. (1989). Præcalculus matematik. Prentice Hall PTR.
4. Fleming, W., & Varberg, D. E. (1989). Precalculus matematik: en problemløsningstilgang (2, Illustreret udgave). Michigan: Prentice Hall.
5. Kishan, H. (2005). Integreret beregning. Atlantic Publishers & Distributors.
6. Purcell, E. J., Varberg, D. og Rigdon, S. E. (2007). Beregning (9. udgave). Prentice hall.