
Trigonometriske forhold eksempler, øvelser og anvendelser
Det trigonometriske forhold er kvotienter eller forhold, der kan laves med værdien af siderne i en højre trekant. Disse sider er: to ben, der danner 90º med hinanden, og hypotenusen, som danner den spidse vinkel θ med et af benene.
Du kan danne 6 kvoter. Deres navne og respektive forkortelser er:
- bryst (sen)
- cosinus (cos)
- tangent (tg eller tan)
- cotangent (ctg eller cotan)
- sekant (sek) og
- cosecant (cosec)
Alle henviste til vinkel θ, som vist i følgende figur:
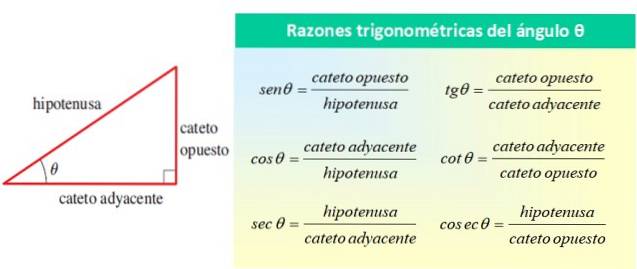
De grundlæggende trigonometriske forhold for vinklen θ er sin θ, cos θ og tan θ, mens de resterende forhold kan udtrykkes i form af disse tre. Fra ovenstående tabel kan det ses, at:
- sek θ = 1 / cos θ
- cosec θ = 1 / sin θ
- barneseng θ = 1 / tg θ
Størrelsen på siderne af trekanten påvirker ikke værdien af forholdet, da to trekanter, hvis vinkler måler det samme, er ensartede trekanter, og de respektive forhold mellem siderne har den samme værdi.
Artikelindeks
- 1 Eksempel
- 2 Løst øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Anvendelser af trigonometriske forhold
- 4 Referencer
Eksempel
Lad os f.eks. Beregne de trigonometriske forhold for vinklen θ i følgende trekanter:
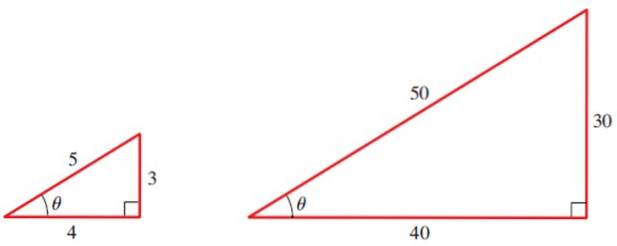
For den lille trekant har vi de tre grundlæggende forhold for vinklen θ:
sin θ = 3/5
cos θ = 4/5
tg θ = ¾
Og lad os nu beregne de tre grundlæggende forhold på θ med den store trekant:
sin θ = 30/50 = 3/5
cos θ = 40/50 = 4/5
tg θ = 30/40 = ¾
En vigtig detalje, der skal tages i betragtning, er følgende: både sin θ og cos θ er mindre end 1, da benene altid måler mindre end hypotenusen. Ja:
sin θ = 3/5 = 0,6
cos θ = 4/5 = 0,8
Løst øvelser
I de følgende øvelser bliver du bedt om at løse den rigtige trekant, hvilket betyder at finde længden af dens tre sider og målene for dens indre vinkler, hvoraf den ene altid måler 90º.
Pythagoras sætning gælder for rigtige trekanter og er meget nyttig, når to af siderne er kendt, og den manglende side skal bestemmes. Teoremet lyder således:
Hypotenusto = modsat bento + tilstødende bento
Vi kan kontrollere Pythagoras sætning med den lille trekant i figur 2, hvis ben er 3 og 4. Den rækkefølge, som benene er taget i, betyder ikke noget. Anvendelse af sætningen har vi:
Hypotenusto = 3to + 4to = 9 + 16 = 25
Derfor er hypotenusen:
Hypotenus = √25 = 5
- Øvelse 1
Beregn de trigonometriske forhold for vinklerne vist i følgende trekanter:

Løsning til
Denne trekant er den samme som i figur 3, men vi bliver bedt om de trigonometriske forhold mellem den anden skarpe vinkel, betegnet α. Påstanden tilbyder ikke hypotenusens værdi, men ved at anvende den pythagoriske sætning ved vi, at den er værd 5.
Forholdene kan beregnes direkte ud fra definitionen under forsigtighed ved valg af det ben, der er det modsatte af vinklen α at beregne sin α. Lad os se:
- sin α = 4/5
- cos α = 3/5
- tg α = 4/3
- barneseng α = ¾
- sek α = 1 / (3/5) = 5/3
- cosec α = 1 / (4/5) = 5/4
Og som vi kan se, er værdierne for de trigonometriske forhold blevet byttet. Faktisk er α og θ komplementære vinkler, hvilket betyder, at de tilføjer op til 90 °. I dette tilfælde er det rigtigt, at sin α = cos θ og så videre af de andre grunde.
Løsning b
Lad os beregne hypotenusen i trekanten ved hjælp af Pythagoras sætning:
Hypotenusto = 20to + enogtyveto = 841
√841 = 29
Derefter er de 6 trigonometriske forhold for vinklen β:
- sin β = 20/29
- cos β = 21/29
- tg β = 20/21
- barneseng β = 21/20
- sek β = 1 / (21/29) = 29/21
- cosec β = 1 / (20/29) = 20/29
- Øvelse 2
a) Find værdien af x i figuren.
b) Beregn omkredsen af de 3 viste trekanter.
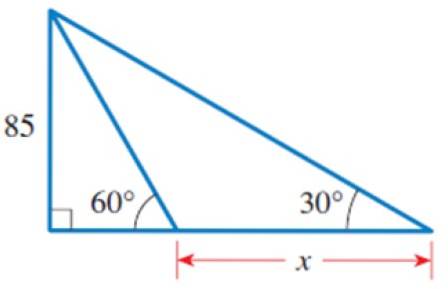
Løsning til
I figuren kan vi identificere flere trekanter, især den højre trekant til venstre, som har et ben lig med 85 og den spidse vinkel 60º.
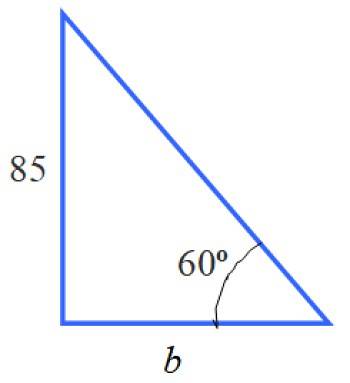
Med oplysningerne fra denne trekant kan vi beregne side b. Det er ikke den foranstaltning, der kræves i erklæringen, men at kende dens værdi er et forudgående trin.
For at bestemme dette er det passende forhold tg 60º = 85 / b, da b er benet ved siden af 60 ° og 85 er det modsatte af nævnte vinkel. Derfor:
b = 85 / tg 60º = 85 / √3
Når b er kendt, bruger vi den store og ydre højre trekant, som har en fælles side med den foregående trekant: den, der måler 85. Dette er benet overfor 30 ° vinklen..
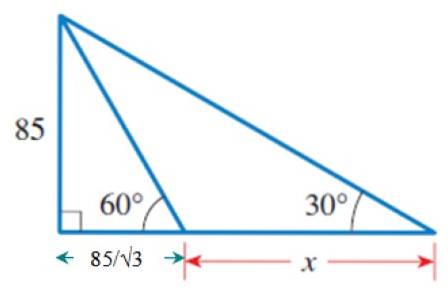
Derfra:
Ben ved siden af 30º = (85 / √3) + x
Nu kan vi foreslå følgende:
85 / [(85 / √3) + x] = tg 30º
Hvad der er i parentes multiplicerer tg 30º:
85 = [(85 / √3) + x]. tg 30º
Anvendelse af den fordelende egenskab ved multiplikation:
85 = tg 30 °. (85 / √3) + x. tg 30º
Derfor:
x.tg 30º = 85 - tg 30º. (85 / √3) = 85 [1 - tg 30º. (1 / √3)] = 85. (2/3) = 170/3
Udskiftning af værdien tg 30º = √3 / 3:
x = (170/3) ÷ (√3 / 3) = 98,15
Løsning b
Omkredsen af den lille trekant
Lad h1 hypotenusen i denne trekant, som kan beregnes ved hjælp af Pythagoras sætning eller ved hjælp af et trigonometrisk forhold, for eksempel cos 60º:
cos 60 º = 85 / √3 / h1→ h1 = (85 / √3) ÷ cos 60º = 98.1
For at finde P, omkredsen af denne trekant, tilføjer vi blot de 3 sider:
P = 85 + (85 / √3) + 98,1 = 232,2
Omkreds af den ydre trekant
Lad hto til hypotenusen i den ydre trekant:
sin 30º = 85 ÷ hto
hto = 85 ÷ sin 30º = 170
For denne trekant er omkredsen:
P = 85 + [(85 / √3) + 98,15] + 170 = 402,22
Omkreds af ikke-højre trekant
Vi kender allerede alle dens sider af denne trekant:
P = x + h1 + hto = 98,15 + 98,15 + 170 = 366,3
Anvendelser af trigonometriske forhold
Trigonometriske forhold har adskillige praktiske anvendelser, for eksempel kan højder beregnes.
Antag, at et vandtårn ligger 100 meter fra en bygning. En observatør ved et vindue bemærker, at højdevinklen for den øverste ende af tårnet er 39 º, mens den nedadgående vinkel, hvormed basens tårn ses, er 25 º. Han undrer sig:
a) Hvad er højden på tårnet?
b) Hvor højt vinduet er?
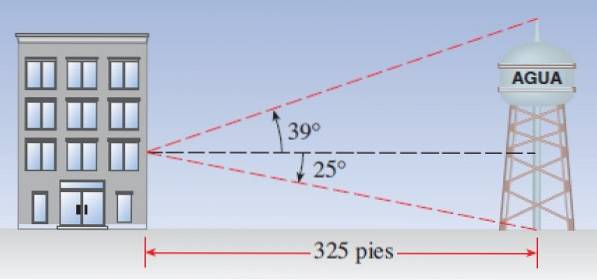
Løsning til
Fra benet overfor 39º af den øverste trekant får vi en del af svaret:
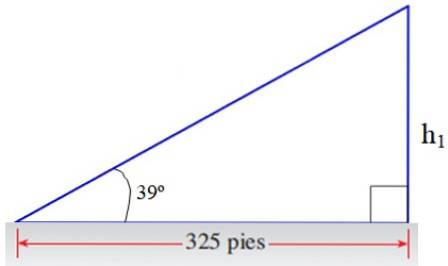
h1/ 325 = tg 39º → h1 = 325. tg 39º fod = 263,2 fod
På lignende måde opnår vi resten af tårnets højde, kaldet hto startende fra den nederste trekant:
hto/ 325 = tg 25º → hto = 325. tg 25º fod = 151.6 fod
Den samlede højde af tårnet er h1 + hto = 263,2 + 151,6 fod = 414,7 fod.
Løsning b
Vinduet er nøjagtigt i en højde hto jord:
hto = 151,6 fod.
Referencer
- Carena, M. 2019. Pre-University Mathematics Manual. National University of the Litoral.
- Hoffman, J. Selection of Mathematics Topics. Bind 3.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Matematik til beregning. 5. plads Udgave. Cengage læring.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.



Endnu ingen kommentarer