
Skrå karakteristiske linjer, ligninger og eksempler
Det skrå linjer Det er dem, der er skrå, enten med hensyn til en flad overflade eller til en anden lige, der indikerer en bestemt retning. Overvej som et eksempel de tre linjer tegnet i et plan, der vises i den følgende figur.
Vi kender deres respektive relative positioner, fordi vi sammenligner dem med en referencelinje, som normalt er X-akse betegner det vandrette.
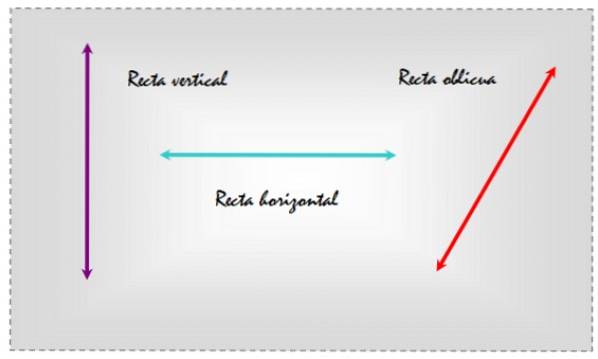
På denne måde vælges det vandrette som en reference, linjen til venstre er lodret, den i midten er vandret, og den til højre er skrå, da den er skrå i forhold til de daglige referencelinjer..
Nu optager linjerne, der er i samme plan, såsom overfladen på papiret eller skærmen, forskellige relative positioner afhængigt af om de krydser hinanden eller ej. I det første tilfælde er de sekante linjer, mens de i det andet er parallelle.
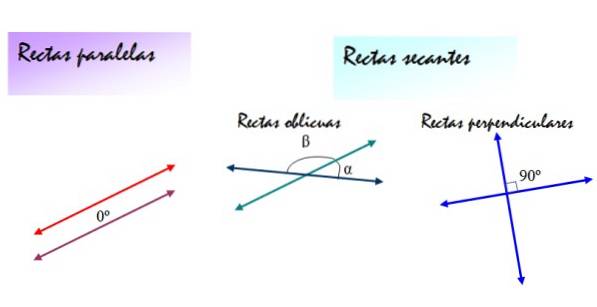
På den anden side kan de sekante linjer være skrå eller vinkelrette linjer. I begge tilfælde er skråningerne på linjerne forskellige, men de skrå linjer danner vinkler α og β imellem dem, forskellig fra 90 °, mens vinklerne bestemt af de vinkelrette linjer altid er 90 °..
Følgende figur opsummerer disse definitioner:
Artikelindeks
- 1 ligninger
- 1.1 Ligning af linjen i planet
- 2 Eksempler på skrå linjer
- 2.1 Lysstråler
- 2.2 Linjer, der ikke er i samme plan
- 3 Referencer
Ligninger
For at kende linjernes relative positioner i planet er det nødvendigt at kende den vinkel, de danner med hinanden. Bemærk, at linjerne er:
Parallel: hvis de har samme hældning (samme retning) og aldrig skærer hinanden, er deres punkter derfor lige langt fra hinanden.
Tilfældig: når alle dens punkter falder sammen og derfor har samme hældning, men afstanden mellem dens punkter er nul.
Tørring: hvis deres skråninger er forskellige, varierer afstanden mellem deres punkter, og krydset er et enkelt punkt.
Så en måde at vide, om to linjer i planet er sekant eller parallel, er gennem deres hældning. Kriterierne for parallelitet og vinkelrethed på linjerne er følgende:
Lad L være to linjer1 og Lto tilhører et plan, hvis skråninger er henholdsvis m1 og mto. Disse linjer er parallelle, hvis m1 = mto og er vinkelrette, når m1= -1 / mto
Hvis vi ikke kender hældningerne på to linjer i flyet, og at ingen af de tidligere kriterier er opfyldt, konkluderer vi, at linjerne er skrå. Ved at kende to punkter på en linje beregnes hældningen med det samme, som vi vil se i det næste afsnit.
Det er muligt at finde ud af, om to linjer er sekante eller parallelle ved at finde deres skæringspunkt og løse det ligningssystem, de danner: hvis der er en løsning, er de sekanter, hvis der ikke er nogen løsning, er de parallelle, men hvis løsningerne er uendelig, linjerne er sammenfaldende.
Dette kriterium informerer os imidlertid ikke om vinklen mellem disse linjer, selvom de krydser hinanden.
For at kende vinklen mellem linjerne er der brug for to vektorer eller Y v der hører til hver enkelt af dem. Det er således muligt at kende den vinkel, de danner ved hjælp af vektorernes skalære produkt, defineret på denne måde:
eller•v =u.v.cos α
Ligning af linjen i planet
En linje i det kartesiske plan kan repræsenteres på flere måder, såsom:
-Hældningsafskæringsform: Ja m er hældningen på linjen og b er krydset mellem linjen og den lodrette akse, ligningens linie er y = mx + b.
-Generel ligning for en lige linje: Ax + By + C = 0, hvor m = A / B er skråningen.
I det kartesiske plan er de lodrette og vandrette linjer særlige tilfælde af linjens ligning.
-Lodrette linjer: x = a
-Vandrette linjer: y = k
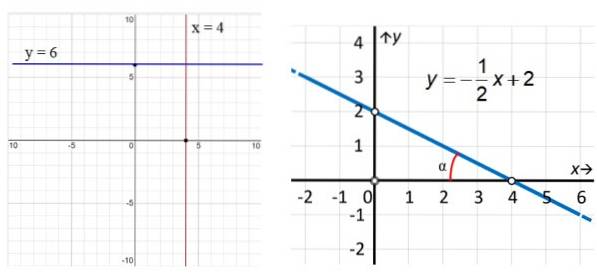
I eksemplerne i figur 3 har den lodrette røde linje ligning x = 4, mens linjen parallel med x-aksen (blå) har ligning y = 6. Hvad angår linjen til højre ser vi, at den er skrå og til find dens ligning, vi bruger de punkter, der er fremhævet i figuren: (0,2) og (4,0) på denne måde:
m = (ogto - Y1) / (xto - x1) = (2 - 0) / (0 - 4) = - ½
Skæringen af denne linje med den lodrette akse er y = 2, som det fremgår af grafen. Med denne information:
y = (-½) x + 2
Det er let at bestemme hældningsvinklen i forhold til x-aksen. Jeg føler at:
α = arctg (2/4) = 26,6º
Derfor er den positive vinkel fra x-aksen til linjen: 180º - 26,6º = 153,4º
Eksempler på skrå linjer

Skrå linjer vises mange steder, det er et spørgsmål om at være opmærksom på at finde dem inden for arkitektur, sport, ledninger til strømforsyning, rør og mange flere steder. I naturen er der også skrå linjer, som vi vil se nedenfor:
Lysstråler
Sollys bevæger sig i en lige linje, men Jordens afrundede form påvirker, hvordan sollys rammer overfladen..
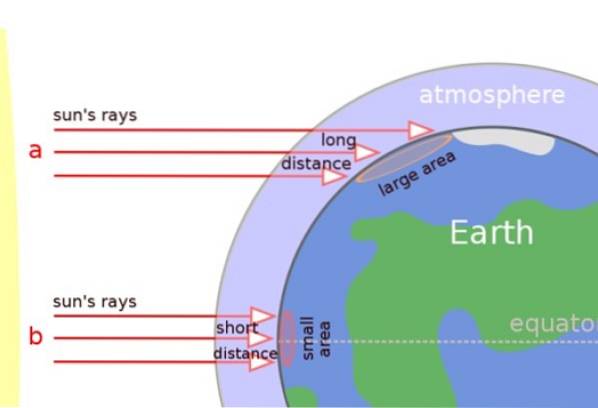
På billedet nedenfor kan vi tydeligt se, at solens stråler strejker vinkelret i tropiske områder, men i stedet skråt når overfladen i tempererede områder og ved polerne..
Dette er grunden til, at solens stråler kører en længere afstand gennem atmosfæren, og varmen spredes også over en større overflade (se figur). Resultatet er, at områderne nær polerne er koldere.
Linjer, der ikke er i samme plan
Når to linjer ikke er i samme plan, kan de stadig være skrå eller skævt, som de også er kendt. I dette tilfælde er deres direktørvektorer ikke parallelle, men da de ikke tilhører det samme plan, skærer disse linjer ikke hinanden.
For eksempel er linjerne i figur 6 til højre tydeligt på forskellige plan. Hvis du ser på dem ovenfra, kan du se, at de faktisk skærer hinanden, men de har ikke et fælles punkt. Til højre ser vi hjulene på cyklen, hvis eger ser ud til at krydse, set forfra.

Referencer
- Geometri. Direktør vektor af en linje. Gendannet fra: juanbragado.es.
- Larson, R. 2006. Calculus med analytisk geometri. 8. plads Udgave. Mcgraw bakke.
- Matematik er et spil. Linjer og vinkler. Gendannet fra: juntadeandalucia.es.
- Lige linjer, der krydser hinanden. Gendannet fra: profesoraltuna.com.
- Villena, M. Analytisk geometri i R3. Gendannet fra: dspace.espol.edu.ec.



Endnu ingen kommentarer