Højre hånd regel første og anden regel, applikationer, øvelser

Det højre hånd regel er en hukommelsesressource til at bestemme retningen og følelsen af ​​vektoren, der stammer fra et vektorprodukt eller krydsprodukt. Det bruges i vid udstrækning i fysik, da der er vigtige vektormængder, der er resultatet af et vektorprodukt. Sådan er for eksempel drejningsmoment, magnetisk kraft, vinkelmoment og magnetisk moment.

Lad være to generiske vektorer til Y b hvis krydsprodukt er til x b. Modulet til en sådan vektor er:

til x b = a.b. i α

Hvor α er den mindste vinkel mellem til Y b, mens a og b repræsenterer dets moduler. For at skelne vektorerne i deres moduler bruges der fed skrift.

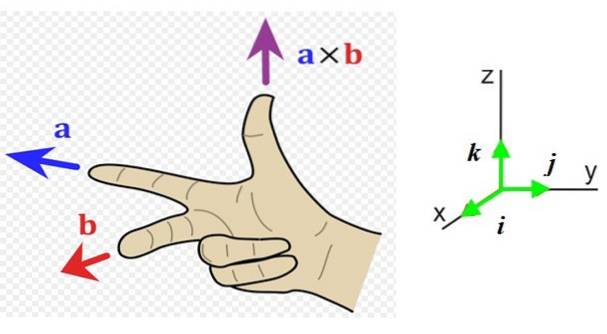
Nu skal vi kende retningen og følelsen af ​​denne vektor, så det er praktisk at have et referencesystem med de tre retninger af rummet (figur 1 til højre). Enhedsvektorerne jeg, j Y k de peger henholdsvis mod læseren (fra siden), til højre og op.

I eksemplet i figur 1 til venstre, vektoren til hoveder mod venstre (retning Y negativ og pegefinger på højre hånd) og vektoren b går til læseren (retning x positiv, langfinger på højre hånd).

Den resulterende vektor til x b har tommelfingerretningen opad i retningen z positiv.

Artikelindeks

• 1 Anden regel for højre hånd
  • 1.1 Alternativ regel for højre hånd
• 2 applikationer
  • 2.1 Vinkelhastighed og acceleration
  • 2.2 Vinkelmomentet
• 3 Øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referencer

Anden regel for højre hånd

Denne regel, også kaldet højre tommelfingerregel, Det bruges meget, når der er størrelser, hvis retning og retning roterer, såsom magnetfeltet B produceret af en tynd, lige ledning, der bærer en strøm.

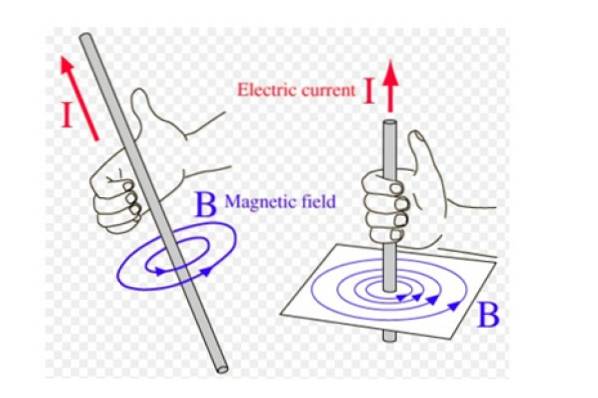
I dette tilfælde er magnetfeltlinjerne koncentriske cirkler med ledningen, og rotationsretningen opnås med denne regel på følgende måde: højre tommelfinger peger i strømens retning og de resterende fire fingre er buet i retning af landskabet. Vi illustrerer konceptet i figur 2.

Alternativ højre håndregel

Figuren nedenfor viser en alternativ form for højrehåndsreglen. Vektorerne, der vises i illustrationen, er:

-Fart v af en punktafgift q.

-Magnetfelt B inden for hvilken lasten bevæger sig.

-F_B den kraft, som magnetfeltet udøver på ladningen.

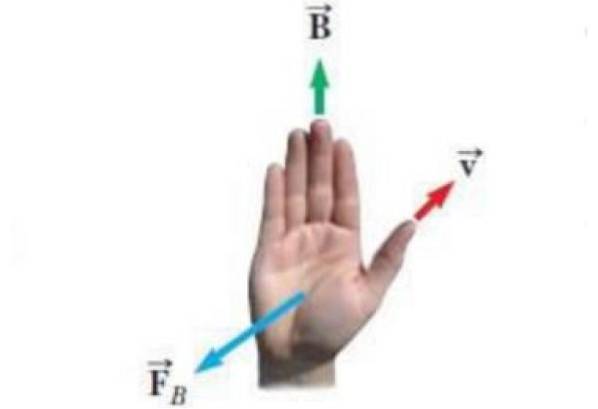
Ligningen for den magnetiske kraft er F_B = qv x B og reglen om højre hånd til at kende retningen og følelsen af F_B anvendes således: tommelfingeren peger i henhold til v, de fire resterende fingre placeres i henhold til felt B. Derefter F_B er en vektor, der kommer ud af håndfladen, vinkelret på den, som om den skubber belastningen.

Noter det F_B Jeg vil pege i den modsatte retning hvis opladningen q var negativ, da vektorproduktet ikke er kommutativt. Faktisk:

til x b = - b x til

Ansøgninger

Højrehåndsreglen kan anvendes til forskellige fysiske størrelser, lad os kende nogle af dem:

Vinkelhastighed og acceleration

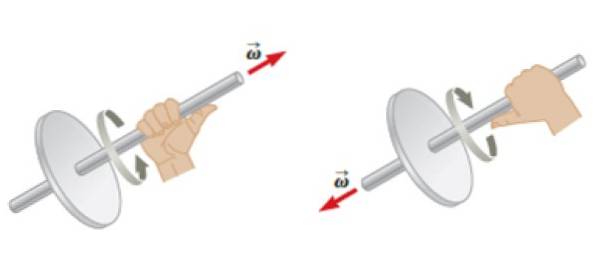
Begge vinkelhastigheder ω som vinkelacceleration a de er vektorer. Hvis et objekt roterer omkring en fast akse, er det muligt at tildele retningen og følelsen af ​​disse vektorer ved hjælp af højre håndregel: de fire fingre krølles efter rotation og tommelfingeren giver straks retningen og følelsen af ​​vinkelhastighed ω.

For sin del vinkelacceleration a vil have samme adresse som ω, men dens betydning afhænger af, om ω øges eller falder i størrelse over tid. I det første tilfælde har begge samme retning og forstand, men i det andet vil de have modsatte retninger..

Vinkelmoment

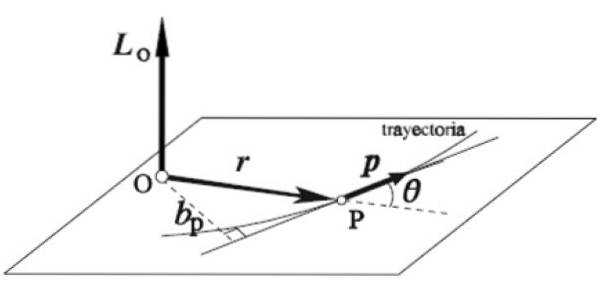
Vinkelmomentvektoren L_ELLER af en partikel, der roterer omkring en bestemt akse O, er defineret som vektorproduktet fra dets øjeblikkelige positionsvektor r  og det lineære momentum s:

L = r x s

Højrehåndsreglen anvendes på denne måde: pegefingeren placeres i samme retning og følelse af r, langfingeren på den af s, begge på et vandret plan, som på figuren. Tommelfingeren strækkes automatisk lodret opad, hvilket indikerer retningen og følelsen af ​​vinkelmoment L_ELLER.

Uddannelse

- Øvelse 1

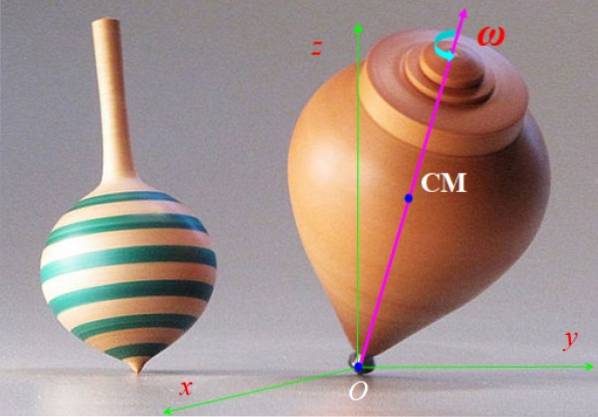
Toppen i figur 6 drejer hurtigt med vinkelhastighed ω og symmetriaksen roterer langsommere omkring den lodrette akse z. Denne bevægelse kaldes presession. Beskriv de kræfter, der virker på snurretoppen og den effekt, de producerer.

Opløsning

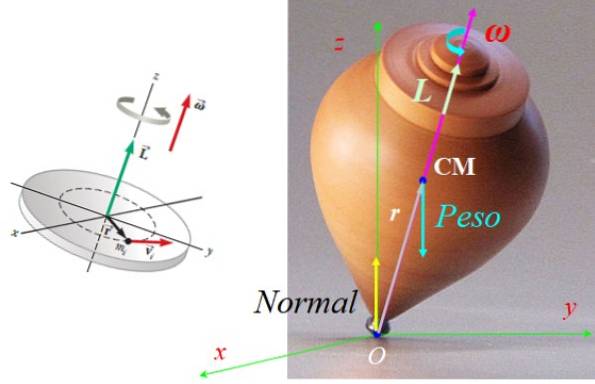
De kræfter, der virker på toppen, er normale N, påført på omdrejningspunktet med jorden O plus vægten Mg, anvendt i centrum af masse CM med g tyngdekraftens accelerationsvektor, lodret lodret nedad (se figur 7).

Begge kræfter balancerer, derfor bevæger toppen sig ikke. Vægten producerer dog et drejningsmoment eller drejningsmoment τ netto med hensyn til punkt O, givet af:

τ_ELLER = r_ELLER x F, med F = Mg.

Hvad r og Mg de er altid i samme plan som toppen roterer, i henhold til højre hånd drejningsmomentet τ_ELLER er altid placeret på flyet xy, vinkelret på begge dele r Hvad g.

Noter det N producerer ikke et drejningsmoment i forhold til O, fordi dens vektor r med hensyn til O er nul. Dette drejningsmoment frembringer en ændring i vinkelmomentet, der får toppen til at gå foran Z-aksen..

- Øvelse 2

Angiv retningen og følelsen af ​​den vinkelmomentvektor L på toppen af ​​figur 6.

Opløsning

Ethvert punkt på toppen har masse m_jeg, hastighed v_jeg og placeringsvektor r_jeg, når den roterer omkring z-aksen. Vinkelmoment L_jeg af nævnte partikel er:

L_jeg = r_jeg x s_jeg = r_jeg x m_jegv_jeg

På grund af r_jeg Y v_jeg er vinkelrette, størrelsen af L det er:

L_jeg = m_jegr_jegv_jeg

Lineær hastighed v er relateret til vinkelhastigheden ω igennem:

v_jeg = r_jegω

Derfor:

L_jeg = m_jegr_jeg (r_jegω) = m_jegr_jeg^toω

Den samlede vinkelmoment for roterende top L er summen af ​​vinkelmomentet for hver partikel:

L = (∑m_jegr_jeg^to ) ω

∑ m_jegr_jeg^to  er inerti-øjeblikket I fra toppen, så:

L= Jegω

Derfor L Y ω har samme retning og forstand som vist i figur 7.

Referencer

1. Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill. 
2. Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 
3. Kirkpatrick, L. 2007. Fysik: Et blik på verden. 6. forkortede udgave. Cengage læring.
4. Knight, R. 2017. Fysik for forskere og teknik: en strategi tilgang. Pearson. 
5. Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1 og 2. 7. Ed. Cengage Learning.