
Green's sætning, bevis, applikationer og øvelser
Det Green's sætning er en beregningsmetode, der bruges til at relatere linjeintegraler med dobbeltareal eller overfladeintegraler. De involverede funktioner skal betegnes som vektorfelter og defineres inden for stien C.
For eksempel kan et linjeintegralt udtryk være meget vanskeligt at løse; dog ved at implementere Greens sætning bliver dobbelt integraler ret grundlæggende. Det er altid vigtigt at respektere den positive retning af banen, dette refererer til retning mod uret.

Greens sætning er et særligt tilfælde af Stokes sætning, hvor projiceringen af vektorfunktionen udføres i xy-planet.
Artikelindeks
- 1 Definition
- 2 demo
- 3 applikationer
- 4 Historie
- 5 Forhold til andre sætninger
- 6 Øvelser
- 7 Referencer
Definition
Udtrykket af Greens sætning er som følger:
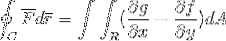
Det første udtryk viser linjen integreret defineret af stien "C" for det skalære produkt mellem vektorfunktionen "F" og den for vektoren "r".
C: Det er den definerede sti, hvor vektorfunktionen projiceres, så længe den er defineret for det plan.
F: Vektorfunktion, hvor hver af dens komponenter er defineret af en funktion som sådan (f, g).
r: Det er en vektor, der tangerer regionen R, over hvilken integralet er defineret. I dette tilfælde fungerer vi med en differens af denne vektor.
I det andet udtryk ser vi Green's sætning udviklet, hvor den dobbelte integral defineret i regionen R af forskellen mellem de partielle derivater af g og f, med hensyn til henholdsvis x og y, observeres. Ved en områdedifferentiale, der ikke er mere end produktet af begge to-dimensionelle differentier (dx.dy).
Denne sætning er perfekt anvendelig til rum- og overfladeintegraler.
Demonstration
For at bevise Greens sætning på en enkel måde opdeles denne opgave i 2 dele. Først antager vi, at vektorfunktionen F kun har definition i versoren jeg. Mens funktionen "g" svarer til versoren j vil være lig med nul.
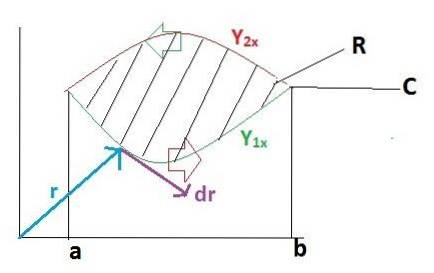
F = f (x, y)jeg + g (x, y)j = f (x, y)jeg + 0
r = xjeg + Yj
dr = dxjeg + D yj
Først udvikler vi linjen integreret over banen C, for hvilken banen er blevet opdelt i 2 sektioner, der går først fra a til b og derefter fra b til a.
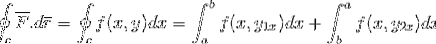
Definitionen af den grundlæggende sætning af calculus anvendes til en bestemt integral.
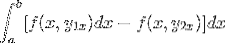
Udtrykket omorganiseres til en enkelt integral, det negative gøres til en fælles faktor, og rækkefølgen af faktorerne vendes.
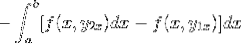
Når vi observerer dette udtryk i detaljer, bliver det tydeligt, at når vi anvender de primitive funktionskriterier, er vi i nærværelse af integralet af udtrykket afledt af f med hensyn til y. Evalueret i parametre
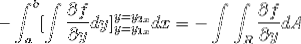
Nu er det nok at antage, at vektorfunktionen F kun er defineret for g (x, y)j. Når man opererer på en måde svarende til det foregående tilfælde, opnås følgende:
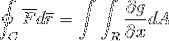
For at afslutte tages de 2 bevis og sammenføjes i det tilfælde, hvor vektorfunktionen tager værdier for begge versores. På denne måde vises det, hvordan linjen integreret efter at være defineret og betragtes som en endimensionel bane, kan udvikles fuldt ud til planet og rummet.
F = f (x, y)jeg + g (x, y)j
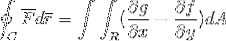
På denne måde bevises Greens sætning.
Ansøgninger
Anvendelsen af Greens sætning er bred inden for grene af fysik og matematik. Disse strækker sig til enhver applikation eller anvendelse, der kan gives til linjeintegration.
Det mekaniske arbejde udført af en kraft F gennem en sti C kan udvikles af en linieintegral, der udtrykkes som en dobbeltintegral af et område ved hjælp af Green's sætning.
Inertimomenterne for mange kroppe, der udsættes for eksterne kræfter på forskellige anvendelsessteder, reagerer også på linieintegraler, der kan udvikles med Greens sætning..
Dette har flere funktioner i resistensundersøgelser af materialer, der er i brug. Hvor eksterne værdier kan kvantificeres og tages i betragtning inden udarbejdelsen af forskellige elementer.
Generelt letter Green's sætning forståelsen og definitionen af de områder, hvor vektorfunktioner er defineret med hensyn til en region i henhold til en bane.
Historie
Det blev offentliggjort i 1828 i værket Matematisk analyse af teorierne om elektricitet og magnetisme, skrevet af den britiske matematiker George Green. I det udforskes ganske afgørende afsnit i anvendelsen af calculus i fysik, såsom begrebet potentielle funktioner, Green's funktioner og anvendelserne af hans selvtitulerede sætning.
George Green formaliserede sin studiekarriere i en alder af 40 år og var indtil nu en helt selvlært matematiker. Efter at have studeret ved University of Cambridge, fortsatte han sin forskning med bidrag til akustik, optik og hydrodynamik, der stadig er gyldige i dag..
Forholdet til andre sætninger
Greens sætning er et specielt tilfælde, og det stammer fra 2 andre meget vigtige sætninger inden for beregningsområdet. Disse er Kelvin-Stokes sætning og divergens sætning eller Gauss Ostrogradski.
Fra en af de to sætninger er det muligt at nå frem til Greens sætning. Visse definitioner og forslag er nødvendige for at udvikle sådanne beviser..
Uddannelse
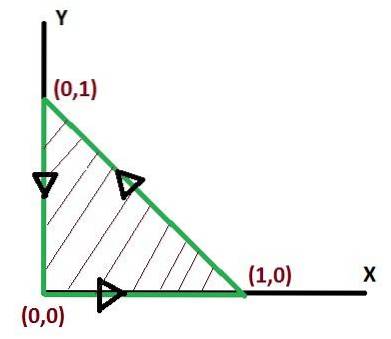
- Følgende øvelse viser, hvordan man transformerer en linjeintegral til en dobbeltintegral i forhold til en region R.
Det originale udtryk er følgende:
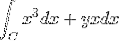
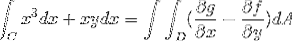
Fra hvor funktionerne svarende til f og g er taget
f (x, y) = x3 g (x, y) = yx
df / dy = 0 dg / dx = y
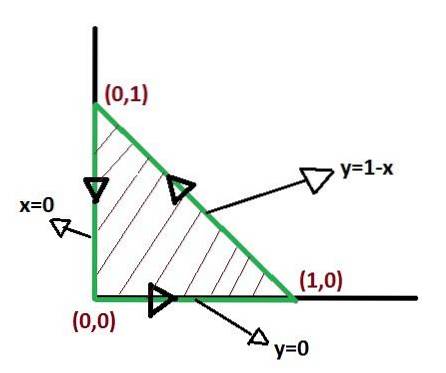
Der er ingen enkelt måde at definere grænserne for integration ved anvendelse af Green's sætning. Men der er måder, hvor integralerne efter at være defineret kan være enklere. Optimering af integrationsgrænserne fortjener opmærksomhed.
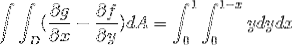
Hvor vi løser integralerne, får vi:
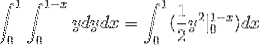
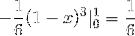
Denne værdi svarer i kubiske enheder til området under vektorfunktionen og over det trekantede område defineret af C.
I tilfælde af linieintegral uden at udføre Green's metode ville det have været nødvendigt at parametrere funktionerne i hver sektion i regionen. Det vil sige udføre 3 parametriserede integraler til opløsningen. Dette er tilstrækkeligt bevis for den effektivitet, som Robert Green bragte med sin sætning til beregning.
Referencer
- Introduktion til kontinuummekanik. W Michael Lai, David H. Rubin, Erhard Krempl, David Rubin Butterworth-Heinemann, 23. juli. 2009
- Multivariabel beregning. James Stewart. Cengage Learning, 22. mar 2011
- En uformel historie om Green's sætning og tilknyttede ideer. James Joseph Cross. Institut for Matematik, University of Melbourne, 1975
- Varmeledning ved hjælp af grønne funktioner. Kevin D. Cole, James V. Beck, A. Haji-Sheikh, Bahman Litkouhi. Taylor & Francis, 16. jul 2010
- Anvendelse af Green's sætning til ekstremisering af lineære integraler. Forsvars tekniske informationscenter, 1961



Endnu ingen kommentarer