Torricellis sætning hvad den består af, formler og øvelser

Det Torricellis sætning Torricelli-princippet fastslår, at hastigheden af ​​væsken, der kommer ud gennem hullet i væggen i en tank eller beholder, er identisk med hastigheden på en genstand, der får lov til at falde frit fra en højde svarende til væskens frie overflade op til hullet.

Teoremet er illustreret i følgende figur:

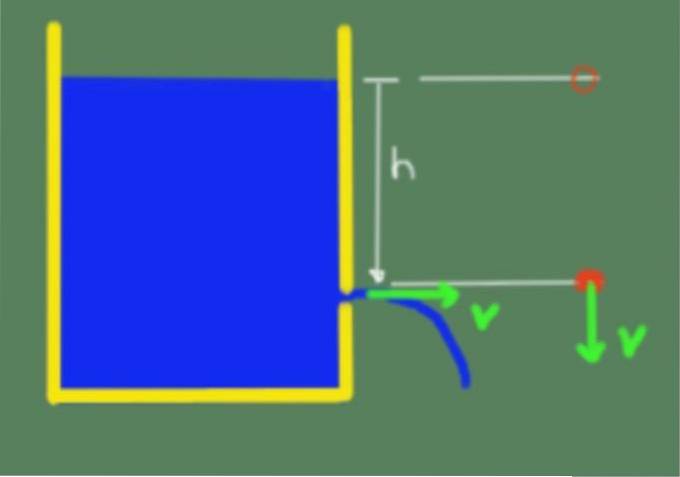
På grund af Torricellis sætning kan vi derefter bekræfte, at væskens udgangshastighed gennem en åbning, der er i højden h under væskens frie overflade, er givet ved følgende formel:

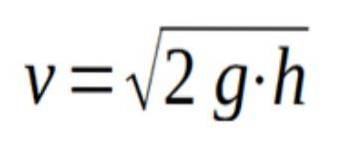
Hvor g er tyngdeacceleration, og h er højden fra hullet til væskens frie overflade.

Evangelista Torricelli var en fysiker og matematiker født i byen Faenza, Italien i 1608. Torricelli er anerkendt for opfindelsen af ​​kviksølvbarometeret og i anerkendelse er der en trykenhed kaldet “torr” svarende til en millimeter kviksølv (mm Hg).

Artikelindeks

• 1 Bevis for sætningen
  • 1.1 Faldende genstand
  • 1.2 Væske kommer ud af hullet
• 2 Løst øvelser
  • 2.1 Øvelse 1
• 3 I) Det lille udløbsrør til en vandtank er 3 m under vandoverfladen. Beregn vandets udgangshastighed.
  • 3.1 Øvelse 2
  • 3.2 Øvelse 3
• 4 Referencer

Bevis for sætningen

I Torricellis sætning og i formlen, der giver hastigheden, antages det, at viskositetstabene er ubetydelige, ligesom i frit fald antages det, at friktionen på grund af luften omkring det faldende objekt er ubetydelig..

Ovenstående antagelse er i de fleste tilfælde rimelig og involverer også bevarelse af mekanisk energi.

For at bevise sætningen finder vi først formlen for hastigheden for et objekt, der frigøres uden starthastighed nul, fra samme højde som væskeoverfladen i tanken..

Princippet om energibesparelse vil blive anvendt for at opnå den faldende genstands hastighed lige når den er faldet ned i en højde h lig med det fra hul til fri overflade.

Da der ikke er friktionstab, er det gyldigt at anvende princippet om bevarelse af mekanisk energi. Antag at den faldende genstand har masse m, og at højden h måles fra væskens udgangsniveau.

Faldende genstand

Når genstanden frigøres fra en højde svarende til væskens frie overflade, er dens energi kun tyngdepotentiale, da dens hastighed er nul og derfor er dens kinetiske energi nul. Den potentielle energi Ep er givet af:

Ep = m g h

Når den passerer foran hullet, er dens højde nul, så er den potentielle energi nul, så den har kun kinetisk energi Ec givet af:

Ec = ½ m v^to

Da energien er konserveret, er Ep = Ec fra det, der opnås:

½ m v^to = m g h

Løser for hastighed v Torricelli-formlen opnås derefter:

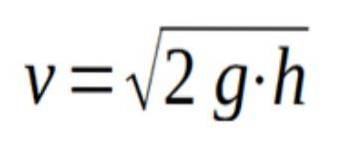
Væske kommer ud af hullet

Dernæst finder vi væskens udgangshastighed gennem hullet for at vise, at den falder sammen med det, der netop blev beregnet for et frit faldende objekt.

Til dette vil vi basere os på Bernoullis princip, som ikke er andet end bevarelse af energi, der påføres væsker.

Bernoullis princip er formuleret således:

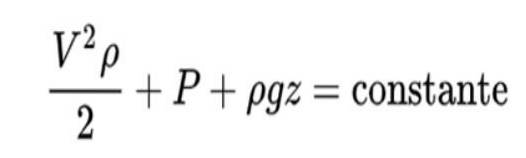
Fortolkningen af ​​denne formel er som følger:

• Det første udtryk repræsenterer væskens kinetiske energi pr. Volumenhedsenhed
• Det andet repræsenterer arbejdet udført ved tryk pr. Tværsnitsareaenhed.
• Den tredje repræsenterer tyngdekraftens potentielle energi pr. Volumenvolumen..

Da vi går ud fra den forudsætning, at det er en ideel væske under ikke-turbulente forhold med relativt lave hastigheder, er det relevant at bekræfte, at den mekaniske energi pr. Volumen enhed i væsken er konstant i alle regioner eller tværsnit af samme..

I denne formel V er væskens hastighed, ρ væskens tæthed, P tryk og z lodret position.

Figuren nedenfor viser Torricelli-formlen startende fra Bernoullis princip.

Vi anvender Bernoullis formel på den frie overflade af væsken betegnet med (1) og på udgangshullet betegnet med (2). Nulhovedniveauet er valgt flugter med udløbshullet.

Under forudsætningen om, at tværsnittet i (1) er meget større end i (2), kan vi derefter antage, at hastigheden for nedstigning af væsken i (1) er praktisk talt ubetydelig.

Dette er grunden til V₁= 0, det tryk, som væsken udsættes for i (1), er atmosfærisk tryk, og højden målt fra åbningen er h.

For udløbssektionen (2) antager vi, at udløbshastigheden er v, det tryk, som væsken udsættes for ved udløbet, er også atmosfærisk tryk, og udløbshøjden er nul.

Værdierne svarende til sektionerne (1) og (2) erstattes i Bernoullis formel og indstilles ens. Ligestillingen gælder, fordi vi antager, at væsken er ideel, og at der ikke er noget tyktflydende friktionstab. Når alle vilkårene er forenklet, opnås hastigheden ved udgangshullet.

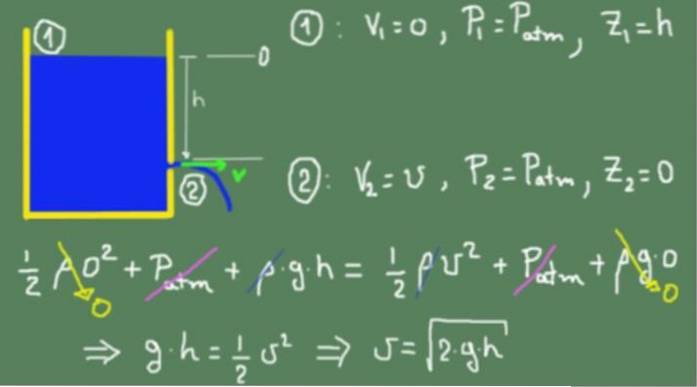
Rammen ovenfor viser, at det opnåede resultat er det samme som for et frit faldende objekt,

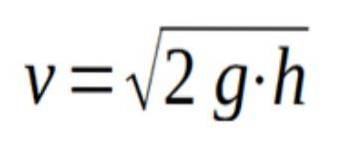
Løst øvelser

Øvelse 1

jeg) Det lille udløbsrør til en vandtank er 3 m under vandoverfladen. Beregn vandets udgangshastighed.

Opløsning:

Den følgende figur viser, hvordan Torricellis formel anvendes i denne sag.

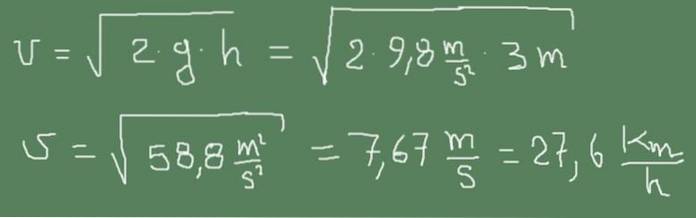
Øvelse 2

IIForudsat at tankens udløbsrør fra forrige øvelse har en diameter på 1 cm, beregnes vandudløbsstrømmen.

Opløsning:

Strømningshastigheden er væskens volumen, der udgår pr. Tidsenhed, og beregnes simpelthen ved at gange området for udgangsåbningen med udgangshastigheden.

Følgende figur viser detaljerne i beregningen.

Øvelse 3

III) Bestem, hvor høj den frie overflade af vandet er i en beholder, hvis du kender det

at vandet i et hul i bunden af ​​beholderen kommer ud ved 10 m / s.

Opløsning:

Selv når hullet er i bunden af ​​beholderen, kan Torricelli-formlen stadig anvendes.

Følgende figur viser detaljerne i beregningerne.

Referencer

1. Wikipedia. Torricellis sætning.
2. Hewitt, P.. Konceptuel fysik. Femte udgave.119.
3. Unge, Hugh. 2016. Sears-Zemanskys universitetsfysik med moderne fysik. 14. udgave. Pearson. 384.