
Grundlæggende sætning af aritmetisk bevis, anvendelser, øvelser

Det Den grundlæggende sætning af aritmetik angiver, at ethvert naturligt tal større end 1 kan nedbrydes som et produkt af primtal - nogle kan gentages - og denne form er unik for dette tal, selv om rækkefølgen af faktorer kan være forskellig.
Husk at et primtal s Det er den, der kun indrømmer sig selv og 1 som positive delere. Følgende tal er primære: 2, 3, 5, 7, 11, 13 og så videre, da der er uendelige. Nummer 1 betragtes ikke som en primær, fordi det har en enkelt skiller.

For deres del kaldes de numre, der ikke overholder ovenstående sammensatte tal, som 4, 6, 8, 9, 10, 12, 14 ... Lad os tage tallet 10 for eksempel, og straks ser vi, at det kan nedbrydes som et produkt af 2 og 5:
10 = 2 × 5
Både 2 og 5 er faktisk primtal. Teoremet siger, at dette er muligt for ethvert tal n:
Hvor s1, sto, s3... sr er primtal og k1, kto, k3,... kr de er naturlige tal. Så primtalene fungerer som murstenene, hvorfra de naturlige tal bygges gennem multiplikation.
Artikelindeks
- 1 Bevis på den grundlæggende sætning af aritmetik
- 1.1 Enhed ved primærfaktorisering
- 2 applikationer
- 2.1 Primtal i naturen
- 2.2 Primtal og online shopping
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Bevis for den grundlæggende sætning af aritmetik
Vi begynder med at vise, at hvert tal kan nedbrydes til primære faktorer. Lad være et naturligt tal n> 1, prime eller komposit.
For eksempel, hvis n = 2, kan det udtrykkes som: 2 = 1 × 2, hvilket er prime. På samme måde skal du fortsætte med følgende tal:
3 = 1 × 3
4 = 2 × 2
5 = 1 × 5
6 = 2 × 3
7 = 1 × 7
8 = 2 × 2 × 2
Vi fortsætter sådan og nedbryder alle de naturlige tal, indtil vi når tallet n -1. Lad os se, om vi kan gøre det med følgende nummer: n.
Hvis n er primær, kan vi nedbryde det som n = 1 × n, men antag at n er sammensat og har en divisor d, logisk mindre end n:
1< d < n.
Hvis n / d = p1, med P1 et primtal, så skrives n som:
n = p1.d
Hvis d er prime, er der ikke mere at gøre, men hvis det ikke er, er der et tal nto som er en skillerum af d og mindre end dette: nto < d, por lo que d podrá escribirse como el producto de nto med et andet primtal sto:
d = sto nto
At når man udskifter i det originale nummer n, ville det give:
n = p1 .sto .nto
Antag nu, at nto enten er et primtal, og vi skriver det som et primtaltal p3, af en divisor af dig n3, sådan at n3 < nto < n1 < n:
nto = s3.n3 → n = s1 sto s3.n3
Vi gentager denne procedure et begrænset antal gange, indtil vi opnår:
n = p1.sto.s3 ... sr
Det betyder, at det er muligt at nedbryde alle sammen heltal fra 2 til n, som et produkt af primtal.
Unikt ved primærfaktorisering
Lad os nu kontrollere, at bortset fra faktorernes rækkefølge er denne nedbrydning unik. Antag at n kan skrives på to måder:
n = p1.sto.s3 ... sr = q1.hvadto.hvad3... hvads (med r ≤ s)
Selvfølgelig det1, hvadto, hvad3... er også primtal. Som s1 del a (q1.hvadto.hvad3... hvads) Så s1 er lig med noget af "q", betyder det ikke noget til hvilket, så vi kan sige, at s1 = q1. Vi deler n med s1 og vi får:
sto.s3 ... sr =.hvadto.hvad3... hvads
Vi gentager proceduren, indtil vi deler alt med sr, så får vi:
1 = qr + 1... hvads
Men det er ikke muligt at komme til hvadr + 1... hvads = 1 når r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.
Ansøgninger
Som vi har sagt før, repræsenterer primtalene, hvis du vil, atomernes tal, deres grundlæggende komponenter. Så den grundlæggende sætning i aritmetik har adskillige anvendelser, den mest oplagte: vi kan arbejde lettere med store tal, hvis vi udtrykker dem som et produkt af mindre antal..
På samme måde kan vi finde det største fælles multiplum (LCM) og den største fælles divisor (GCF), en procedure, der hjælper os med at lave summer af fraktioner lettere, finde rødder af et stort antal eller operere med radikaler, rationalisere og løse applikationsproblemer af meget forskelligartet karakter.
Desuden er primtalene ekstremt gådefulde. Et mønster genkendes endnu ikke i dem, og det er ikke muligt at vide, hvilken der bliver næste. Den største hidtil blev fundet af computere og har 24.862.048 cifre, skønt de nye primtal vises sjældnere hver gang.
Primtal i naturen
Cicadas, cicádidos eller cicadas, der lever i den nordøstlige del af USA, opstår i cykler på 13 eller 17 år. De er begge primtal.
På denne måde undgår cikaderne at falde sammen med rovdyr eller konkurrenter, der har andre fødselsperioder, og heller ikke de forskellige sorter af cikader konkurrerer med hinanden, da de ikke falder sammen i det samme år..

Primtal og online shopping
Primtal bruges i kryptografi for at holde kreditkortoplysninger hemmelige, når de foretager køb over internettet. På denne måde kommer de data, som køberen ankommer nøjagtigt til butikken uden at gå tabt eller falde i hænderne på skruppelløse mennesker..
Hvordan? Dataene på kortene er kodet i et tal N, der kan udtrykkes som produktet af primtal. Disse primtal er nøglen, som dataene afslører, men de er ukendte for offentligheden, de kan kun afkodes på nettet, som de er rettet mod.
Nedbrydning af et tal i faktorer er en let opgave, hvis tallene er små (se de løste øvelser), men i dette tilfælde bruges primtal på 100 cifre som en nøgle, som når man multiplicerer dem giver meget større tal, hvis detaljerede nedbrydning indebærer en kæmpe opgave.
Løst øvelser
- Øvelse 1
Nedbryd 1029 til primære faktorer.
Opløsning
1029 kan deles med 3. Det vides, fordi summen er et multiplum af 3: 1 + 0 + 2 + 9 = 12, når man tilføjer sine cifre. Da faktorernes rækkefølge ikke ændrer produktet, kan vi starte der:
1029 3
343
1029 = 3 × 343
På den anden side 343 = 73, derefter:
1029 = 3 × 73 = 3 × 7 × 7 × 7
Og da både 3 og 7 er primtal, er dette nedbrydningen af 1029.
- Øvelse 2
Faktor trinomialet xto + 42x + 432.
Opløsning
Trinomialet omskrives i form (x + a). (x + b), og vi skal finde værdierne for a og b, således at:
a + b = 42; a.b = 432
Nummeret 432 nedbrydes til primære faktorer, og derfra vælges den passende kombination ved prøve og fejl, så de tilføjede faktorer giver 42.
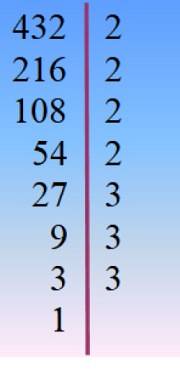
432 = 24 × 33 = 2 × 33× 23 = 24× 3to × 3 =…
Herfra er der flere muligheder for at skrive 432:
432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72 ... .
Og alle kan findes ved at kombinere produkter mellem de vigtigste faktorer, men for at løse den foreslåede øvelse er den eneste passende kombination: 432 = 24 × 18 siden 24 + 18 = 42, så:
xto + 42x + 432 = (x + 24). (x +18)
Referencer
- Baldor, A. 1986. Teoretisk praktisk aritmetik. Compañía Cultural Editora de Textos Americanos S.A.
- BBC World. Den skjulte naturkode. Gendannet fra: bbc.com.
- De Leon, Manuel Primtal: Internets vogtere. Gendannet fra: blogs.20minutos.es.
- UNAM. Number Theory I: Fundamental Theorem of Arithmetic. Gendannet fra: teoriadenumeros.wikidot.com.
- Wikipedia. Den grundlæggende sætning af aritmetik. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer