
Tredje lov om termodynamik formler, ligninger, eksempler
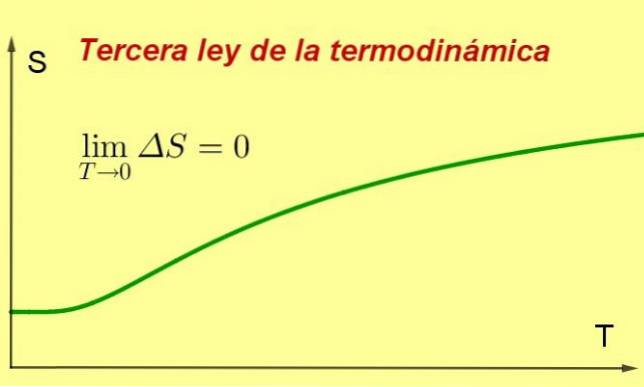
Det Tredje lov om termodynamik siger, at entropien af et lukket termodynamisk system i ligevægt har tendens til at være minimal og konstant, når dets temperatur nærmer sig 0 kelvin.
Denne entropiværdi vil være uafhængig af systemvariablerne (tryk eller anvendt magnetfelt, blandt andre). Hvad der sker er, at når temperaturen er tættere på 0 K, stopper processerne i systemet, og da entropi er et mål for intern agitation, falder det nødvendigvis.
Artikelindeks
- 1 Tidligere begreber
- 1.1 Termodynamisk system
- 1.2 Isolerede, lukkede eller åbne systemer
- 1.3 Makrostater og mikrostater
- 2 Formler og ligninger
- 2.1 Beregning af et stofs absolutte entropi
- 3 applikationer
- 3.1 Entropi af et system ved lav temperatur
- 3.2 Rest entropi
- 4 eksempler
- 4.1 Eksempel 1: absolut nul og Heisenbergs ubestemmelighed
- 4.2 Eksempel 2: Superfluiditet og det mærkelige tilfælde af helium-4
- 5 Øvelser løst
- 5.1 - Øvelse 1
- 5.2 - Øvelse 2
- 6 Referencer
Tidligere begreber
For at forstå omfanget af den tredje lov om termodynamik, der er relevant ved meget lave temperaturer, er det nødvendigt at gennemgå følgende begreber:
Termodynamisk system
Henviser generelt til en gas, en væske eller et fast stof. Hvad der ikke er en del af systemet kaldes miljø. Det mest almindelige termodynamiske system er den ideelle gas, som består af N-partikler (atomer), der kun interagerer gennem elastiske kollisioner.
Isolerede, lukkede eller åbne systemer
Isolerede systemer tillades ikke nogen udveksling med miljøet. Lukkede systemer udveksler ikke noget med miljøet, men de udveksler varme. Endelig kan åbne systemer udveksle både stof og varme med miljøet..
Makrostater og mikrostater
Makrotilstanden i et system er det sæt af værdier, som dets variabler har: tryk, temperatur, volumen, antal mol, entropi og intern energi. På den anden side gives mikrostaten - i tilfælde af en ideel gas - positionen og momentum for hver af de N-partikler, der udgør den, på et givet øjeblik.
Mange mikrostater kan resultere i den samme makrostat. I en gas ved stuetemperatur er antallet af mulige mikrostater enormt, fordi antallet af partikler, der udgør den, de forskellige positioner og de forskellige energier, de kan indtage, er meget stort..
Formler og ligninger
Entropi, som vi sagde, er en termodynamisk makroskopisk variabel, der måler graden af molekylær lidelse i systemet. Graden af forstyrrelse i et system er større, da antallet af mulige mikrostater er større.
Dette koncept er nødvendigt for at formulere den tredje lov om termodynamik i matematisk form. Lad S være systemets entropi, så:

Entropi er en makroskopisk tilstandsvariabel, der er direkte relateret til antallet af mulige mikrostater i et system gennem følgende formel:
S = k ln (W)
I ovenstående ligning: S repræsenterer entropi, W antallet af mulige mikrostater i systemet og k er Boltzmanns konstant (k = 1,38 x 10-2. 3 J / K). Det vil sige, at et systems entropi er k gange den naturlige logaritme for antallet af mulige mikrostater.
Beregning af et stofs absolutte entropi
Det er muligt at definere den absolutte entropi af et rent stof startende med definitionen af entropi-variationen:

δQ = n. cs .dT
Her er cp den molære specifikke varme og n antallet af mol. Afhængigheden af molær specifik varme med temperaturen er data opnået eksperimentelt og kendt for mange rene stoffer..
I henhold til den tredje lov om rene stoffer:


Ansøgninger
I hverdagen har den tredje lov om termodynamik få anvendelser, snarere det modsatte af den første og anden lov. Det er fordi det er et princip, der refererer til, hvad der sker i et system, når det nærmer sig absolut 0, et sjældent temperaturinterval.
Faktisk er det umuligt at nå absolut 0 eller -273,15 ° C (se eksempel 1 nedenfor). Den tredje lov gælder imidlertid, når man studerer materialers reaktion ved meget lave temperaturer.
Takket være dette er der kommet vigtige fremskridt inden for kondenseret fysiks fysik, såsom:
-Superfluiditet (se eksempel 2 nedenfor)
-Superledningsevne
-Laser køling teknikker
-Bose-Einstein kondensat
-Fermi superfluidgasser.

Ved ekstremt lave temperaturer tillader faldet i entropi fremkomsten af interessante kvantefænomener. Lad os derfor se, hvad der sker med et systems entropi ved meget lav temperatur.
Entropi af et system ved lav temperatur
Når du har et perfekt krystallinsk stof, er dets minimale entropi nøjagtigt nul, da det er et meget ordnet system. Ved temperaturer tæt på absolut 0 er stof i kondenseret tilstand (flydende eller fast), og vibrationer i krystallen er minimale.
Nogle forfattere overvejer en alternativ erklæring af den tredje lov om termodynamik som følger:
"Hvis stof kondenserer til dannelse af en perfekt krystal, når temperaturen har en tendens til absolut nul, har entropien en tendens til nøjagtigt nul".
Lad os præcisere nogle aspekter af den foregående erklæring:
- En perfekt krystal er en, hvor hvert molekyle er identisk, og hvor molekylstrukturen gentager sig identisk i sin helhed..
- Når temperaturen nærmer sig absolut nul, falder atomvibrationen næsten fuldstændigt.
Derefter danner krystallen en enkelt konfiguration eller mulig mikrostat, det vil sige W = 1, og derfor er entropien lig med nul:
S = k ln (1) = 0
Men det er ikke altid, at et materiale afkølet nær absolut nul danner en krystal, meget mindre er denne krystal perfekt. Dette sker kun, hvis køleprocessen er meget langsom og reversibel..
Ellers ville faktorer som urenheder til stede i glasset muliggøre eksistensen af andre mikrostater. Derfor ville W> 1 og entropien være større end 0.
Rest entropi
Hvis køleprocessen er brat, gennemgår systemet en række af ikke-ligevægtstilstande, som fører til, at materialet bliver forglasset. I dette tilfælde produceres der ikke en ordnet krystallinsk struktur, men et amorft fast stof, hvis struktur svarer til en væskes struktur..
I så fald er den minimale entropiværdi i nærheden af absolut nul ikke nul, da antallet af mikrostater er betydeligt større end 1. Forskellen mellem denne entropi og nul entropi i den perfekte krystallinske tilstand er kendt som resterende entropi.
Forklaringen er, at systemet under en bestemt tærskelstemperatur ikke har nogen anden mulighed end at optage mikrostaterne med lavere energi, som, fordi de er kvantificeret, udgør et fast antal.
De sørger for at holde entropien konstant, selv når temperaturen fortsætter med at falde mod absolut nul..
Eksempler
Eksempel 1: absolut nul og Heisenbergs ubestemmelighed
Heisenbergs princip om ubestemmelighed fastslår, at usikkerheden i en partikels position og momentum, for eksempel i atomerne i et krystalgitter, ikke er uafhængige af hinanden, men snarere følger følgende ulighed:
Δx ⋅ Δp ≥ h
Hvor h er Plancks konstant. Det vil sige, at usikkerheden i position ganget med usikkerheden i momentum (masse gange hastighed) er større end eller lig med Plancks konstant, hvis værdi er meget lille, men ikke nul: h = 6,63 x 10-3. 4 J s.
Og hvad har usikkerhedsprincippet at gøre med den tredje lov om termodynamik? Hvis atomernes position i krystalgitteret er fast og præcis (Δx = 0) så kan hastigheden på disse atomer tage enhver værdi mellem 0 og uendelig. Dette modsiges af det faktum, at al bevægelse af termisk omrøring ophører ved absolut nul..
Gensidigt, hvis vi antager, at ved absolut nul temperatur ophører al omrøring, og momentet for hvert atom i gitteret er nøjagtigt nul (Δp = 0), så ville Heisenberg usikkerhedsprincippet antyde, at ubestemmelighed i hvert atoms positioner ville være uendelig, dvs. de kan være i enhver position.
Som en konsekvens af den foregående erklæring ville antallet af mikrostater have en tendens til uendelig, og entropien ville også tage en ubestemt værdi.
Eksempel 2: Superfluiditet og det mærkelige tilfælde af helium-4
I overflødighed, der forekommer ved meget lave temperaturer, mister stof den indre friktion mellem dets molekyler, kaldet viskositet. I et sådant tilfælde kunne væsken cirkulere uden friktion for evigt, men problemet er ved disse temperaturer næsten intet er flydende undtagen helium..
Helium og helium 4 (dens mest rigelige isotop) udgør et unikt tilfælde, da helium forbliver flydende ved atmosfærisk tryk og ved temperaturer tæt på absolut nul..
Når helium-4 udsættes for en temperatur under 2,2 K ved atmosfærisk tryk, bliver det til en superfluid. Denne opdagelse fandt sted i 1911 i Leyden af den hollandske fysiker Heike Kamerlingh Onnes (1853-1926).
Helium-4-atomet er et boson. Bosoner, i modsætning til fermioner, er partikler, der alle kan indtage den samme kvantetilstand. Derfor opfylder bosoner ikke Pauli-udelukkelsesprincippet.
Derefter besætter alle helium-4-atomer ved temperaturer under 2,2 K den samme kvantetilstand, og derfor er der kun en mulig mikrostat, hvilket antyder, at superfluid helium-4 har S = 0.
Løst øvelser
- Øvelse 1
Lad os overveje en simpel sag, der består af et system, der kun består af tre partikler, der har tre energiniveauer. Til dette enkle system:
a) Bestem antallet af mulige mikrostater for tre temperaturområder:
-høj
-Halvt
-Kort
b) Bestem ved hjælp af Boltzmann-ligningen entropien i de forskellige temperaturområder.
c) Diskuter resultaterne og forklar, om de er i modstrid med den tredje lov om termodynamik..
Løsning til
På molekylær og atomskala kvantificeres de energier, som et system kan optage, hvilket betyder, at de kun kan tage bestemte diskrete værdier. Når temperaturen er så lav, har de partikler, der udgør systemet, kun muligheden for at optage de laveste energiniveauer..
Høj temperatur
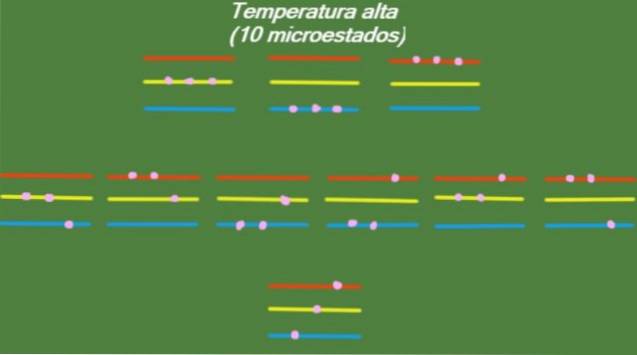
Hvis systemet har en relativt høj temperatur T, har partiklerne nok energi til at optage eventuelle tilgængelige niveauer, hvilket giver anledning til 10 mulige mikrostater, som vises i følgende figur:
Medium temperatur
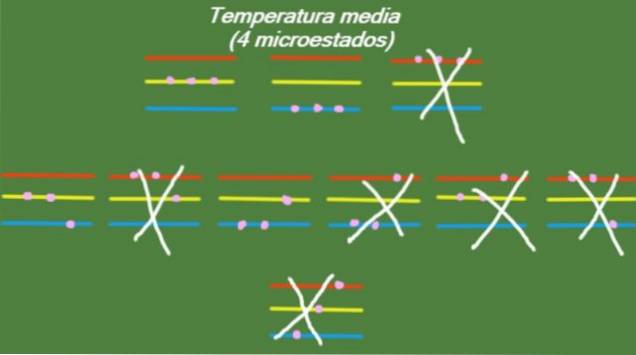
I tilfælde af at systemet har en mellemtemperatur, har partiklerne, der udgør det, ikke nok energi til at optage det højeste energiniveau. De mulige mikrostater er illustreret i figuren:
Lav temperatur
Hvis temperaturen fortsætter med at falde i vores idealiserede system med tre partikler og tre energiniveauer, vil partiklerne have så lidt energi, at de kun vil kunne indtage det laveste niveau. I dette tilfælde er der kun 1 mulig mikrostat, som vist i figur 6:
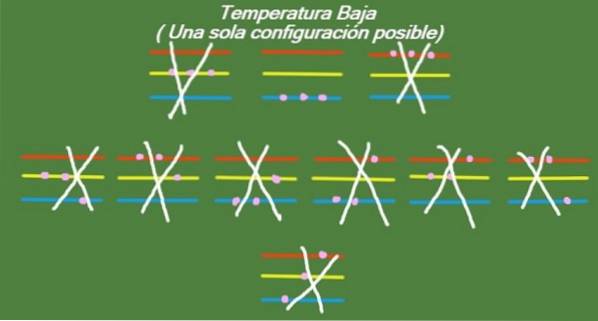
Løsning b
Når antallet af mikrostater i hvert temperaturområde er kendt, kan vi nu bruge Boltzmann-ligningen ovenfor til at finde entropien i hvert tilfælde.
S = k ln (10) = 2,30 x k = 3,18 x 10-2. 3 J / K (Høj temperatur)
S = k ln (4) = 1,38 x k = 1,92 x 10-2. 3 J / K (Medium temperatur)
Og endelig:
S = k ln (1) = 0 (Lav temperatur)
Løsning c
Først bemærker vi, at entropien falder, når temperaturen falder som forventet. Men for de laveste temperaturværdier nås en tærskelværdi, hvorfra systemets basistilstand nås..
Selv når temperaturen er så tæt på absolut nul som muligt, er der ingen tilgængelige energitilstande til rådighed. Derefter holder entropien sin minimumsværdi konstant, som i vores eksempel er S = 0.
Denne øvelse illustrerer, på et mikrostatsniveau i et system, årsagen til, at den tredje lov om termodynamik holder..
- Øvelse 2
Årsag, hvis følgende udsagn er sand eller falsk:
"Entropi af et system ved absolut nul temperatur er nøjagtigt nul".
Begrund dit svar og beskriv nogle eksempler.
Opløsning
Svaret er: falsk.
For det første kan den absolutte 0 temperatur ikke nås, fordi det ville være i strid med Heisenbergs usikkerhedsprincip og den tredje lov om termodynamik..
Det er meget vigtigt at bemærke, at den tredje lov ikke siger, hvad der sker ved absolut 0, men snarere når temperaturen er uendeligt tæt på absolut 0. Forskellen er subtil, men signifikant.
Den tredje lov bekræfter heller ikke, at når temperaturen tager en værdi vilkårligt tæt på absolut nul, har entropien en tendens til nul. Dette ville kun forekomme i det tidligere analyserede tilfælde: den perfekte krystal, som er en idealisering.
Mange systemer i mikroskopisk skala, det vil sige i kvanteskala, har deres basisniveau af energi degenererede, hvilket betyder eksistensen af forskellige indstillinger på det laveste energiniveau.
Det betyder, at entropien i disse systemer aldrig ville være nøjagtigt nul. Entropien ville heller ikke være nøjagtigt nul i systemer, der forglasses, når temperaturen har en tendens til absolut nul. I dette tilfælde er resterende entropi før set.
Det skyldes, at dets molekyler blev "fast", inden de nåede de laveste niveauer af tilgængelig energi, hvilket øger antallet af mulige mikrostater betydeligt, hvilket gør det umuligt for entropien at være nøjagtigt nul..
Referencer
- Cengel, Y. 2012. Termodynamik. 7. udgave. McGraw Hill. 347.
- Jet Propulsion Laboratory. Det fedeste sted i universet. Hentet fra: coldatomlab.jpl.nasa.gov.
- González, A. Entropi og spontanitet. Gendannet fra: geocities.ws
- Quora. Hvad er den praktiske anvendelse af tredje lov om termodynamik?. Gendannet fra: quora.com
- Generel kemi. Tredje princip for termodynamik. Gendannet fra: corinto.pucp.edu.pe
- Tredje lov om termodynamik. Gendannet fra: youtube.com
- Wikipedia. Rest entropi. Gendannet fra: en.wikipedia.com
- Wikipedia. Tredje lov om termodynamik. Gendannet fra: en.wikipedia.com



Endnu ingen kommentarer