Parabolske optagelsesegenskaber, formler og ligninger, eksempler

Det parabolsk skud Det består i at kaste et objekt eller projektil i en bestemt vinkel og lade det bevæge sig under tyngdekraftens virkning. Hvis luftmodstand ikke tages i betragtning, vil objektet, uanset dets natur, følge en parabelbue.

Det er en daglig bevægelse, da blandt de mest populære sportsgrene er dem, hvor kugler eller bolde kastes, enten med hånden, med foden eller med et instrument som f.eks. En ketcher eller en flagermus.

Til sin undersøgelse opdeles det parabolske skud i to overlejrede bevægelser: den ene vandret uden acceleration og den anden lodret med konstant nedadgående acceleration, hvilket er tyngdekraften. Begge bevægelser har starthastighed.

Lad os sige, at den vandrette bevægelse løber langs x-aksen og den lodrette bevægelse langs y-aksen. Hver af disse bevægelser er uafhængige af den anden.

Da bestemmelse af projektilets position er hovedformålet, er det nødvendigt at vælge et passende referencesystem. Detaljer er nedenfor.

Artikelindeks

• 1 Paraboliske skudformler og ligninger
  • 1.1 - Bane, maksimal højde, maksimal tid og vandret rækkevidde
• 2 Eksempler på parabolsk skydning
  • 2.1 Parabolskydning i menneskelige aktiviteter
  • 2.2 Det parabolske skud i naturen
• 3 Træning
• 4 Referencer

Paraboliske skudformler og ligninger

Antag, at objektet kastes med vinkel α i forhold til den vandrette og indledende hastighed v_eller som vist i figuren til venstre. Det parabolske skud er en bevægelse, der finder sted på flyet xy og i så fald nedbrydes starthastigheden sådan:

v_okse = v_eller cos α

v_Hej = v_eller sin α

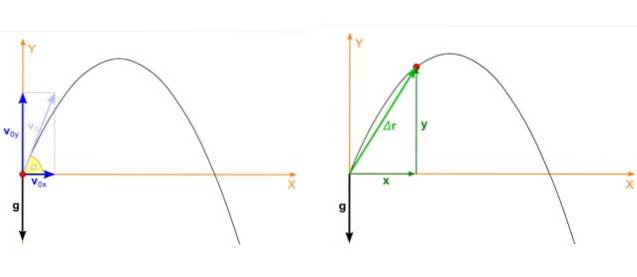
Projektilets position, som er den røde prik i figur 2, højre billede, har også to tidsafhængige komponenter, en i x og den anden i Y. Position er en vektor betegnet som r og dens enheder er længde.

I figuren falder projektilens startposition sammen med koordinatsystemets oprindelse, derfor x_eller = 0 og_eller = 0. Dette er ikke altid tilfældet, du kan vælge oprindelsen hvor som helst, men dette valg forenkler beregningerne meget.

Hvad angår de to bevægelser i x og i y, er disse:

-x (t): er en ensartet lodret bevægelse.

-y (t): svarer til en ensartet accelereret retlinet bevægelse med g = 9,8 m / s^to og peger lodret nedad.

I matematisk form:

x (t) = v_eller cos α.t

y (t) = v_eller .sin α.t - ½g.t^to

Positionsvektoren er:

r (t) = [v_eller cos α.t]jeg + [v_eller .sin α.t - ½g.t^to] j

I disse ligninger vil den opmærksomme læser bemærke, at minustegnet skyldes tyngdekraften, der peger mod jorden, den valgte retning er negativ, mens opadgående tages som positiv..

Da hastighed er det første afledte af position, skal du blot udlede r (t) med hensyn til tid og opnå:

v (t) = v_eller cos α jeg + (v_eller .sin α - gt) j

Endelig udtrykkes accelerationen vektorielt som:

til (t) = -g j

- Bane, maksimal højde, maksimal tid og vandret rækkevidde

Bane

For at finde den eksplicitte ligning af stien, som er kurven y (x), skal vi eliminere tidsparameteren, løse i ligningen for x (t) og erstatte i y (t). Forenklingen er lidt besværlig, men til sidst får du:

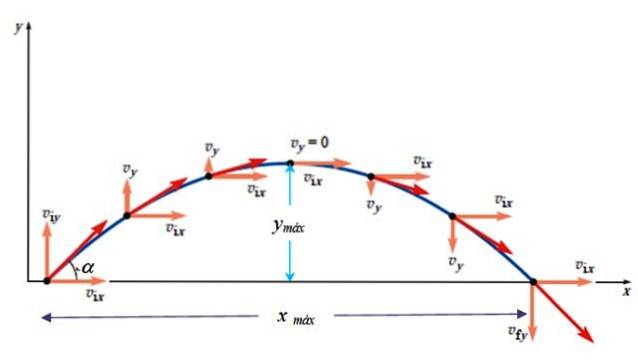
Maksimal højde

Den maksimale højde opstår, når v_Y = 0. At vide, at der er følgende forhold mellem position og kvadratet af hastigheden:

v_Y^to = v_Hej ^to- 2gy

Gør v_Y = 0 lige når man når den maksimale højde:

0 = v_Hej ^to- 2g. Og_maks → og_maks = v_Hej ^to/ 2 g

Med:

v_Hej = v_eller sena

Maksimal tid

Den maksimale tid er den tid, det tager for objektet at nå og_maks. For at beregne det bruges:

v_Y = v_eller .sin α - gt

At vide det v_Y bliver 0 når t = t_maks, resultat:

v_eller .sin α - g.t_maks = 0

t_maks = v_Hej / g

Maksimal vandret rækkevidde og flyvetid

Området er meget vigtigt, fordi det signalerer, hvor objektet vil falde. På denne måde ved vi, om det rammer målet eller ej. For at finde det har vi brug for flyvetid, total tid eller t_v.

Fra ovenstående illustration er det let at konkludere det t_v = 2.t_maks. Men pas på! Dette gælder kun, hvis lanceringen er plan, dvs. startpunktets højde er den samme som ankomsthøjden. Ellers findes tiden ved at løse den kvadratiske ligning, der er resultatet af at erstatte den endelige position Y_endelig:

Y_endelig = v_eller .sin α.t_v - ½g.t_v^to

Under alle omstændigheder er den maksimale vandrette rækkevidde:

x_maks = v_okse. t_v

Eksempler på parabolsk skydning

Parabolskydning er en del af bevægelsen af ​​mennesker og dyr. Også af næsten alle sportsgrene og spil, hvor tyngdekraften griber ind. For eksempel:

Parabolsk skydning i menneskelige aktiviteter

-Stenen kastet af en katapult.

-Målmandens målspark.

-Bolden kastet af kanden.

-Pilen, der kommer ud af buen.

-Alle slags spring

-Kast en sten med et slynge.

-Ethvert kastet våben.

Det parabolske skud i naturen

-Vand, der strømmer ud af naturlige eller kunstige stråler, såsom dem fra et springvand.

-Sten og lava strømmer ud af en vulkan.

-En kugle, der springer op fra fortovet eller en sten, der hopper på vandet.

-Alle slags springende dyr: kænguruer, delfiner, gazeller, katte, frøer, kaniner eller insekter, for at nævne nogle få.

Dyrke motion

En græshoppe hopper i en vinkel på 55º med vandret og lander 0,80 meter foran. Finde:

a) Den maksimale højde, der er nået.

b) Hvis han sprang med den samme starthastighed, men dannede en vinkel på 45º, ville han gå højere??

c) Hvad kan man sige om den maksimale vandrette rækkevidde for denne vinkel?

Løsning til

Når de data, der leveres af problemet, ikke indeholder starthastigheden v_eller beregningerne er noget mere besværlige, men fra de kendte ligninger kan et nyt udtryk udledes. Startende fra:

x_maks = v_okse . t_flyvningen = v_eller.cos α. t_v

Når det lander senere, vender højden tilbage til 0, så:

v_eller .sin α.t_v - ½g.t_v^to= 0

Hvad t_v er en fælles faktor, det er forenklet:

v_eller .sin α - ½g.t_v= 0

Vi kan rydde t_v fra den første ligning:

t_v = x_maks / v_eller.cos α

Og udskift i det andet:

v_eller .sin α - (½g.x_maks / v_eller.cos α) = 0

Ved at multiplicere alle termerne med v_eller.cos αudtrykket ændres ikke, og nævneren forsvinder:

(v_eller .sin α.) (v_eller.cos α) - ½g.x_maks = 0

v_eller^to sin α. cos α = ½g.x_maks

Det kan allerede være ryddet v_eller eller også erstatte følgende identitet:

sin 2α = 2 sin α. cos α → v_eller^to sin 2α = g.x_maks

Beregnes v_eller^to:

v_eller^to = g.x_maks / sin 2α = (9,8 x 0,8 / sin 110) m^to/ s^to = 8,34 m^to/ s^to

Og endelig den maksimale højde:

Y_maks= v_Hej ^to/ 2g = (8,34 x sin^to 55) / (2 x 9,8) m = 0,286 m = 28,6 cm

Løsning b

Hummeren formår at opretholde den samme vandrette hastighed, men ved at mindske vinklen:

Y_maks= v_Hej ^to/ 2g = (8,34 x sin^to 45) / (2 x 9,8) m = 0,213 m = 21,3 cm

Opnår en lavere højde.

Løsning c

Den maksimale vandrette rækkevidde er:

x_maks = v_eller^to sen 2. / g

Ved at variere vinklen ændres den vandrette rækkevidde også:

x_maks = 8,34 sen 90 / 9.8  m = 0,851 m = 85,1 cm

Springet er længere nu. Læseren kan kontrollere, at det er maksimalt for 45 ° vinklen, fordi:

sin 2α = sin 90 = 1.

Referencer

1. Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB).
2. Giambattista, A. 2010. Fysik. Anden version. Mcgraw bakke.
3. Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
4. Resnick, R. 1999. Fysik. Bind 1. 3. udgave på spansk. Compañía Editorial Continental S.A. af C.V.
5. Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.