
Bane i fysiske egenskaber, typer, eksempler og øvelser
Det bane i fysik Det er kurven, som en mobil beskriver, når den passerer på hinanden følgende punkter under dens bevægelse. Da det kan vedtage et uendeligt antal varianter, vil banerne, som mobilen kan følge, også gøre.
For at komme fra et sted til et andet kan en person tage forskellige stier og forskellige måder: til fods gennem fortovene i gader og alléer eller ved at ankomme i bil eller motorcykel på en motorvej. Under en tur gennem skoven kan vandreren følge en kompliceret sti, der inkluderer sving, gå op eller ned i niveau og endda passere gennem det samme punkt flere gange.
Hvis de punkter, som mobilen kører igennem, følger en lige linje, vil banen være retlinet. Dette er den enkleste vej, fordi den er endimensionel. For at specificere positionen kræves en enkelt koordinat.
Men mobilen kan følge en krøllet sti, være i stand til at være lukket eller åben. I disse tilfælde kræver sporing af positionen to eller tre koordinater. Dette er bevægelser i henholdsvis planet og i rummet. Dette har at gøre med links: materielle forhold, der begrænser bevægelse. Nogle eksempler er:
- Banerne, der beskriver planeterne omkring solen, er lukkede ellipseformede stier. Selv om de i nogle tilfælde kan tilnærmes til et cirkulær, som det er tilfældet med Jorden.
- Bolden, som målmanden sparker i et målspark, følger en parabolsk bane.
- En fugl i flugt beskriver krumlinjeformede baner i rummet, for ud over at flytte på et fly kan den også gå op eller ned i niveau efter ønske.
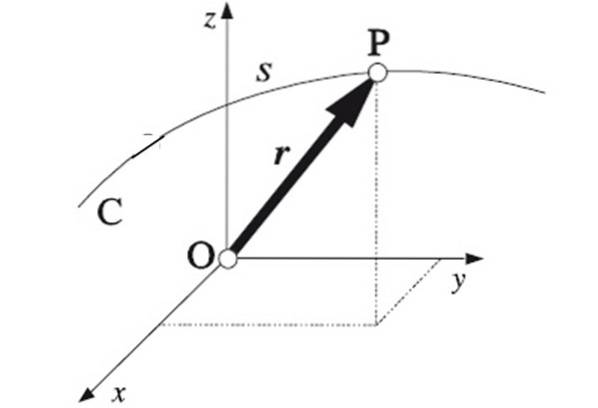
Banen i fysik kan udtrykkes matematisk, når mobilens position er kendt på ethvert tidspunkt. Være r positionsvektoren, som igen har koordinater x, Y Y z i det mest generelle tilfælde af en bevægelse i tre dimensioner. Kendskab til funktionen r (t) banen bestemmes fuldstændigt.
Artikelindeks
- 1 Typer
- 1.1 Bevægelser i en, to og tre dimensioner
- 2 Eksempler
- 2.1 Mobilens sti på en eksplicit, implicit og parametrisk måde
- 3 Løst øvelser
- 3.1 Løst øvelse 1
- 3.2 Øvelse løst 2
- 3.3 Øvelse løst 3
- 4 Referencer
Typer
Generelt kan banen være en ret kompliceret kurve, især hvis du vil udtrykke den matematisk. Af denne grund begynder det med de enkleste modeller, hvor mobiltelefoner kører på en lige linje eller på et plan, som kan være gulvet eller en hvilken som helst anden passende:
Bevægelser i en, to og tre dimensioner
De mest undersøgte baner er:
- Retlinet, når du kører på en lige vandret, lodret eller skrå linje. En kugle kastet lodret op følger denne sti, eller en genstand, der glider ned ad en hældning følger. De er endimensionelle bevægelser, en enkelt koordinat er nok til at bestemme deres position fuldstændigt..
- Parabolsk, hvor mobilen beskriver en bue af en parabel. Det er hyppigt, da ethvert objekt, der smides skråt under tyngdekraftens virkning (et projektil) følger denne bane. For at specificere mobilens position skal du angive to koordinater: x Y Y.
- Cirkulær, opstår, når den bevægelige partikel følger en cirkel. Det er også almindeligt i naturen og i den daglige praksis. Mange hverdagsgenstande følger en cirkulær sti som dæk, maskindele og satellitter i kredsløb for at nævne nogle få..
- Elliptisk, objektet bevæger sig efter en ellipse. Som sagt i starten er det stien, der følges af planeterne i kredsløb omkring solen.
- Hyperbolisk, Astronomiske objekter under påvirkning af en central kraft (tyngdekraft) kan følge elliptiske (lukkede) eller hyperbolske (åbne) baner, disse er mindre hyppige end de tidligere.
- Spiralformet, eller spiralbevægelse, som for en fugl, der stiger op i en termisk strøm.
- Sving eller pendul, mobilen beskriver en bue i frem og tilbage bevægelser.
Eksempler
Banerne beskrevet i det foregående afsnit er meget nyttige til hurtigt at få en idé om, hvordan et objekt bevæger sig. Under alle omstændigheder er det nødvendigt at præcisere, at banen til en mobil afhænger af placeringen af observatøren. Dette betyder, at den samme begivenhed kan ses på forskellige måder, afhængigt af hvor hver person er..
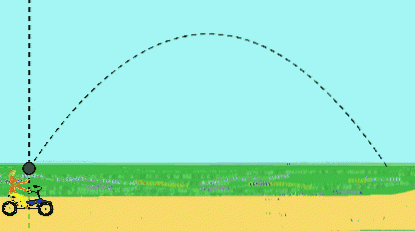
For eksempel pedaler en pige med konstant hastighed og kaster en kugle opad. Hun bemærker, at bolden beskriver en retlinet sti.
For en observatør, der står på vejen, der ser den passere, vil bolden imidlertid have en parabolsk bevægelse. For ham blev bolden oprindeligt kastet med en skrå hastighed, et resultat af hastigheden opad af pigens hånd plus cykelens hastighed..
Mobilens sti på en eksplicit, implicit og parametrisk måde
- Eksplicit, direkte angive kurven eller locus givet af ligningen y (x)
- Implicit, hvor en kurve udtrykkes som f (x, y, z) = 0
-Parametrisk, i denne form gives x-, y- og z-koordinaterne som en funktion af en parameter, der generelt vælges som tid t. I dette tilfælde består banen af funktionerne: x (t), og T) Y z (t).
Dernæst er to baner, der er blevet undersøgt bredt inden for kinematik, detaljerede: den parabolske bane og den cirkulære bane..
Vippet start i vakuum
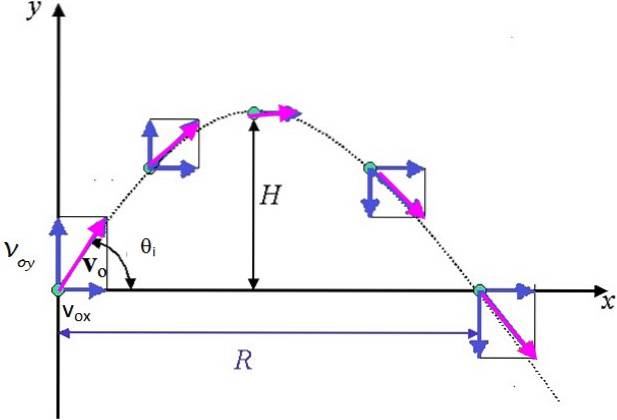
Et objekt (projektilet) smides i en vinkel a med vandret og med starthastighed veller som billedet viser. Luftmodstand tages ikke i betragtning. Bevægelsen kan behandles som to uafhængige og samtidige bevægelser: den ene vandret med konstant hastighed og den anden lodret under tyngdekraftens virkning..
x (t) = xeller +vokse.t
y (t) = yeller +vHej.t -½g.tto
Disse ligninger er parametriske ligninger lancering af projektil. Som forklaret ovenfor har de parameteren t, Hvad er klokken.
Følgende kan ses i den højre trekant i figuren:
vokse = veller cos θjeg
vHej = veller sen θjeg
Udskiftning af disse ligninger indeholdende startvinklen i de parametriske ligninger resulterer i:
x (t) = xeller +veller cos θjeg.t
y (t) = yeller +veller. sen θjeg.t -½g.tto
Ligning af den parabolske vej
Den eksplicitte ligning af stien findes ved at løse t fra ligningen for x (t) og erstatte i ligningen med y (t). For at lette algebraisk arbejde kan det antages, at oprindelsen (0,0) er placeret ved startpunktet og dermed xeller = ogeller = 0.
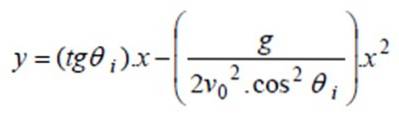
Dette er ligningen af stien i eksplicit måde.
Cirkulær sti
En cirkulær sti er givet ved:
(x - xeller)to + (og - ogeller)to = Rto

Her xeller og ogeller repræsenterer centrum for den cirkel, der er beskrevet af mobilen, og R er dens radius. P (x, y) er et punkt på stien. Fra den skyggefulde højre trekant (figur 3) kan det ses, at:
x = R. cos θ
y = R. sin θ
Parameteren er i dette tilfælde den fejede vinkel θ, kaldet vinkelforskydning. I det særlige tilfælde, at vinkelhastigheden ω (vinkel fejet pr. Tidsenhed) er konstant, kan det siges, at:
θ = θeller + ωt
Hvor θeller er den indledende vinkelposition for partiklen, som, hvis den tages som 0, reduceres til:
θ = ωt
I et sådant tilfælde vender tiden tilbage til parametriske ligninger som:
x = R.cos ωt
y = R. sin ωt
Enhedsvektorerne jeg Y j er meget praktiske til at skrive et objekts positionsfunktion r (t). De angiver retningerne på aksen x og på aksen Y henholdsvis. I dets termer er placeringen af en partikel, der beskriver en ensartet cirkulær bevægelse:
r (t) = R.cos ωt jeg + R. sen ωt j
Løst øvelser
Løst øvelse 1
En kanon kan affyre en kugle med en hastighed på 200 m / s og en vinkel på 40 ° i forhold til vandret. Hvis kastet er på fladt underlag, og luftmodstand forsømmes, skal du finde:
a) Stigningens ligning y (x) ...
b) Parametriske ligninger x (t) Y og T).
c) Det vandrette område og den tid projektilet varer i luften.
d) Projektilets højde er når x = 12.000 m
Løsning til)
a) For at finde banen erstattes værdierne i ligningen y (x) i det foregående afsnit:
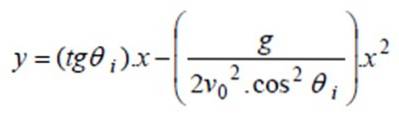
y (x) = tg 40º. x - 9.8 / (2 '400to. costo40.) xto ⇒ y (x) = 0,8391 x - 0,0000522xto
Løsning b)
b) Startpunktet vælges ved koordinatsystemets oprindelse (0,0):
x (t) = xeller +vokse.t = 400'cos 40º.t = 306,42. t.
y (t) = yeller +vHej.t -½g.tto= 400 'sin 40º.t - 0.5 '9.8'tto= 257,12 t - 4,9.tto
Løsning c)
c) For at finde den tid projektilet holder i luften y (t) = 0, at være lanceringen er lavet på flad jord:
0 = 257.12.t - 4.9.tto
t = 257,12 / 4,9 s = 52,473 s
Den maksimale vandrette rækkevidde findes ved at erstatte denne værdi i x (t):
xmaks = 306,42'52, 47 m = 16077,7 m
En anden måde at finde x påmaks direkte er ved at lave y = 0 i ligning af stien:
0 = 0,8391 xmaks - 0,0000522 xtomaks
x = 0,8391 / 0,0000522 m = 16078,5 m
Der er en lille forskel på grund af afrunding af decimaler.
Løsning d)
d) For at finde højden, når x = 12000 m, erstattes denne værdi direkte i ligning af stien:
og (12000) = 0,8391'12000 - 0,000052212000to m = 2552,4 m
Træning løst 2
Positionsfunktionen for et objekt er givet ved:
r (t) = 3t jeg + (4 -5tto) j m
Finde:
a) Ligningen for stien. Hvad kurve er?
b) Startposition og position når t = 2 s.
c) Forskydningen foretaget efter t = 2 s.
Opløsning
a) Positionsfunktionen er givet i form af enhedsvektorerne jeg Y j, som henholdsvis bestemmer retningen på akserne x Y Y, Dermed:
x (t) = 3t
og T) = 4 -5tto
Stigens ligning y (x) rydder t fra x (t) og erstatte i y (t):
t = x / 3
y (x) = 4-5. (x / 3)to = 4-5 gangeto/ 9 (lignelse)
b) Udgangspositionen er: r (2) = 4 j m ; positionen i t = 2 s det er r (2) = 6 jeg -16 j m
c) Forskydning Dr er subtraktion af de to positionsvektorer:
Δr = r (to) - r (2) = 6 jeg -16 j- 4 j = 6 jeg - tyve j m
Træning løst 3
Jorden har en radius R = 6300 km, og det er kendt, at rotationsperioden for dens bevægelse omkring sin akse er en dag. Finde:
a) Ligningen for et punkt på jordens overflade og dets positionsfunktion.
b) Hastigheden og accelerationen af dette punkt.
Løsning til)
a) Positionsfunktionen for ethvert punkt i cirkulær bane er:
r (t) = R.cos ωt jeg + R.sen ωt j
Vi har jordens radius R, men ikke vinkelhastigheden ω, men den kan beregnes ud fra perioden, idet vi ved, at det for cirkulær bevægelse er gyldigt at sige, at:
ω = 2π × frekvens = 2π / periode
Bevægelsesperioden er: 1 dag = 24 timer = 1440 minutter = 86400 sekunder, derfor:
ω = 2π / 86400 s = 0,000023148 s-1
Udskiftning i positionsfunktionen:
r (t) = R.cos ωt jeg + R. sen ωt j = 6300 (cos 0,000023148t jeg + sen 0,000023148t j) Km
Stien i parametrisk form er:
x (t) = 6300. cos 0.000023148t
y (t) = 6300. sin 0,000023148t
Løsning b)
b) For cirkulær bevægelse, størrelsen af den lineære hastighed v af et punkt er relateret til vinkelhastigheden w igennem:
v = ωR = 0,000023148 s-1'6300 Km = 0,1445 Km / s = 145,8 m / s
Selv at være en bevægelse med konstant hastighed på 145,8 m / s, der er en acceleration, der peger mod midten af den cirkulære bane med ansvar for at holde punktet i rotation. Det er den centripetale acceleration tilc, givet af:
tilc = vto / R = (145,8 m / s)to / 6300 × 103 m = 0,00337 m / sto.
Referencer
- Giancoli, D. Fysik. (2006). Principper med applikationer. 6th Prentice Hall. 22-25.
- Kirkpatrick, L. 2007. Fysik: Et blik på verden. 6ta Forkortet udgave. Cengage læring. 23 - 27.
- Resnick, R. (1999). Fysisk. Bind 1. tredje udgave på spansk. Mexico. Compañía Editorial Continental S.A. de C.V. 21-22.
- Rex, A. (2011). Grundlæggende om fysik. Pearson. 33 - 36
- Sears, Zemansky. (2016). Universitetsfysik med moderne fysik. 14th. Red. Bind 1. 50 - 53.
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. 7mor. Udgave. Mexico. Cengage Learning Editors. 23-25.
- Serway, R., Vulle, C. (2011). Grundlæggende om fysik. 9na Ed. Cengage Learning. 43 - 55.
- Wilson, J. (2011). Fysik 10. Pearson Education. 133 - 149.



Endnu ingen kommentarer