Det akutte trekanter er dem, hvis tre indre vinkler er spidse vinkler; dvs. målet for hver af disse vinkler er mindre end 90 ° grader. Ved ikke at have nogen ret vinkel har vi, at den Pythagoras sætning ikke holder for denne geometriske figur.
Derfor, hvis vi ønsker at have en form for information om nogen af dens sider eller vinkler, er det nødvendigt at gøre brug af andre sætninger, der giver os mulighed for at få adgang til de nævnte data. De vi kan bruge er sinus sætning og cosinus sætning.
Artikelindeks
Blandt de egenskaber, som denne geometriske figur har, kan vi fremhæve dem, der er givet ved det enkle faktum at være en trekant. Blandt disse har vi:
- En trekant er en polygon, der har tre sider og tre vinkler.
- Summen af de tre indre vinkler er lig med 180 °.
- Summen af to af dens sider er altid større end den tredje.
Lad os som et eksempel se på den følgende trekant ABC. På en generel måde identificerer vi dens sider med et lille bogstav og dets vinkler med et stort bogstav på en sådan måde, at den ene side og dens modsatte vinkel har samme bogstav.
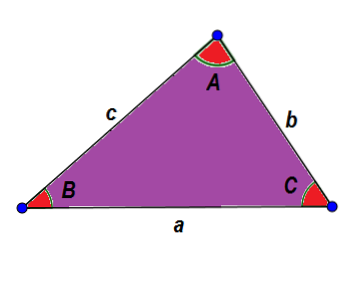
Fra de allerede angivne egenskaber ved vi, at:
A + B + C = 180 °
a + b> c, a + c> b og b + c> a
Hovedkarakteristikken, der adskiller denne type trekant fra resten, er, som vi allerede har nævnt, dens indre vinkler er akutte; det vil sige mål for hver af dens vinkler er mindre end 90 °.
Akutte trekanter er sammen med stumpe trekanter (dem, hvor en af deres vinkler har et mål større end 90 °), en del af sættet med skrå trekanter. Dette sæt består af trekanter, der ikke er rette vinkler.
Da de skrå trekanter er en del, skal vi være i stand til at løse problemer, der involverer akutte trekanter, vi skal gøre brug af sinus sætning og cosinus sætning.
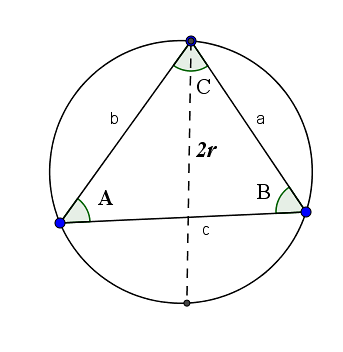
Sinus sætningen fortæller os, at forholdet mellem en side og sinus af dens modsatte vinkel er lig med dobbelt så radius af cirklen, der dannes af de tre hjørner af nævnte trekant. Nemlig:
2r = a / sin (A) = b / sin (B) = c / sin (C)
På den anden side giver cosinus sætningen os disse tre ligheder for enhver trekant ABC:
tilto= bto + cto -2bc * cos (A)
bto= ato + cto -2ac * cos (B)
cto= ato + bto -2ab * cos (C)
Disse sætninger er også kendt som henholdsvis sinusloven og cosinusloven..
Et andet kendetegn, vi kan give af de akutte trekanter, er at to af disse er ens, hvis de opfylder et af følgende kriterier:
- Hvis de har alle tre lige store sider.
- Hvis de har den ene side og to lige store vinkler til hinanden.
- Hvis de har to lige store sider og en vinkel.
Vi kan klassificere akutte trekanter baseret på deres sider. Disse kan være:
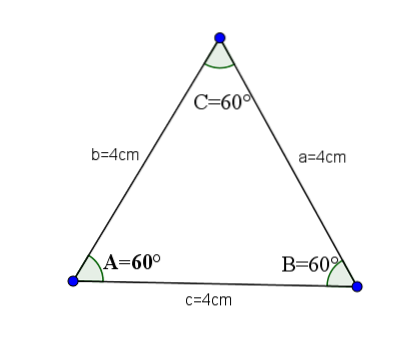
De er de akutte trekanter, der har alle sider lige, og derfor har alle deres indre vinkler den samme værdi, som er A = B = C = 60 ° grader.
Lad os som et eksempel tage følgende trekant, hvis sider a, b og c har en værdi på 4.
Disse trekanter har, ud over at have akutte indre vinkler, karakteristikken ved at have to af deres lige sider og den tredje, som generelt tages som basen, forskellig.
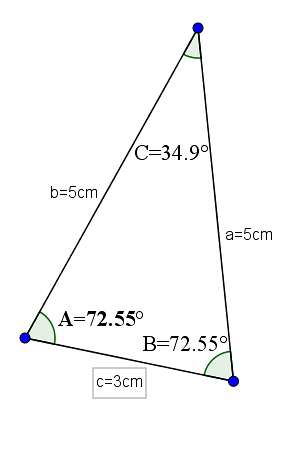
Et eksempel på denne type trekant kan være en, hvis base er 3, og dens andre to sider har en værdi på 5. Med disse målinger ville den have de modsatte vinkler til de lige sider med værdien 72,55 ° og den modsatte vinkel på basen ville være 34,9 °.
Dette er trekanterne, som alle har forskellige sider to og to. Derfor er alle dens vinkler, ud over at være mindre end 90 °, forskellige fra to til to.
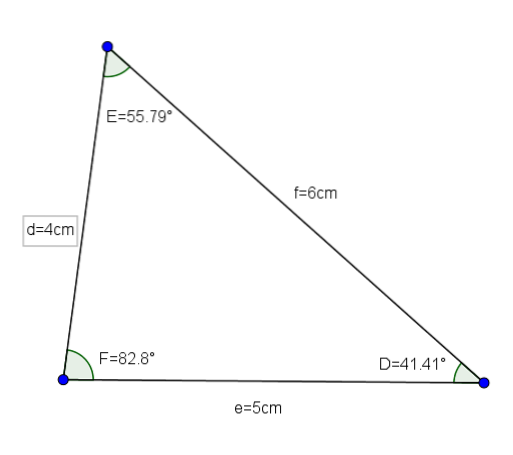
Trekanten DEF (hvis mål er d = 4, e = 5 og f = 6 og dens vinkler er D = 41,41 °, E = 55,79 ° og F = 82,8 °) er et godt eksempel på en akut trekantskala.
Som vi sagde før, for at løse problemer, der involverer akutte trekanter, er det nødvendigt at bruge sinus og cosinus sætninger.
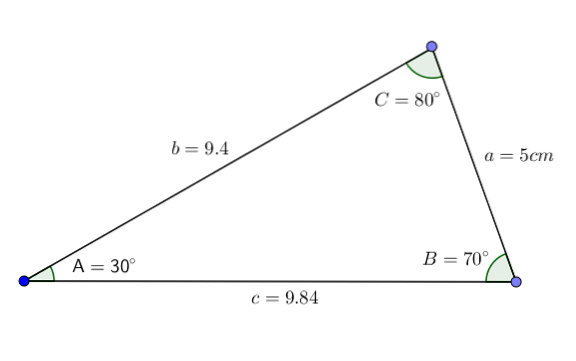
Givet en trekant ABC med vinkler A = 30 °, B = 70 ° og side a = 5 cm, vil vi vide værdien af vinkel C og sider b og c.
Det første vi gør er at bruge det faktum, at summen af de indre vinkler i en trekant er 180 °, for at opnå værdien af vinklen C.
180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C
Vi rydder C, og vi er tilbage med:
C = 180 ° - 100 ° = 80 °
Da vi allerede kender de tre vinkler og den ene side, kan vi bruge sinus sætningen til at bestemme værdien af de resterende sider. Ved sætningen har vi:
a / sin (A) = b / sin (B) og a / sin (A) = c / (sin (C)
Vi isolerer b fra ligningen, og vi er tilbage med:
b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4
Nu behøver vi kun at beregne værdien af c. Vi fortsætter på samme måde som i det foregående tilfælde:
c = (a * sin (C)) / sin (A) ≈ (5 * 0,984) / (0,5) ≈ 9,84
Således får vi alle dataene i trekanten. Som vi kan se, falder denne trekant ind i kategorien scalene akut trekant.
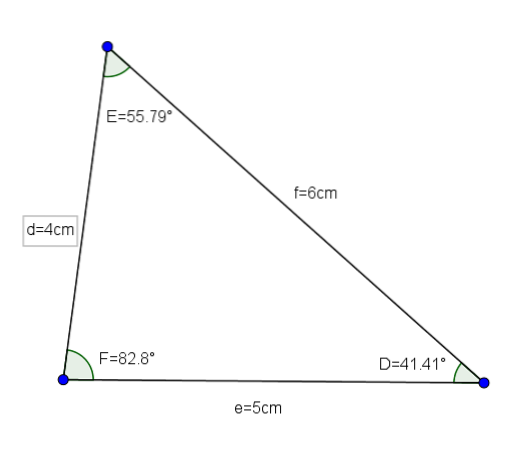
Givet en trekant DEF med siderne d = 4 cm, e = 5 cm og f = 6 cm, vil vi vide værdien af vinklerne i nævnte trekant.
I dette tilfælde vil vi bruge cosinusloven, som fortæller os, at:
dto= eto + Fto - 2efcos (D)
Fra denne ligning kan vi løse for cos (D), hvilket giver os som et resultat:
Cos (D) = ((4)to - (5)to -(6)to) / (- 2 * 5 * 6) = 0,75
Derfor har vi D41,41 °
Nu ved hjælp af senom sætning har vi følgende ligning:
d / (sin (D) = e / (sin (E)
Løsning for synd (E) har vi:
sin (E) = e * sin (D) / d = (5 * 0,66) / 4 ≈ 0,827
Derfor har vi E≈55,79 °
Endelig ved at bruge summen af de indvendige vinkler i en trekant til 180 °, har vi det F≈82.8 °.
Endnu ingen kommentarer