
Ensartede trekantkarakteristika, formel og areal, beregning

EN ligebenet trekant er en polygon med tre sider, hvor to af dem har samme mål og den tredje side et andet mål. Denne sidste side kaldes basen. På grund af denne egenskab fik det dette navn, som på græsk betyder "lige ben"
Trekanter er polygoner, der betragtes som de enkleste i geometri, fordi de består af tre sider, tre vinkler og tre hjørner. Det er dem, der har mindst antal sider og vinkler i forhold til de andre polygoner, men deres anvendelse er meget omfattende.

Artikelindeks
- 1 Kendetegn for ligebenede trekanter
- 1.1 Komponenter
- 2 egenskaber
- 2.1 Indvendige vinkler
- 2.2 Summen af siderne
- 2.3 Kongruente sider
- 2.4 Kongruente vinkler
- 2.5 Højde, median, bisector og bisector er sammenfaldende
- 2.6 Relative højder
- 2.7 Sammenfaldende orthocenter, barycenter, incenter og circumcenter
- 3 Sådan beregnes omkredsen?
- 4 Sådan beregnes højden?
- 5 Sådan beregnes arealet?
- 6 Sådan beregnes bunden af trekanten?
- 7 Øvelser
- 7.1 Første øvelse
- 7.2 Anden øvelse
- 7.3 Tredje øvelse
- 8 Referencer
Karakteristika for ligebenede trekanter
Den ligebenede trekant blev klassificeret ved hjælp af målene på dens sider som en parameter, da to af dens sider er kongruente (de har samme længde).
Baseret på amplituden af de indvendige vinkler klassificeres ligebenede trekanter som:
- Jævnstrøms højre trekant: to af dens sider er ens. En af dens vinkler er rigtig (90eller) og de andre er de samme (45eller hver)
- Jævnslange stumpe trekant: to af dens sider er ens. En af dens vinkler er stump (> 90eller).
- Ensartet akut trekant: to af dens sider er ens. Alle dens vinkler er skarpe (< 90eller), hvor to har samme mål.
Komponenter (rediger)
- Median: er en linje, der starter fra midtpunktet på den ene side og når det modsatte toppunkt. De tre medianer konvergerer på et punkt kaldet barycenter eller centroid..
- Bisector: er en stråle, der deler vinklen på hvert toppunkt i to lige store vinkler. Derfor er det kendt som symmetriaksen, og denne type trekanter har kun en.
- Mediatrixen: er et segment vinkelret på siden af trekanten, som har sin oprindelse i midten af trekanten. Der er tre lægemidler i en trekant, og de mødes på et punkt kaldet circumcenter.
- Højden: er linjen, der går fra toppunktet til den side, der er modsat, og også denne linje er vinkelret på den side. Alle trekanter har tre højder, som falder sammen på et punkt kaldet ortocentret..
Ejendomme
Ensartede trekanter defineres eller identificeres, fordi de har flere egenskaber, der repræsenterer dem, og som stammer fra sætninger, der er foreslået af store matematikere:
Indvendige vinkler
Summen af de indvendige vinkler er altid lig med 180eller.
Summen af siderne
Summen af målene fra to sider skal altid være større end målene for den tredje side, a + b> c.
Kongruente sider
Ensartede trekanter har to sider med samme mål eller længde; de er kongruente, og den tredje side er forskellig fra disse.
Kongruente vinkler
Isosceles trekanter er også kendt som isoangle trekanter, fordi de har to vinkler, der har samme mål (kongruent). Disse er placeret i bunden af trekanten, modsat siderne, der har samme længde.
På grund af dette blev sætningen genereret, der siger, at:
"Hvis en trekant har to kongruente sider, vil vinklerne overfor disse sider også være kongruente." Derfor, hvis en trekant er ligebenet, er vinklerne på dens baser kongruente.
Eksempel:
Den følgende figur viser en trekant ABC. Ved at trække sin halvering fra toppunktet for vinkel B til basen er trekanten opdelt i to lige store trekanter BDA og BDC:
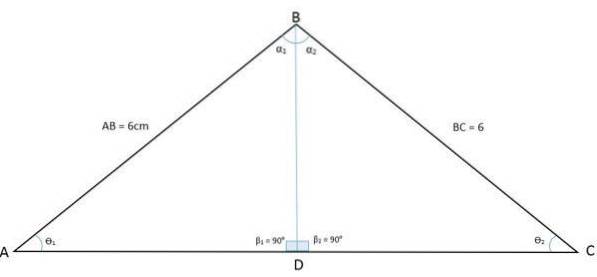
På denne måde blev vinklen på toppunkt B også delt i to lige store vinkler. Halveringen er nu den fælles side (BD) mellem disse to nye trekanter, mens siderne AB og BC er de kongruente sider. Således har vi tilfældet med kongruens side, vinkel, side (LAL).
Dette viser, at vinklerne på hjørnerne A og C har samme mål, såvel som det kan vises, at eftersom trekanterne BDA og BDC er kongruente, er siderne AD og DC også kongruente..
Højde, median, bisector og bisector er sammenfaldende
Linjen, der er trukket fra toppunktet modsat basen til midtpunktet for basen af den ligebenede trekant, er samtidig højden, medianen og halveringen, såvel som halveringen i forhold til den modsatte vinkel af basen..
Alle disse segmenter falder sammen i et, der repræsenterer dem.
Eksempel:
Den følgende figur viser trekanten ABC med et midtpunkt M, der deler basen i to segmenter BM og CM.
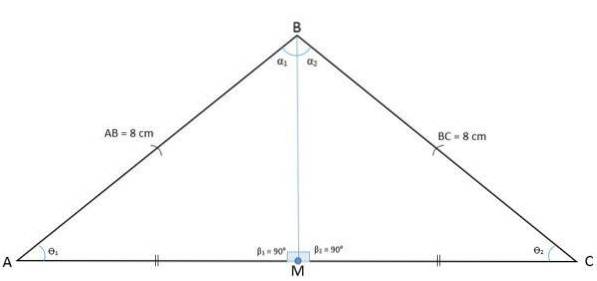
Ved at tegne et segment fra punkt M til det modsatte toppunkt opnås per definition medianen AM, som er relativ til toppunkt A og side BC.
Da segmentet AM opdeler trekanten ABC i to lige store trekanter AMB og AMC, betyder det, at tilfældet med kongruensside, vinkel, side vil blive haft, og derfor vil AM også være halveringspunktet for BC.
Derfor er halveringen altid lig medianen og omvendt..
Segmentet AM danner vinkler, der har samme mål for trekanterne AMB og AMC; de er supplerende på en sådan måde, at målene for hver enkelt vil være:
Med. (AMB) + Med. (AMC) = 180eller
to * Med. (AMC) = 180eller
Med. (AMC) = 180eller ÷ 2
Med. (AMC) = 90eller
Det kan være kendt, at vinklerne dannet af segment AM i forhold til bunden af trekanten er rigtige, hvilket indikerer, at dette segment er helt vinkelret på basen..
Repræsenterer derfor højden og halveringen, vel vidende at M er midtpunktet.
Derfor linjen AM:
- Repræsenterer i højden af f.Kr..
- Er mellemstor.
- Det er indeholdt i halveringen af BC.
- Det er halveringspunktet i toppunktvinklen Â
Relative højder
Højder, der er relative til lige sider, har også den samme måling.
Da den ligebenede trekant har to lige store sider, vil deres to respektive højder også være ens..
Ortocenter, barycenter, incenter og sammenfaldende circumcenter
Da højden, medianen, bisektoren og bisektoren i forhold til basen, er repræsenteret på samme tid af det samme segment, vil orthocentret, centerbarycenteret og circumcenteret være kollinære punkter, det vil sige de vil være på samme linje:

Sådan beregnes omkredsen?
Omkredsen af en polygon beregnes ved at tilføje siderne.
Som i dette tilfælde har den ligebenede trekant to sider med samme mål, dens omkreds beregnes med følgende formel:
P = 2*(side a) + (side b).
Sådan beregnes højden?
Højden er linjen vinkelret på basen, den deler trekanten i to lige store dele, når den strækker sig til det modsatte toppunkt.
Højden repræsenterer det modsatte ben (a), midten af basen (b / 2) det tilstødende ben og siden "a" repræsenterer hypotenusen.
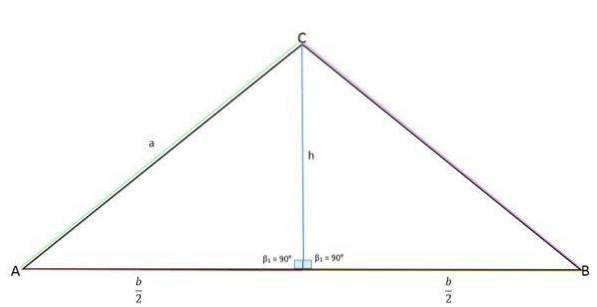
Ved hjælp af Pythagoras sætning kan værdien af højden bestemmes:
tilto + bto = cto
Hvor:
tilto = højde (h).
bto = b / 2.
cto = side a.
Ved at erstatte disse værdier i Pythagoras sætning og løse højden har vi:
hto + (b / to)to = tilto
hto + bto / 4 = tilto
hto = tilto - bto / 4
h = √ (tilto - bto / 4).
Hvis vinklen dannet af de kongruente sider er kendt, kan højden beregnes med følgende formel:

Sådan beregnes arealet?
Arealet af trekanterne beregnes altid med den samme formel, gangende basis gange højden og divideres med to:

Der er tilfælde, hvor kun målingerne af to sider af trekanten og vinklen dannet mellem dem er kendt. I dette tilfælde er det nødvendigt at anvende de trigonometriske forhold for at bestemme området:
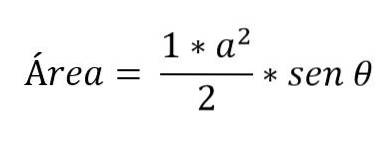
Sådan beregnes bunden af trekanten?
Da den ligebenede trekant har to lige store sider, er det nødvendigt at kende i det mindste mål for højden eller en af dens vinkler for at bestemme værdien af dens base.
At kende højden bruges den Pythagoras sætning:
tilto + bto = cto
Hvor:
tilto = højde (h).
cto = side a.
bto = b / 2, er ukendt.
Vi løser for bto af formlen, og vi skal:
bto = ato - cto
b = √ ato - cto
Da denne værdi svarer til halvdelen af basen, skal den ganges med to for at opnå det komplette mål for bunden af den ligebenede trekant:
b = 2 * (√ ato - cto)
I tilfælde af at kun værdien af dens lige sider og vinklen mellem dem er kendt, anvendes trigonometri, der tegner en linje fra toppunktet til basen, der deler den ligebenede trekant i to højre trekanter.
På denne måde beregnes halvdelen af basen med:

Det er også muligt, at kun værdien af toppunktets højde og vinkel, der er overfor basen, er kendt. I så fald ved hjælp af trigonometri kan basen bestemmes:

Uddannelse
Første øvelse
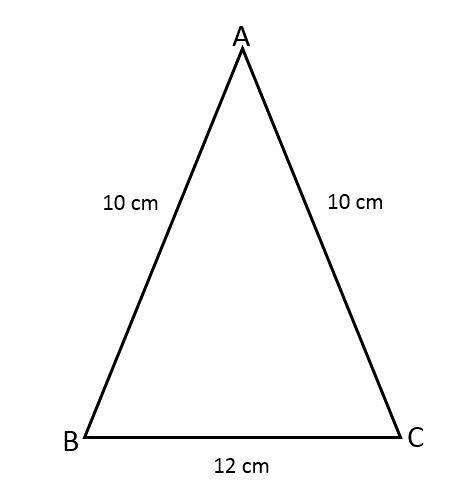
Find arealet af den ligebenede trekant ABC, idet du ved, at to af dens sider er 10 cm og den tredje side er 12 cm.
Opløsning
For at finde arealet af trekanten er det nødvendigt at beregne højden ved hjælp af områdeformlen, der er relateret til Pythagoras sætning, da værdien af vinklen dannet mellem de lige sider ikke er kendt.
Vi har følgende data om den ligebenede trekant:
- Lige sider (a) = 10 cm.
- Bund (b) = 12 cm.
Værdierne er substitueret i formlen:

Anden øvelse
Længden af de to lige sider af en ligebenet trekant er 42 cm, foreningen af disse sider danner en vinkel på 130eller. Bestem værdien af den tredje side, området for den trekant og omkredsen.
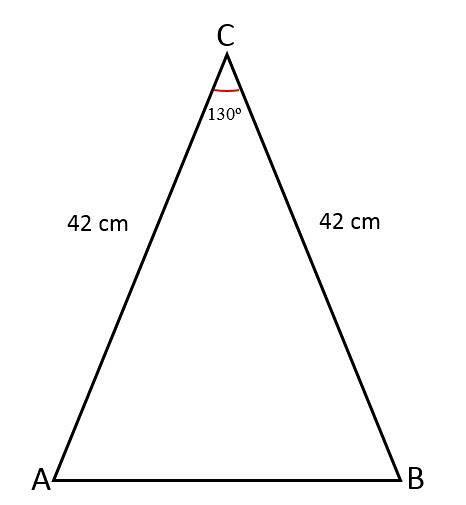
Opløsning
I dette tilfælde er målingerne af siderne og vinklen mellem dem kendt..
For at kende værdien af den manglende side, det vil sige bunden af den trekant, tegnes en linje vinkelret på den, der deler vinklen i to lige store dele, en for hver højre trekant, der dannes.
- Lige sider (a) = 42 cm.
- Vinkel (Ɵ) = 130eller
Nu ved trigonometri beregnes værdien af halvdelen af basen, hvilket svarer til halvdelen af hypotenusen:
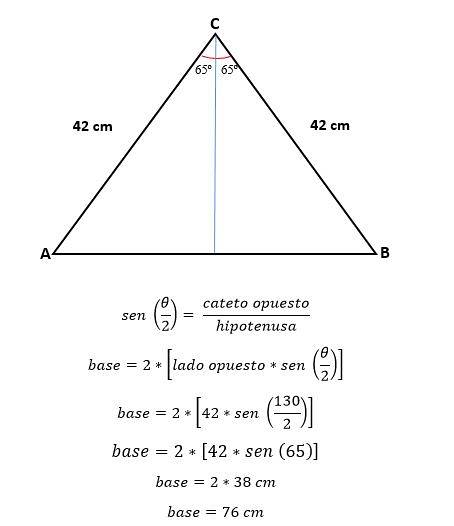
For at beregne arealet er det nødvendigt at kende højden af den trekant, der kan beregnes ved hjælp af trigonometri eller af den pythagoriske sætning, nu hvor basisværdien allerede er bestemt.
Ved trigonometri vil det være:

Omkredsen beregnes:
P = 2*(side a) + (side b).
P = 2* (42 cm) + (76 cm)
P = 84 cm + 76 cm
P = 160 cm.
Tredje øvelse
Beregn de indre vinkler af den ligebenede trekant, idet du ved, at vinklen på basen er  = 55eller
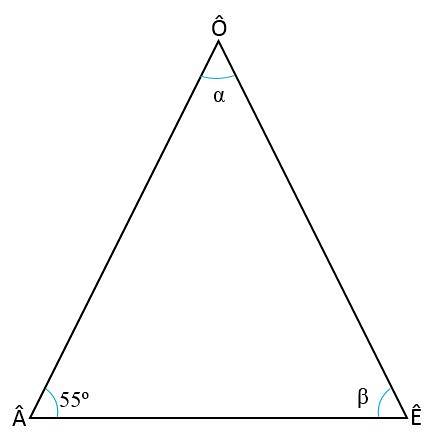
Opløsning
For at finde de to manglende vinkler (Ê og Ô) er det nødvendigt at huske to egenskaber af trekanter:
- Summen af de indvendige vinkler i hver trekant vil altid være = 180eller:
 + Ê + Ô = 180 eller
- I en ligebenet trekant er vinklerne på basen altid kongruente, dvs. de har samme mål, derfor:
 = Ô
Ê = 55eller
For at bestemme værdien af vinklen Ê erstatter vi værdierne for de andre vinkler i den første regel og løser for Ê:
55eller + 55eller + Ô = 180 eller
110 eller + Ô = 180 eller
Ô = 180 eller - 110 eller
Ô = 70 eller.
Referencer
- Álvarez, E. (2003). Elementer af geometri: med adskillige øvelser og kompasets geometri. University of Medellin.
- Álvaro Rendón, A. R. (2004). Teknisk tegning: aktivitetsbog.
- Angel, A. R. (2007). Elementær algebra. Pearson Uddannelse.
- Arthur Goodman, L. H. (1996). Algebra og trigonometri med analytisk geometri. Pearson Uddannelse.
- Baldor, A. (1941). Algebra. Havana: Kultur.
- José Jiménez, L. J. (2006). Matematik 2.
- Tuma, J. (1998). Ingeniørmatematikhåndbog. Wolfram MathWorld.



Endnu ingen kommentarer