
Oval (geometrisk figur) egenskaber, eksempler, øvelser
Det oval symmetrisk er defineret som en flad og lukket kurve, som har to vinkelrette symmetriakser-en dur og en mindre- og består af to omkredsbuer lige to og to.
På denne måde kan det tegnes ved hjælp af et kompas og nogle referencepunkter på en af symmetriens linjer. Under alle omstændigheder er der flere måder at tegne det på, som vi vil se senere.

Det er en meget velkendt kurve, da den genkendes som konturen af en ellipse, dette er et særligt tilfælde af den ovale. Men den ovale er ikke en ellipse, selvom den undertiden ligner den meget, da dens egenskaber og layout er forskellige. For eksempel er ellipsen ikke konstrueret med et kompas.
Artikelindeks
- 1 Funktioner
- 2 Eksempler
- 2.1 Konstruktion af en oval ved hjælp af koncentriske cirkler
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referencer
Egenskaber
Den ovale har meget varierede anvendelser: arkitektur, industri, grafisk design, urmageri og smykker er blot nogle områder, hvor dens anvendelse skiller sig ud..
De mest fremragende egenskaber ved denne vigtige kurve er følgende:
-Det hører til gruppen af tekniske kurver: det tegnes ved at danne perifere buer ved hjælp af et kompas.
-Alle dens punkter er på samme plan.
-Mangler kurver eller løkker.
-Dens layout er kontinuerligt.
-Den ovale kurve skal være glat og konveks.
-Når du tegner en linje, der tangerer det ovale, er det hele på den samme side af linjen.
-En oval tillader kun højst to tangenter parallelle.
Eksempler
Der er flere metoder til at konstruere ovaler, der kræver brug af en lineal, firkant og kompas. Så skal vi nævne nogle af de mest anvendte.
Konstruktion af en oval ved hjælp af koncentriske cirkler
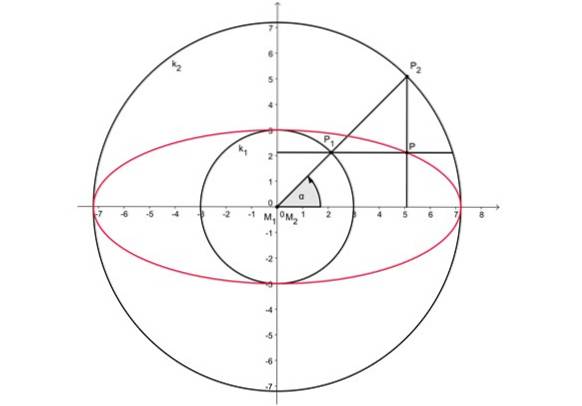
Figur 2 ovenfor viser to koncentriske cirkler centreret ved oprindelsen. Ovalens hovedakse måler det samme som diameteren på den ydre omkreds, mens den mindre akse svarer til diameteren på den indre omkreds.
-En vilkårlig radius trækkes mod den ydre omkreds, som skærer begge cirkler ved punkterne P1 Og sto.
-Derefter projiceres punkt Pto på den vandrette akse.
-På samme måde projiceres punktet P1 på den lodrette akse.
-Skæringspunktet mellem begge projektionslinjer er punkt P og hører til det ovale.
-Alle punkterne i dette afsnit af den ovale kan afbildes på denne måde.
-Resten af det ovale spores med den analoge procedure, der udføres i hver kvadrant.
Uddannelse
Dernæst vil andre måder at konstruere ovaler undersøges på, givet en bestemt indledende måling, der bestemmer deres størrelse..
- Øvelse 1
Tegn ved hjælp af en lineal og et kompas en oval, kendt som dens hovedakse, hvis længde er 9 cm.
Opløsning
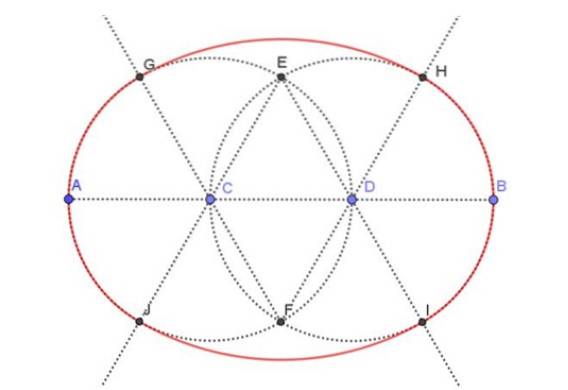
I figur 3, vist nedenfor, vises den resulterende ovale i rødt. Der skal lægges særlig vægt på de stiplede linjer, som er de hjælpekonstruktioner, der er nødvendige for at tegne en oval, hvis hovedakse er specificeret. Vi vil angive alle de nødvendige trin for at nå den endelige tegning.
Trin 1
Tegn med lineal segmentet AB på 9 cm.
Trin 2
Trisect segment AB, det vil sige opdele det i tre segmenter af samme længde. Da det originale segment AB er 9 cm, skal segmenterne AC, CD og DB hver måle 3 cm.
Trin 3
Med kompasset, centreret ved C og åbning CA, trækkes en hjælpeomkreds. Tilsvarende er den ekstra omkreds med centrum D og radius DB tegnet med kompasset..
Trin 4
Skæringspunkterne for de to hjælpecirkler, der blev bygget i det foregående trin, er markeret. Vi kalder det punkter E og F.
Trin 5
Med reglen tegnes følgende stråler: [FC), [FD), [EC], [ED).
Trin 6
Strålerne fra det foregående trin skærer de to hjælpecirkler ved henholdsvis punkterne G, H, I, J.
Trin 7
Med kompasset er centret lavet i F, og med åbning (eller radius) FG tegnes buen GH. På samme måde er buen trukket centreret ved E og radius EI IJ.
Trin 8
Foreningen af buerne GJ, JI, IH Y HG danner en oval, hvis hovedakse er 9 cm.
Trin 9
Vi fortsætter med at slette (skjule) hjælpepunkter og linjer.
- Øvelse 2
Tegn en oval med lineal og kompas, hvis mindre akse er kendt og dens mål er 6 cm.
Opløsning
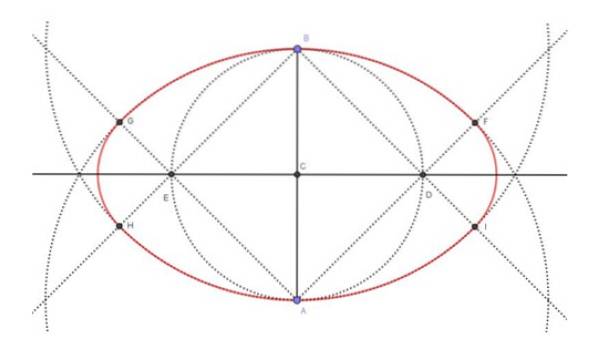
Figuren ovenfor (figur 4) viser det endelige resultat af konstruktionen af den ovale (i rødt) samt de mellemliggende konstruktioner, der er nødvendige for at nå den. De trin, der blev fulgt for at opbygge den 6 cm mindre akse ovale, var som følger:
Trin 1
Det 6 cm lange segment AB spores med linealen.
Trin 2
Med kompasset og linealen spores halveringslinjen til segment AB.
Trin 3
Skæringspunktet mellem bisektoren og segmentet AB resulterer i midtpunktet C for segmentet AB.
Trin 4
Med kompasset tegnes omkredsen af centrum C og radius CA.
Trin 5
Omkredsen, der er tegnet i det foregående trin, skærer tværsnittet af AB ved punkterne E og D..
Trin 6
Strålerne [AD], [AE), [BD) og [BE) er tegnet.
Trin 7
Med kompasset tegnes omkredsen af centrum A og radius AB og centrum B og radius BA..
Trin 8
Skæringspunkterne mellem cirklerne tegnet i trin 7 og strålerne konstrueret i trin 6 bestemmer fire punkter, nemlig: F, G, H, I.
Trin 9
Med centrum ved D og radius DI tegnes lysbuen IF. På samme måde, med centrum i E og radius EG, tegnes lysbuen GH.
Trin 10
Foreningen af omkredsbuerne FG, GH, HI og IF bestemmer den ønskede ovale.
Referencer
- Ed Plastic. Tekniske kurver: ovale, ovale og spiraler. Gendannet fra: drajonavarres.wordpress.com.
- Mathematische Basteleien. Ægkurver og ovaler. Gendannet fra: mathematische-basteleien.
- Universitetet i Valencia. Konik og flade tekniske kurver. Gendannet fra: ocw.uv.es.
- Wikipedia. Oval. Gendannet fra: es.wikipedia.org.
- Wikipedia. Oval. Gendannet fra: en.wikipedia.org.



Endnu ingen kommentarer