Lineært variationskoncept, eksempler, løst øvelse

Det lineær variation opstår mellem to fysiske størrelser, når grafen, der repræsenterer dem, er en lige linje. Det svarer til at bekræfte, at variablerne er i lineær afhængighed på en sådan måde, at hvis vi kalder en af ​​dem "y" og den anden "x", vil de være relateret ved hjælp af det matematiske udtryk:

y = mx + b

I denne formel er m og b reelle tal. Værdien af ​​m repræsenterer liniens hældning eller hældning - som altid er konstant - og b er linjens snit med den lodrette akse.

Hvert fænomen, der reagerer på en lineær variation, har forskellige navne på variablerne, som vi vil se i de følgende eksempler. Den matematiske form for ligningen er dog den samme.

Eksperimentelt kan det fastslås, om der er en lineær sammenhæng mellem to størrelser, der måler par af værdier (x, y).

De således opnåede punkter er plottet på grafpapir, og det observeres, hvis de har en lineær tendens, det vil sige, hvis der er en linje, der passer til de eksperimentelle data.

I første omgang kan denne linje trækkes visuelt, men ved hjælp af a lineær regression kan findes analytisk, værdierne for m og b for den linje, der bedst passer til de eksperimentelle punkter.

Artikelindeks

• 1 Eksempler på lineær variation
  • 1.1 Hastighed i retlinet bevægelse ensartet varieret
  • 1.2 Termisk ekspansion
  • 1.3 Placering af en mobil med konstant hastighed
  • 1.4 En persons højde
  • 1.5 Temperaturskalaer
  • 1.6 Tryk og dybde
• 2 Øvelse løst
  • 2.1 Kørselsomkostninger
• 3 Referencer

Eksempler på lineær variation

Der er adskillige naturlige fænomener samt sammenhænge mellem målestandarder, der skyldes lineær variation, for eksempel:

Hastighed i retlinet bevægelse varieret ensartet

Hastigheden som en funktion af tiden v (t) for en mobil, der bevæger sig langs en linje med konstant acceleration a og starthastighed v_eller  forskellig fra 0. Denne bevægelse er kendt som ensartet varieret retlinet bevægelse og ligningen for hastighed er:

v (t) = v_eller + på

Varmeudvidelse

Et andet naturligt fænomen, hvis variation er lineær, er den stigning i længde, som en stang eller ledning oplever, når den opvarmes..

Når temperaturen på et objekt stiger, øges dets dimensioner faktisk, og denne stigning afhænger af ændringen i temperaturen AT og en mængde kaldet koefficient for lineær ekspansion betegnet med det græske bogstav α:

L = L._eller + α ΔT

I dette udtryk er L den endelige længde af objektet og L_eller er dens oprindelige længde.

Placering af en mobil med konstant hastighed

En mobil med hastighed konstant bevæger sig altid i en lige linje. Hvis den lige linje er den vandrette x-akse, gives positionen x (t) til enhver tid af:

x (t) = x_eller + vt

Hvor x_eller er startpositionen, v er hastigheden, og t er tiden. På denne måde siges det, at positionen x varierer lineært med tiden t.

En persons højde

Læger og antropologer kan estimere en persons højde ved at måle lårbenets længde..

Jo højere en person er, jo længere er benene, så der er lineære modeller til at forudsige højden af ​​en voksen H (i inches), hvis længden L (også i inches) af hans lårben er kendt ifølge ligningen:

H = 1.880 ° L + 32.010

Temperaturskalaer

Celsius- og Fahrenheit-skalaen bruges dagligt til måling af temperaturer. Denne sidste skala bruges ofte i engelsktalende lande. Der er en ækvivalens at gå fra den ene til den anden:

F = (9/5) C + 32

Hvor F er temperaturen i grader Fahrenheit, og C er temperaturen i grader Celsius.

Tryk og dybde

Det absolutte tryk P i en ukomprimerbar væske såsom vand, hvis konstante tæthed er ρ, varierer som en funktion af dybde h som:

P = P_eller + ρgh

Hvor P_eller er trykket ved den frie overflade af væsken. Hvis væsken er i en beholder, der er åben for atmosfæren, er dette tryk simpelthen det atmosfæriske tryk P_pengeautomat, kunne skrive derefter:

P = P_pengeautomat + ρgh

Det atmosfæriske tryk ved havoverfladen er ca. 101 kPa. Dette forhold mellem P og h betyder, at trykket stiger lineært med dybden..

Træning løst

Kørselsomkostninger

De månedlige omkostninger C ved bilkørsel inkluderer en fast månedlig pris C_eller plus omkostningerne ved kilometertal eller kørt kilometer hver måned. En chauffør bemærker, at i en given måned var kørselsomkostningerne $ 380 for 480 miles, og den næste måned var det $ 460 for 800 miles.

Lad d være antallet af miles, som chaufføren har kørt om måneden med de leverede data, find:

a) Den lineære variation mellem C og d.

b) Hvor meget vil det koste pr. måned at køre bilen på en rejse på 1.500 kilometer?

c) Grafen for C versus d.

Løsning til

Antag, at variablerne har et forhold givet af:

C = C_eller + A.d

Hvor A og C_eller er konstanter, der skal bestemmes. A er hældningen på linjen, der grafisk repræsenterer forholdet mellem C og d. Co er snittet med den lodrette akse, den faste månedlige pris, som chaufføren skal betale for den kendsgerning, at han har bilen tilgængelig. Dette kan f.eks. Omfatte vedligeholdelsesomkostninger og skatter.

For utvetydigt at bestemme en linje er det nødvendigt at kende dens hældning. Til dette har vi punkterne:

P₁: 480 miles, $ 380

P_to: 800 miles, $ 460

Disse punkter af koordinater (d, C) eller (afstand, pris) er analoge med koordinaterne (x, y) for det kartesiske plan, hvilke ændringer er navnene. Linjens hældning A gives derefter ved:

A = (C_to - C₁) / (d_to - d₁)

A = [(460 - 380) $ / (800 - 480) miles] = (1/4) $ / mile

Linjens hældning repræsenterer prisen pr. Mil, sådan:

C = C_eller + A.d = Co + (1/4). D

For at bestemme omkostningerne ved base C_eller Denne ligning tages, og et af de punkter, som vi ved hører til, erstattes, for eksempel P₁:

380 $ = C_eller + [(1/4) $ / mile]. 480 mil → 380 $ = C_eller + $ 120

C_eller = $ 260

Nu kan vi formulere den lineære variantmodel som:

C = 260 + (1/4) d

Løsning b

De månedlige omkostninger ved at rejse 1500 miles er:

C = 260 + (1/4) x $ 1500 = $ 635

Løsning c

Grafen for C versus d er:

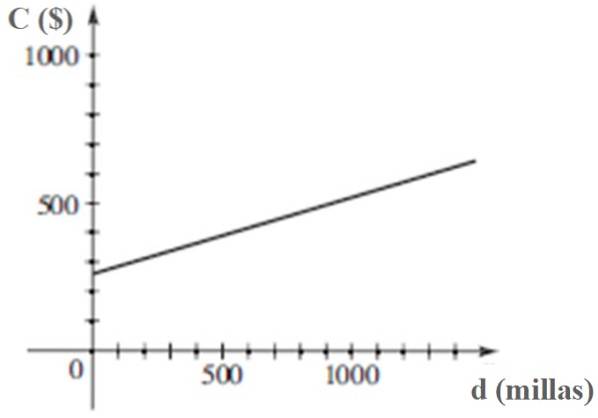
Referencer

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturudgaver.
2. Hoekenga, C. Lineære ligninger i videnskab. Gendannet fra: visionlearning.com.
3. Hoffman, J. Selection of Mathematics Topics. Bind 2.
4. Jiménez, R. 2008. Algebra. Prentice hall.
5. Stewart, J. 2006. Precalculus: Matematik til beregning. 5. plads Udgave. Cengage læring.
6. Zill, D. 1984. Algebra og trigonometri. Mcgraw bakke.