Vektoregenskaber og egenskaber, elementer, typer, eksempler

Det vektor De er matematiske enheder, der har en -positiv-størrelse, generelt ledsaget af en måleenhed, samt retning og sans. Sådanne egenskaber er meget passende til at beskrive fysiske størrelser såsom hastighed, kraft, acceleration og mange flere..

Med vektorer er det muligt at udføre operationer såsom addition, subtraktion og produkter. Opdeling er ikke defineret for vektorer, og som for produktet er der tre klasser, som vi vil beskrive senere: prikprodukt eller punkt, vektorprodukt eller kryds og produkt af en skalar med en vektor.

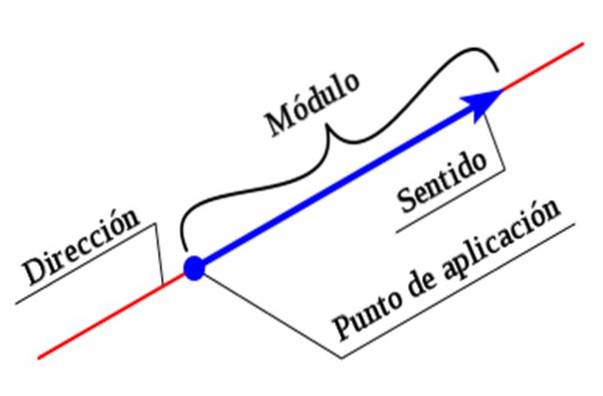
For fuldt ud at beskrive en vektor er det nødvendigt at angive alle dens egenskaber. Størrelsen eller modulet er en numerisk værdi ledsaget af en enhed, mens retning og retning etableres ved hjælp af et koordinatsystem.

Lad os se på et eksempel: Lad os sige, at et fly flyver fra en by til en anden med en hastighed på 850 km / t i retning NE. Her har vi en fuldt specificeret vektor, da størrelsen er tilgængelig: 850 km / t, mens retning og sans er NE.

Vektorer er normalt repræsenteret grafisk af orienterede linjesegmenter, hvis længde er proportional med størrelsen.

Mens man specificerer retningen og følelsen, kræves der en referencelinje, som normalt er den vandrette akse, selvom nord også kan tages som en reference, er dette tilfældet med planens hastighed:

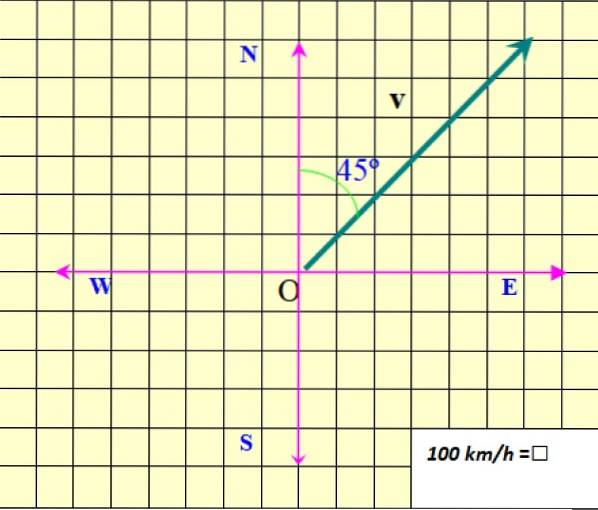
Figuren viser planetens hastighedsvektor, der betegnes som v på fremhævet, for at skelne den fra en skalar størrelse, som kun kræver en numerisk værdi og en eller anden enhed, der skal specificeres.

Artikelindeks

• 1 Elementer af en vektor
  • 1.1 Rektangulære komponenter i en vektor
• 2 slags
  • 2.1 Ortogonale enhedsvektorer
• 3 Summen af ​​vektorer
  • 3.1 Egenskaber ved vektortilsætning
• 4 vektoreksempler
• 5 Andre operationer mellem vektorer
  • 5.1 Produkt af en skalar og en vektor
  • 5.2 Skalarprodukt eller prikprodukt mellem vektorer
  • 5.3 Krydsprodukt eller krydsprodukt mellem vektorer
• 6 Løst øvelser
  • 6.1 - Øvelse 1
  • 6.2 - Øvelse 2
• 7 Referencer

Elementer af en vektor

Som vi har sagt, er elementerne i vektoren:

-Størrelse eller modul, undertiden også kaldet vektorens absolutte værdi eller norm.

-Retning

-Følelse

I eksemplet i figur 2 er modulet v Det er 850 km / t. Modulet betegnes som v uden fed skrift eller som |v|, hvor bjælkerne repræsenterer den absolutte værdi.

Adressen til v er specificeret med hensyn til Nord. I dette tilfælde er det 45 ° nord for øst (45 ° NØ). Endelig informerer spidsen af ​​pilen om retningen af v.

I dette eksempel er vektorens oprindelse tegnet sammenfaldende med oprindelsen O for koordinatsystemet, dette er kendt som bundet vektor. På den anden side, hvis oprindelsen af ​​vektoren ikke falder sammen med referencesystemets, siges det at være en gratis vektor.

Det skal bemærkes, at for at specificere vektoren fuldt ud, skal disse tre elementer bemærkes, ellers ville beskrivelsen af ​​vektoren være ufuldstændig.

Rektangulære komponenter i en vektor

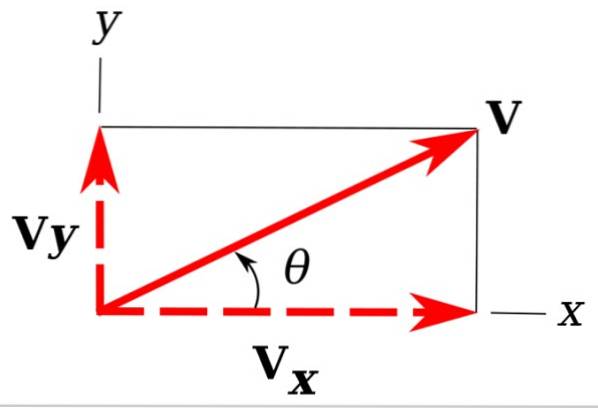
På billedet har vi vores eksempelvektor tilbage v, der er i flyet xy.

Det er let at se, at fremspringene på v på x- og y-koordinatakserne bestemmer en ret trekant. Disse fremskrivninger er v_Y Y v_x og kaldes rektangulære komponenter af v.

En måde at betegne v gennem dens rektangulære komponenter er sådan: v = x, v_Y>. Disse parenteser bruges i stedet for parenteser for at understrege, at det er en vektor og ikke et punkt, da i dette tilfælde parenteser ville blive brugt.

Hvis vektoren er i et tredimensionelt rum, er der brug for endnu en komponent, så:

v = x, v_Y, v_z>

At kende de rektangulære komponenter, beregnes vektorens størrelse, svarende til at finde hypotenusen i den højre trekant, hvis ben er v_x Y v_Y,. Ved hjælp af Pythagoras sætning følger det, at:

|v|^to = (v_x)^to +  (v_Y)^to

Polær form af en vektor

Når vektorens størrelse er kendt |v| og vinklen θ, som dette dannes med referenceaksen, generelt den vandrette akse, er vektoren også specificeret. Vektoren siges derefter at være udtrykt i polær form.

De rektangulære komponenter i dette tilfælde beregnes let:

v_x = |v| .cos θ

v_Y = |v| .sen θ

Ifølge ovenstående er de rektangulære komponenter i hastighedsvektoren v af flyet ville være:

v_x = 850. cos 45º km / t = 601,04 km / t

v_Y = 850. sin 45º km / t = 601,04 km / t

Typer

Der er flere typer vektorer. Der er vektorer med hastighed, position, forskydning, kraft, elektrisk felt, momentum og mange flere. Som vi allerede har sagt, er der i fysikken et stort antal vektormængder.

Hvad angår vektorer, der har visse egenskaber, kan vi nævne følgende typer af vektorer:

-Nul: dette er vektorer, hvis størrelse er 0, og som betegnes som 0. Husk, at det fede bogstav symboliserer de tre grundlæggende egenskaber ved en vektor, mens det normale bogstav kun repræsenterer modulet.

For eksempel på et legeme i statisk ligevægt skal summen af ​​kræfter være en nulvektor.

-Gratis og bundet: gratis vektorer er dem, hvis oprindelses- og ankomstpunkter er et par punkter i flyet eller i rummet, i modsætning til sammenkædede vektorer, hvis oprindelse falder sammen med det i det referencesystem, der bruges til at beskrive dem.

Parret eller øjeblikket produceret af et par kræfter er et godt eksempel på en fri vektor, da parret ikke gælder for noget bestemt punkt.

-Teamlinser: de er to gratis vektorer, der har identiske egenskaber. Derfor har de samme størrelse, retning og sans.

-Coplanar eller coplanar: vektorer, der hører til det samme plan.

-Modsætninger: vektorer med samme størrelse og retning, men modsatte retninger. Vektoren overfor en vektor v er vektoren -v og summen af ​​begge er nulvektoren: v + (-v) = 0.

-Samtidig: vektorer, hvis handlingslinjer alle passerer gennem det samme punkt.

-Glidere: er de vektorer, hvis applikationspunkt kan glide langs en bestemt linje.

-Collinear: vektorer, der er placeret på samme linje.

-Enhed: de vektorer, hvis modul er 1.

Ortogonale enhedsvektorer

Der er en meget nyttig type vektor i fysik kaldet en ortogonal enhedsvektor. Den ortogonale enhedsvektor har et modul svarende til 1, og enhederne kan være hvilke som helst, for eksempel dem med hastighed, position, kraft eller andre.

Der er et sæt specielle vektorer, der hjælper med let at repræsentere andre vektorer og udføre operationer på dem: de er ortogonale enhedsvektorer jeg, j Y k, enhed og vinkelret på hinanden.

I to dimensioner er disse vektorer rettet langs den positive retning af begge akser x fra aksen Y. Og i tre dimensioner tilføjes en enhedsvektor i retning af aksen z positiv. De er repræsenteret som følger:

jeg = <1, 0,0>

j = < 0,1,0>

k = <0,0,1>

En vektor kan repræsenteres af enhedsvektorerne jeg, j Y k som følger:

v = v_x jeg + v_Y j + v_z k

For eksempel hastighedsvektoren v fra ovenstående eksempler kan skrives som:

v = 601,04 jeg + 601.04 j km / t

Komponenten i k er ikke nødvendigt, da denne vektor er i planet.

Vector tilføjelse

Summen af ​​vektorer vises meget ofte i forskellige situationer, for eksempel når du vil finde den resulterende kraft på et objekt, der er påvirket af forskellige kræfter. Lad os begynde med at antage, at vi har to gratis vektorer eller Y v på flyet, som vist i følgende figur til venstre:

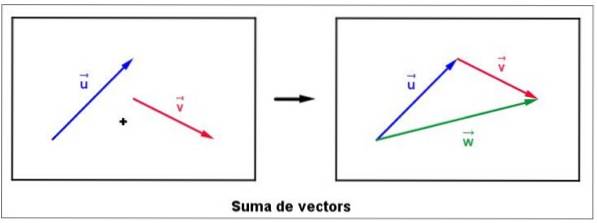
Det flyttes straks omhyggeligt til vektoren v, uden at ændre dens størrelse, retning eller sans, så dens oprindelse falder sammen med slutningen af eller.

Somme vektor kaldes w og tegnes startende fra u slutter i v, ifølge den rigtige figur. Det er vigtigt at bemærke, at størrelsen af ​​vektoren w er ikke nødvendigvis summen af ​​størrelsen af v Y eller.

Hvis du tænker nøje over det, er den eneste gang, at størrelsen af ​​den resulterende vektor er summen af ​​størrelsen af ​​addenderne, når begge addends er i samme retning og har samme sans..

Og hvad sker der, hvis vektorerne ikke er gratis? Det er også meget let at tilføje dem. Måden at gøre det på er at tilføje komponent til komponent eller analytisk metode.

Lad os som et eksempel overveje vektorerne i den følgende figur. Den første ting er at udtrykke dem på en af ​​de tidligere forklarede kartesiske måder:

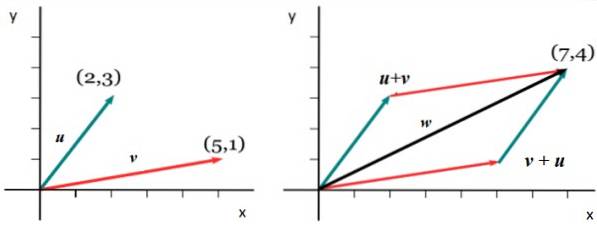
v = <5,1>

eller = <2,3>

For at få komponenten ind x af sumvektoren w, de respektive komponenter tilføjes i x fra v Y eller: w_x = 5 + 2 = 7. Og at få w_Y en analog procedure følges: w_Y = 1 + 3. Derfor:

eller = <7,4>

Egenskaber ved vektortilsætning

-Summen af ​​to eller flere vektorer resulterer i en anden vektor.

-Det er kommutativt, rækkefølgen af ​​tilføjelser ændrer ikke summen på en sådan måde, at:

eller + v = v + eller

-Det neutrale element i summen af ​​vektorer er nulvektoren: v + 0 = v

-Subtraktionen af ​​to vektorer er defineret som summen af ​​det modsatte: v - u = v + (-eller)

Vektoreksempler

Som vi har sagt, er der adskillige vektormængder i fysik. Blandt de bedst kendte er:

-Position

-Forskydning

-Gennemsnitlig hastighed og øjeblikkelig hastighed

-Acceleration

-Kraft

-Mængde af bevægelse

-Moment eller moment af en kraft

-Impuls

-elektrisk felt

-Magnetfelt

-Magnetisk øjeblik

På den anden side er de ikke vektorer, men skalarer:

-Vejr

-Masse

-Temperatur

-Bind

-Massefylde

-Mekanisk arbejde

-Energi

-Hed

-Strøm

-Spænding

-Elektrisk strøm

Andre operationer mellem vektorer

Ud over additionen og subtraktionen af ​​vektorer er der tre andre meget vigtige operationer mellem vektorerne, fordi de giver anledning til nye meget vigtige fysiske størrelser:

-Produkt af en skalar og en vektor.

-Prikproduktet eller prikproduktet mellem vektorer

-Og kors- eller vektorproduktet mellem to vektorer.

Produkt af en skalar og en vektor

Overvej Newtons anden lov, der siger, at styrken F og acceleration til de er proportionale. Proportionalitetskonstanten er massen m af objektet, derfor:

F = m.til

Masse er en skalar; kraft og acceleration er vektorer. Da kraften opnås ved at multiplicere massen med accelerationen, er det resultatet af produktet af en skalar og en vektor.

Denne type produkt resulterer altid i en vektor. Her er et andet eksempel: mængden af ​​bevægelse. Være P momentumvektoren, v hastighedsvektoren og som altid, m er massen:

P = m.v

Prikprodukt eller prikprodukt mellem vektorer

Vi har placeret mekanisk arbejde på listen over mængder, der ikke er vektorer. Arbejde i fysik er imidlertid resultatet af en operation mellem vektorer kaldet skalarprodukt, indre produkt eller prikprodukt..

Lad vektorerne være v Y eller, prikproduktet eller skalaren mellem dem er defineret som:

v∙eller = |v| ∙ |eller | .cos θ

Hvor θ er vinklen mellem de to. Fra den viste ligning følger det straks, at resultatet af punktproduktet er en skalar, og at hvis begge vektorer er vinkelrette, er deres skalære produkt 0.

Tilbage til mekanisk arbejde W, dette er det skalære produkt mellem kraftvektoren F og forskydningsvektoren ℓ.

W = F∙ℓ                  

Når vektorer er tilgængelige med hensyn til deres komponenter, er punktproduktet også meget let at beregne. Ja v = x, v_Y, v_z > Y eller = x, eller_Y, eller_z >, prikproduktet mellem de to er:

v∙eller = v_x eller_x + v_Y eller_Y + v_z eller_z

Prikproduktet mellem vektorer er kommutativt, derfor:

v∙eller = eller∙v

Kryds produkt eller vektorprodukt mellem vektorer

Ja v og u er vores to eksempelvektorer, vektorproduktet er defineret som:

v x eller = w

Det følger straks, at krydsproduktet resulterer i en vektor, hvis modul er defineret som:

|v x u | = | v | . | u |. sen θ

Hvor θ er vinklen mellem vektorerne.

Krydsproduktet er derfor ikke kommutativt v x u ≠ u x v. Faktisk v x u = - (u x v).

Hvis de to eksempler på vektorer udtrykkes i form af enhedsvektorerne, er beregningen af ​​vektorproduktet lettere:

v = v_x jeg + v_Y j + v_z k

eller = u_x jeg + eller_Y j + eller_z k

Kryds produkter mellem enhedsvektorer

Tværproduktet mellem identiske enhedsvektorer er nul, da vinklen mellem dem er 0º. Men mellem forskellige enhedsvektorer er vinklen mellem dem 90º og sin 90º = 1.

Følgende diagram hjælper med at finde disse produkter. I pilens retning har den en positiv retning og i den modsatte retning har den en negativ retning:

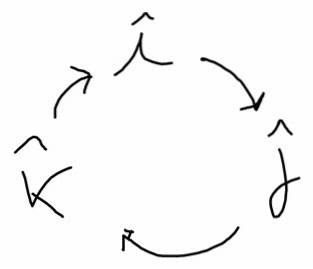
jeg x j = k, j x k = jeg; k x jeg = j; j x i = -k; k x j = -jeg; jeg x k = -j

Anvendelse af den distribuerende ejendom, som stadig er gyldig for produkterne mellem vektorer plus egenskaberne for enhedsvektorer, har vi:

v x eller = (v_x jeg + v_Y j + v_z k) x (u_x jeg + eller_Y j + eller_z k) =  

= (v_Yeller_z - v_zeller_Y )jeg + (v_zeller_x - v_xeller_z )j + (v_xeller_Y - v_Yeller_x )k

Løst øvelser

- Øvelse 1

Givet vektorerne:

v = -5 jeg + 4j + 1 k

eller = 2 jeg -3 j + 7k

Hvad skal være vektoren w så summen v + eller + w det viser sig 6 jeg +8 j -10k?

Opløsning

-5 jeg + 4j + 1 k

to jeg -3 j + 7k

 w_x jeg + w_Y j + w_z k  +

--

6jeg + 8 j -10 k

Derfor skal det være opfyldt, at:

-5 +2 + w_x = 6 → w_x = 9

4-3 + w_Y = 8 → w_Y = 7

1 + 7 + w_z = -10 → w_z = -18

Svaret er: w = 9 jeg +7 j - 18k

- Øvelse 2

Hvad er vinklen mellem vektorerne v Y eller fra øvelse 1?

Opløsning

Vi bruger prikproduktet. Fra definitionen har vi:

cos θ = v∙eller / |v| ∙ |eller|

v∙eller= -10 -12 + 7 = -15

|v| = √ (-5)^to +4^to +1^to= √42 = 6,48

|eller| = √2^to +(-3)^to +7^to= √62 = 7,87

Udskiftning af disse værdier:

cos θ = -15 / 6,48 x 7,87 = -0,2941 → θ = 107,1 º

Referencer

1. Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB).
2. Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
3. Rex, A. 2011. Grundlæggende fysik. Pearson.
4. Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
5. Serway, R., Jewett, J. 2008. Fysik til videnskab og teknik. Bind 1. 7. Ed. Cengage Learning.