
Vektor dirigerende ligning af linjen, løste øvelser
Det forstås af direktør vektor en, der definerer retningen af en linje, enten i planet eller i rummet. Derfor kan en vektor parallelt med linjen betragtes som en retningsvektor af den samme.
Dette er muligt takket være et aksiom med euklidisk geometri, der siger, at to punkter definerer en linje. Derefter definerer det orienterede segment dannet af disse to punkter også en direktørvektor af linjen.
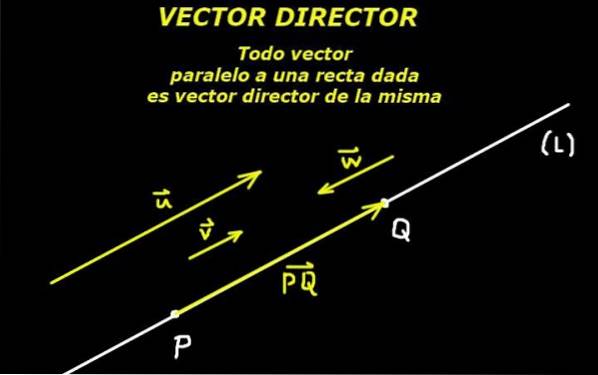
Givet et punkt P tilhører linjen (L) og givet en instruktørvektor eller af denne linje er linjen helt bestemt.
Artikelindeks
- 1 Ligning af linjen og direktørvektoren
- 1.1 Parametrisk ligning af linjen
- 2 Linjen i vektorform
- 2.1 Eksempel 2
- 2.2 Kontinuerlig form for linjen og instruktørvektoren
- 3 Generel form for linjens ligning
- 3.1 Eksempel 3
- 4 Standardform for linjens ligning
- 4.1 Eksempel 4
- 5 Øvelser løst
- 5.1-Øvelse 1
- 5.2-Øvelse 2
- 6 Referencer
Ligning af linjen og direktørvektoren
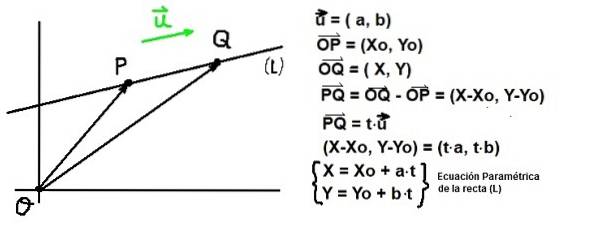
Givet et punkt P af koordinater Spørgsmål: (Xo, I) og en vektor eller direktør for en straight (L), alt pointer Spørgsmål af koordinater Spørgsmål: (X, Y) skal tilfredsstille, at vektoren PQ være parallel med u. Denne sidste betingelse er garanteret, hvis PQ er proportional med eller:
PQ = t⋅eller
i det forrige udtryk t er en parameter, der hører til de reelle tal.
Hvis de kartesiske komponenter i PQ og af eller Ovenstående ligning er skrevet som følger:
(X-Xo, Y-Yo) = t⋅ (a, b)
Hvis komponenterne i vektorligestilling udlignes, har vi følgende par ligninger:
X - Xo = a⋅t Y Y - I = b⋅t
Parametrisk ligning af linjen
Koordinaterne x og Y af et punkt på linjen (L) passerer gennem et koordinatpunkt (Xo, I) og det er parallelt med direktør vektor eller= (a, b) bestemmes ved at tildele reelle værdier til den variable parameter t:
X = Xo + a⋅t; Y = I + b⋅t
Eksempel 1
For at illustrere betydningen af linjens parametriske ligning tager vi som retningsvektoren
eller = (a, b) = (2, -1)
og som et kendt punkt på linjen punktet
P = (Xo, I) = (1, 5).
Linjens parametriske ligning er:
X = 1 + 2⋅t; Y = 5 - 1 t; -∞
For at illustrere betydningen af denne ligning vises figur 3, hvor parameteren t ændres i værdi og punkt Spørgsmål af koordinater (X, Y) tage forskellige positioner på lige.
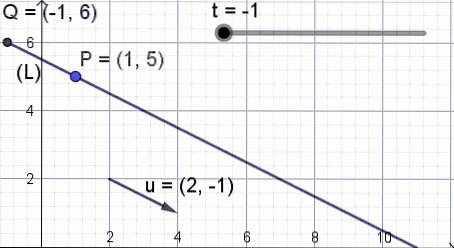
Linjen i vektorform
Givet et punkt P på linjen og dens direktørvektor u, kan linjens ligning skrives i vektorform:
OQ = OP + λ⋅eller
I ovenstående ligning er Q et hvilket som helst punkt, men hører til linjen og λ et reelt tal.
Linjens vektorligning gælder for ethvert antal dimensioner, selv en hyperlinie kan defineres.
I det tredimensionelle tilfælde for en instruktørvektor eller= (a, b, c) og et punkt P = (Xo, Yo, Zo), koordinaterne for et generisk punkt Q = (X, Y, Z) der hører til linjen er:
(X OG Z) = (Xo, Yo, Zo) + λ⋅ (a, b, c)
Eksempel 2
Overvej igen linjen, der har som en retningsvektor
eller = (a, b) = (2, -1)
og som et kendt punkt på linjen punktet
P = (Xo, I) = (1, 5).
Vektorligningen for denne linje er:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Kontinuerlig form for linjen og instruktørvektoren
Startende fra den parametriske form, rydning og ligning af parameteren λ, har vi:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
Dette er den symmetriske form af linjens ligning. jeg føler at til, b Y c er komponenterne i instruktørvektoren.
Eksempel 3
Overvej linjen, der har som en retningsvektor
eller = (a, b) = (2, -1)
og som et kendt punkt på linjen punktet
P = (Xo, I) = (1, 5). Find dens symmetriske form.
Linjens symmetriske eller kontinuerlige form er:
(X - 1) / 2 = (Y - 5) / (- 1)
Generel form for linjens ligning
Ligningen, der har følgende struktur, er kendt som den generelle form for linjen i XY-planet:
A⋅X + B⋅Y = C
Udtrykket for den symmetriske form kan omskrives til at have den generelle form:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
sammenlignet med linjens generelle form er det:
A = b, B = -a og C = b⋅Xo - a⋅Yo
Eksempel 3
Find den generelle form for linjen, hvis direktørvektor er u = (2, -1)
og der passerer gennem punktet P = (1, 5).
For at finde den generelle form kan vi bruge de givne formler, men der vælges en alternativ sti.
Vi starter med at finde den dobbelte vektor w af direktørvektoren u, defineret som den vektor, der opnås ved at udveksle komponenterne i u og gang den anden med -1:
w= (-1, -2)
den dobbelte vektor w svarer til en 90 ° rotation med uret af direktørvektoren v.
Vi formere os skalært w med (X, Y) og med (Xo, I) og vi matcher:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2-5 = -11
forbliver endelig:
X + 2Y = 11
Standardform for linjens ligning
Det er kendt som standardformen for linjen i XY-planet, en der har følgende struktur:
Y = m⋅X + d
hvor m repræsenterer hældningen og d skæringen med Y-aksen.
Givet retningsvektoren u = (a, b) er hældningen m b / a.
Yd opnås ved at erstatte X og Y med det kendte punkt Xo, I:
I = (b / a) Xo + d.
Kort sagt, m = b / a og d = I - (b / a) Xo
Bemærk, at hældningen m er kvotienten mellem komponenten Y af instruktørvektoren og komponenten x af det samme.
Eksempel 4
Find standardformen for linjen, hvis direktørvektor er u = (2, -1)
og der passerer gennem punktet P = (1, 5).
m = -½ og d = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Løst øvelser
-Øvelse 1
Find en direktørvektor for linjen (L), der er krydset mellem planet (Π): X - Y + Z = 3 og planet (Ω): 2X + Y = 1.
Skriv derefter den kontinuerlige form for ligningens linje (L).
Opløsning
Fra ligningen af planet (Ω) frigør Y: Y = 1-2X
Derefter erstatter vi i ligningen af planet (Π):
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Derefter parametriseres X, vælger vi parametriseringen X = λ
Dette betyder, at linjen har en vektorligning givet af:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
som kan omskrives som:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
med hvilket det er klart, at vektoren eller = (1, -2, -3) er en retningsvektor for linjen (L).
Den kontinuerlige form for linjen (L) er:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Øvelse 2
Givet 5X-planet + til Y + 4Z = 5
og linien, hvis ligning er X / 1 = (Y-2) / 3 = (Z -2) / (- 2)
Bestem værdien af til således at planet og linjen er parallelle.
Løsning 2
Vektoren n = (5, a, 4) er en vektor, der er normal i forhold til planet.
Vektoren eller = (1, 3, -2) er en direktørvektor for linjen.
Hvis linjen er parallel med planet, så n • v = 0.
(5, til, 4)•(1, 3, -2) = 5 +3til -8 = 0 ⇒ til= 1.
Referencer
- Fleming, W., & Varberg, D. E. (1989). Præcalculus matematik. Prentice Hall PTR.
- Kolman, B. (2006). Lineær algebra. Pearson Uddannelse.
- Leal, J. M., & Viloria, N. G. (2005). Flyanalytisk geometri. Mérida - Venezuela: Redaktionel Venezolana C. A.
- Navarro, Rocio. Vektorer. Gendannet fra: books.google.co.ve.
- Pérez, C. D. (2006). Forberegning. Pearson Uddannelse.
- Prenowitz, W. 2012. Grundlæggende begreber i geometri. Rowman & Littlefield.
- Sullivan, M. (1997). Forberegning. Pearson Uddannelse.

Endnu ingen kommentarer