
Resulterende vektorberegning, eksempler, øvelser
Det resulterende vektor er den, der opnås ved hjælp af en operation med vektorer, hvis resultat også er en vektor. Normalt er denne operation summen af to eller flere vektorer, ved hjælp af hvilke en vektor opnås, hvis virkning er ækvivalent.
På denne måde opnås vektorer såsom den resulterende hastighed, acceleration eller kraft. For eksempel når flere kræfter virker på et legeme F1, Fto, F3,…. vektorsummen af alle disse kræfter er ækvivalent med nettokraften (den resulterende), som matematisk udtrykkes som følger:
F1 + Fto + F3 +… = FR eller FN

Den resulterende vektor, uanset om det er kræfter eller en hvilken som helst anden vektorstørrelse, findes ved at anvende reglerne for vektoraddition. Da vektorerne har retning og sans foruden den numeriske værdi, er det ikke nok at tilføje modulerne for at få den resulterende vektor.
Dette gælder kun i det tilfælde, hvor de involverede vektorer er i samme retning (se eksempler). Ellers er det nødvendigt at anvende vektorsummemetoder, som afhængigt af tilfældet kan være geometriske eller analytiske..
Artikelindeks
- 1 Eksempler
- 1.1 Geometriske metoder til at tilføje to vektorer
- 2 Øvelser
- 2.1-Øvelse 1
- 2.2 Øvelse 2
- 3 Referencer
Eksempler
De geometriske metoder til at finde den resulterende vektor er den polygonale metode og parallelogrammetoden.
Hvad angår analytiske metoder, er der komponentmetoden, hvormed vektoren, der er resultatet af ethvert vektor-system, kan findes, forudsat at vi har dens kartesiske komponenter..
Geometriske metoder til at tilføje to vektorer
Antag, at vektorerne eller Y v (Vi betegner dem med fed skrift for at skelne dem fra skalarer). I figur 2a) har vi dem placeret på flyet. I figur 2 b) er den overført til vektoren v på en sådan måde, at dens oprindelse falder sammen med slutningen af eller. Den resulterende vektor går fra oprindelsen til den første (eller) til spidsen af den sidste (v):
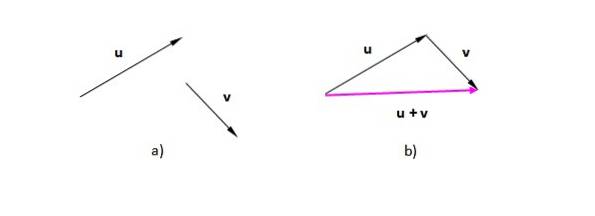
Den resulterende figur i dette tilfælde er en trekant (en trekant er en 3-sidet polygon). Hvis vi har to vektorer i samme retning, er proceduren den samme: placer den ene af vektorerne efter den anden og tegn en, der går fra oprindelsen eller halen til den første til spidsen eller enden af den sidste.
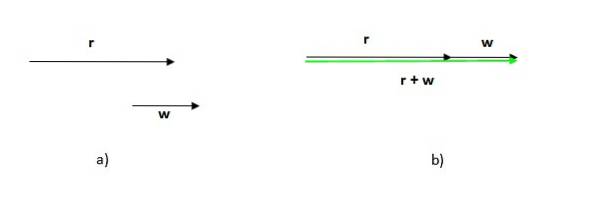
Bemærk, at rækkefølgen, i hvilken denne procedure udføres, ikke betyder noget, da summen af vektorer er kommutativ.
Bemærk også, at i dette tilfælde modul (længden eller størrelsen) af den resulterende vektor er summen af modulerne for de tilføjede vektorer, i modsætning til det foregående tilfælde, hvor modulet for den resulterende vektor er mindre end summen af modulerne for deltagerne.
Parallelogram metode
Denne metode er meget passende, når du skal tilføje to vektorer, hvis oprindelsespunkter falder sammen, f.eks. Med oprindelsen til et x-y-koordinatsystem. Antag, at dette er tilfældet for vores vektorer eller Y v (figur 3a):
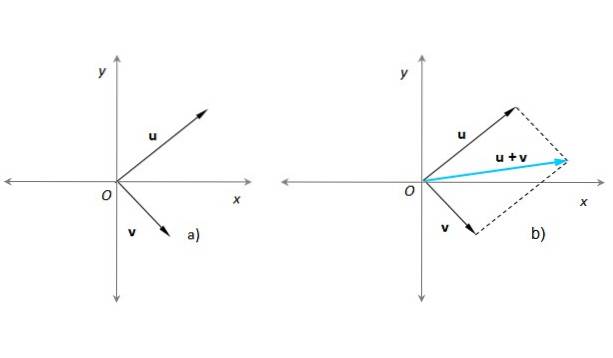
I figur 3b) er der konstrueret et parallelogram ved hjælp af stiplede linjer parallelt med eller allerede v. Den resulterende vektor har sin oprindelse ved O og slutter ved det punkt, hvor de stiplede linjer skærer hinanden. Denne procedure svarer fuldstændigt til den, der er beskrevet i det foregående afsnit..
Uddannelse
-Øvelse 1
Givet følgende vektorer, find den resulterende vektor ved hjælp af traversmetoden.
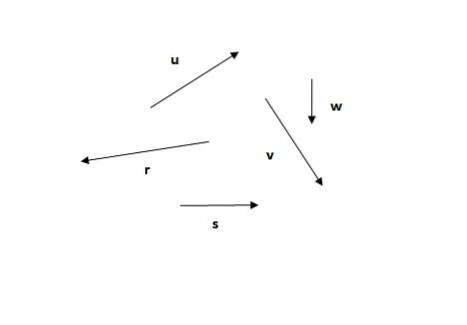
Opløsning
Traversemetoden er den første af de sete metoder. Husk at summen af vektorer er kommutativ (rækkefølgen af tilføjelserne ændrer ikke summen), så du kan starte med en hvilken som helst af vektorerne, for eksempel eller (figur 5a) eller r (figur 5b):
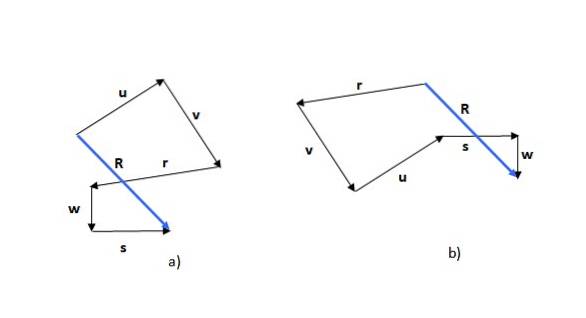
Den opnåede figur er en polygon, og den resulterende vektor (i blåt) kaldes R. Hvis du starter med en anden vektor, kan den form, der dannes, være anderledes, som det kan ses i eksemplet, men den resulterende vektor er den samme.
Øvelse 2
I den følgende figur er det kendt, at modulerne til vektorerne eller Y v henholdsvis er de u = 3 vilkårlige enheder og v = 1,8 vilkårlige enheder. Den vinkel, der eller form med den positive x-akse er 45º, mens v den danner 60º med y-aksen, som det ses på figuren. Find den resulterende vektor, størrelse og retning.
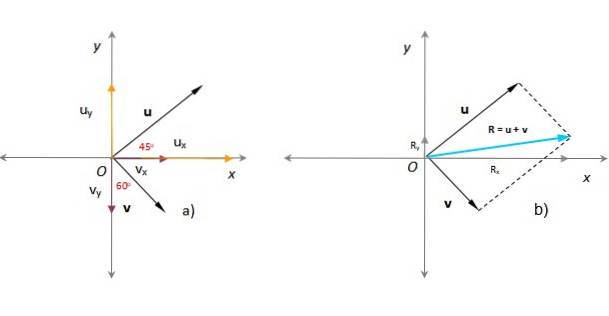
Opløsning
I det forrige afsnit blev den resulterende vektor fundet ved at anvende parallelogrammetoden (i turkis i figuren).
En nem måde at finde den resulterende vektor analytisk på er at udtrykke addendvektorerne med hensyn til deres kartesiske komponenter, hvilket er let, når modulus og vinkel er kendt, såsom vektorerne i dette eksempel:
ellerx = u. cos 45º = 3 x cos 45º = 2.12; ellerY = u. sin 45º = 3x sin 45º = 2.12
vx = v. sin 60º = 1,8 x sin 60º = 1,56; vY = -v. cos 60º = -1,8 x cos 60º = - 0,9
Vektorer eller Y v de er vektorer, der hører til flyet og har derfor to komponenter hver. Vektor u er i den første kvadrant, og dens komponenter er positive, mens vektor v er i den fjerde kvadrant; dens x-komponent er positiv, men dens projektion på den lodrette akse falder på den negative y-akse.
Beregning af de kartesiske komponenter i den resulterende vektor
Den resulterende vektor findes ved at tilføje algebraisk de respektive x- og y-komponenter for at opnå deres kartesiske komponenter:
Rx = 2,12 + 1,56 = 3,68
RY = 2,12 + (-0,9) = 1,22
Når de kartesiske komponenter er specificeret, er vektoren fuldt kendt. Den resulterende vektor kan udtrykkes med notationen i firkantede parenteser (seler):
R = < 3.68; 1.22> vilkårlige enheder
Notationen med firkantede parenteser bruges til at skelne en vektor fra et punkt i planet (eller i rummet). En anden måde at udtrykke den resulterende vektor analytisk på er ved hjælp af enhedsvektorerne jeg og j i flyet (jeg, j Y k i rummet):
R = 3,68 jeg + 1.22 j vilkårlige enheder
Da begge komponenter i den resulterende vektor er positive, er vektoren R tilhører den første kvadrant, som allerede var set grafisk før.
Den resulterende vektors størrelse og retning
Kendskab til de kartesiske komponenter beregnes størrelsen på R gennem den pythagoriske sætning, da den resulterende vektor R, sammen med dets R-komponenterx og RY danne en højre trekant:
Størrelse eller modul: R = (3,68to + 1.22to)½ = 3,88
Retning q med den positive x-akse som reference: q = arctan (RY / Rx) = arctg (1,22 /3,68) = 18,3 º
Referencer
- Tilføjelse af vektorer og regler. Hentet fra: newt.phys.unsw.edu.au
- Figueroa, D. Series: Physics for Sciences and Engineering. Bind 1. kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Gendannet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik for ingeniører. Statisk. 6. udgave. Continental Publishing Company. 15-53.
- Vector Addition Lommeregner. Hentet fra: www.1728.org



Endnu ingen kommentarer