
Samtidige vektorers egenskaber, eksempler og øvelser
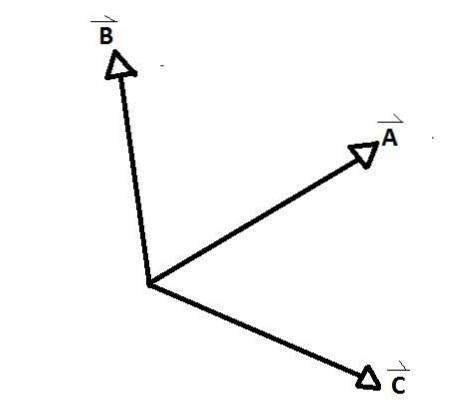
Det samtidige vektorer er grupper af vektorer, hvis akser falder sammen på et punkt og danner mellem hvert par af dem en intern og en ekstern vinkel. Et tydeligt eksempel ses i nedenstående figur, hvor A, B og C er vektorer, der er samtidige med hinanden.
D og E er ikke i modsætning til resten. Der er vinkler dannet mellem de samtidige vektorer AB, AC og CB. De kaldes forholdsvinkler mellem vektorerne.
Artikelindeks
- 1 Funktioner
- 2 Typer af vektorer
- 3 Vector notation
- 3.1 Cartesian
- 3.2 Polar
- 3.3 Analytisk
- 3.4 Sfærisk
- 4 Operationer med samtidige vektorer
- 4.1 Sum (A + B)
- 4.2 Forskel (A - B)
- 4.3 Skalarprodukt (A.B)
- 4.4 Vektorprodukt (A x B)
- 5 eksempler: øvelser løst
- 5.1 Øvelse 1
- 5.2 Øvelse 2
- 6 Foreslåede øvelser
- 7 Referencer
Egenskaber
-De har et fælles punkt, der falder sammen med deres oprindelse: alle størrelserne af de samtidige vektorer starter fra et fælles punkt til deres respektive ekstremer..
-Oprindelsen betragtes som vektorens handlingspunkt: der skal etableres et handlingspunkt, som vil blive direkte påvirket af hver af de samtidige vektorer.
-Hans domæne i plan og rum er Rto og R3 henholdsvis: de samtidige vektorer er frie til at dække hele det geometriske rum.
-Det tillader forskellige notationer i den samme gruppe af vektorer. Ifølge undersøgelsesgrene findes forskellige notationer i operationer med vektorer.
Typer af vektorer
Grenen af vektorer har flere underinddelinger, hvoraf nogle kan navngives: parallel, vinkelret, coplanar, tilsvarende, modsat og enhed. Samtidige vektorer er angivet her, og som alle de ovennævnte har de mange applikationer inden for forskellige videnskaber..
De er meget almindelige i studiet af vektorer, fordi de repræsenterer en nyttig generalisering i operationerne med dem. Både i planet og i rummet bruges samtidige vektorer ofte til at repræsentere forskellige elementer og studere deres indflydelse på et bestemt system..
Vector notation
Der er flere måder at repræsentere et vektorelement på. De vigtigste og mest kendte er:
Kartesisk
Foreslået af den samme matematiske tilgang angiver det vektorerne med en tredobbelt svarende til størrelsen af hver akse (x, y, z)
A: (1, 1, -1) Mellemrum A: (1, 1) Fly
Polar
De tjener kun til at betegne vektorer i planet, selvom de i den integrerede beregning tildeles dybdekomponenten. Den er sammensat med en lineær størrelse r og en vinkel i forhold til polaraksen Ɵ.
A: (3, 450 Plan A: (2, 450 , 3) Rum
Analytisk
De definerer størrelsen af vektoren ved hjælp af versores. Versores (i + j + k) repræsenterer enhedsvektorerne svarende til akserne X, Y Y
A: 3i + 2j - 3k
Sfærisk
De ligner polær notation, men med tilføjelsen af en anden vinkel, der fejer over flyet xy symboliseret ved δ.
A: (4, 60eller , π / 4)
Samtidige vektoroperationer
Samtidige vektorer bruges mest til at definere operationer mellem vektorer, fordi det er lettere at sammenligne elementerne i vektorerne, når de præsenteres samtidigt..
Sum (A + B)
Summen af samtidige vektorer sigter mod at finde den resulterende vektor Vr. Hvilket ifølge undersøgelsesgrenen svarer til en endelig handling
For eksempel: 3 strenge A, B, C er bundet til en boks, hver ende af strengen holdes af et emne. Hver af de 3 emner skal trække rebet i en anden retning end de andre 2.
A: (økse, ay, az) B: (bx, ved, bz) C: (cx, cy, cz)
A + B + C = (ax + bx + cx; ay + ved + cy; az + bz + cz) = Vr
Kassen kan derfor kun bevæge sig i en retning Vr angiver retning og retning af kassen.
Forskel (A - B)
Der er mange kriterier med hensyn til forskellen mellem vektorer, mange forfattere vælger at udelukke den og angiver, at kun summen mellem vektorer er angivet, hvor forskellen handler om summen af den modsatte vektor. Sandheden er, at vektorerne kan trækkes algebraisk.
A: (økse, ay, az) B: (bx, ved, bz)
A - B = A + (-B) = (ax-bx; ay-by; az-bz) = [ax + (-bx); ay + (-by); az + (-bz)]
Skalarprodukt (A.B)
Også kendt som et punktprodukt, genererer det en skalarværdi, der kan relateres til forskellige størrelser afhængigt af undersøgelsesgrenen..
For geometri angiver arealet af parallelogrammet dannet af paret af samtidige vektorer gennem parallelogrammetoden. For mekanisk fysik definerer det arbejde, der udføres af en kraft F når man bevæger en krop en afstand Ar.
ѡ = F . Ar
Som navnet antyder, genererer den en skalarværdi og defineres som følger:
Lad vektorerne A og B være
A: (økse, ay, az) B: (bx, ved, bz)
-Analytisk form:
(A. B) = | A |. | B | .Cos θ
Hvor θ er den indvendige vinkel mellem begge vektorer
-Algebraisk form:
(A. B) = (ax.bx + ay.by + az.bz)
Tværprodukt (A x B)
Korsproduktet eller punktproduktet mellem to vektorer definerer en tredje vektor C som har kvaliteten af at være vinkelret på B Y C. I fysik definerer momentvektoren τ basiselement for rotationsdynamik.
-Analytisk form:
| A x B | = | A |. | B | .Sen θ
-Algebraisk form:
(A x B) = = (Ax. By - ay. Bx) - (ax. Bz - az. Bx) j + (ax. af - ay. bx) k
-Relativ bevægelse: rA / B
Grundlaget for relativitet er relativ bevægelse, og samtidige vektorer er grundlaget for relativ bevægelse. Relative positioner, hastigheder og accelerationer kan udledes ved at anvende følgende ideerækkefølge.
r A / B = rTIL - rB ; Relativ position for A i forhold til B
v A / B = vTIL - vB ; Relativ hastighed af A i forhold til B
til A / B = aTIL - tilB ; Relativ acceleration af A i forhold til B
Eksempler: øvelser løst
Øvelse 1
Lad A, B og C være samtidige vektorer.
A = (-1, 3, 5) B = (3, 5, -2) C = (-4, -2, 1)
-Definer den resulterende vektor Vr = 2A - 3B + C.
2A = (2 (-1), 2 (3), 2 (5)) = (-2, 6, 10)
-3B = (-3 (3), -3 (5), -3 (-2)) = (-9, -15, 6)
Vr = 2A + (-3B) + C = (-2, 6, 10) + (-9, -15, 6) + (-4, -2, 1)
Vr = ([-2 + (- 9) + (- 4)]; [6 + (- 15) + (- 2)]; (10 + 6 + 1))
Vr = (-15, -11, 17)
-Definer prikproduktet (A.C)
(A.C) = (-1, 3, 5). (-4, -2, 1) = (-1) (-4) + 3 (-2) + 5 (1) = 4-6 + 5
(A. C) = 3
-Beregn vinklen mellem A og C
(A. C) = | A |. | C |. Cos θ Hvor θ er den korteste vinkel mellem vektorerne
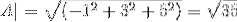
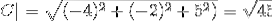
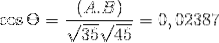
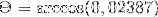
θ = 88,630
-Find en vektor vinkelret på A og B
Til dette er det nødvendigt at definere vektorproduktet mellem (-1, 3, 5) og (3, 5, -2). Som forklaret før konstrueres en 3 x 3 matrix, hvor den første række er sammensat af de tredobbelte enhedsvektorer (i, j, k). Derefter består 2. og 3. række af vektorerne, der skal betjenes, under overholdelse af den operationelle rækkefølge.
(A x B) = = [(-1). 5 - (3. 3)] jeg - [(-1). (-2) - (5. 3)] j + [(-1). 5 - (3. 3)] k
(A x B) = (-5 - 9) jeg - (2 - 15) j + (-5 - 9) k
(A x B) = -14 I + 13 j - 14 k
Øvelse 2
Lad Vtil og Vb hastighedsvektorerne for henholdsvis A og B. Beregn hastigheden af B set fra A..
Vtil = (3, -1, 5) Vb = (2, 5, -3)
I dette tilfælde kræves den relative hastighed af B i forhold til A VB / A
VB / A = VB - VTIL
VB / A = (2, 5, -3) - (3, -1, 5) = (-1, 6, -8)
Dette er hastighedsvektoren for B set fra A. Hvor en ny vektor af hastigheden for B er beskrevet under henvisning fra en observatør placeret ved A og bevæger sig med hastigheden A.
Foreslåede øvelser
1-konstruer 3 vektorer A, B og C, der er samtidige og relaterer 3 operationer imellem dem gennem en praktisk øvelse.
2-Lad vektorerne A: (-2, 4, -11), B: (1, -6, 9) og C: (-2, -1, 10). Find vektorer vinkelret på: A og B, C og B, summen A + B + C.
4-Bestem 3 vektorer, der er vinkelrette på hinanden uden at tage hensyn til koordinatakserne.
5-Definer arbejdet udført af en kraft, der løfter en masse på 5 kg, fra bunden af en dybde på 20 m.
6-Vis algebraisk, at subtraktion af vektorer er lig med summen af den modsatte vektor. Retfærdiggør dine postulater.
7-Betegn en vektor i alle notationer udviklet i denne artikel. (Kartesisk, polær, analytisk og sfærisk).
8-De magnetiske kræfter, der udøves på en magnet, der hviler på et bord, er givet af følgende vektorer; V: (5, 3, -2), T: (4, 7, 9), H: (-3, 5, -4). Bestem, i hvilken retning magneten bevæger sig, hvis alle magnetiske kræfter virker på samme tid.
Referencer
- Euklidisk geometri og transformation. Clayton W. Dodge. Courier Corporation, 1. jan 2004
- Sådan løses anvendt matematikproblemer L. Moiseiwitsch. Courier Corporation, 10. apr 2013
- Grundlæggende begreber i geometri. Walter Prenowitz, Meyer Jordan. Rowman & Littlefield, 4. okt 2012
- Vektorer. Rocío Navarro Lacoba, 7. juni. 2014
- Lineær algebra. Bernard Kolman, David R. Hill. Pearson Education, 2006


Endnu ingen kommentarer