
Gratis vektorer egenskaber, eksempler, øvelser
Det gratis vektorer De er dem, der er fuldt specificeret af deres størrelse, deres retning og deres sans, uden at det er nødvendigt at angive et anvendelsessted eller en bestemt oprindelse.
Da uendelige vektorer kan tegnes på denne måde, er en fri vektor ikke en enkelt enhed, men et sæt parallelle og identiske vektorer, der er uafhængige af, hvor de er..
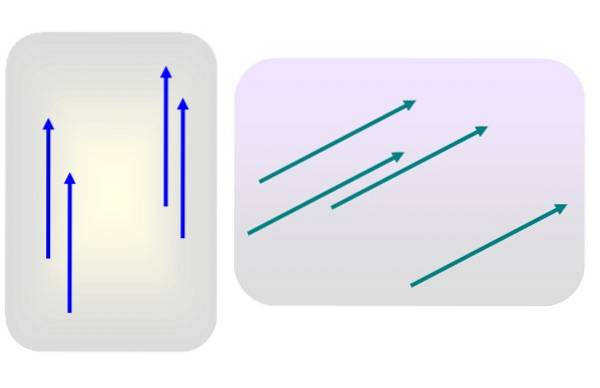
Lad os sige, at vi har flere vektorer med størrelsesorden 3 rettet lodret opad eller af størrelse 5 og skråt mod højre, som i figur 1.
Ingen af disse vektorer anvendes specifikt på noget tidspunkt. Derefter er en hvilken som helst af de blå eller grønne vektorer repræsentativ for deres respektive gruppe, da deres egenskaber - modul, retning og sans - slet ikke ændrer sig, når de overføres til et andet sted i planet..
En fri vektor betegnes f.eks. Normalt med trykt, lille bogstav i trykt tekst v. Eller med små bogstaver og en pil på toppen, hvis det er håndskrevet tekst.
Artikelindeks
- 1 Eksempler
- 1.1 Egenskaber og egenskaber
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2 Øvelse 2
- 3 Referencer
Eksempler
Fordelen ved gratis vektorer er, at de kan bevæges gennem planet eller gennem rummet og opretholde deres egenskaber, da enhver repræsentant for sættet er lige så gyldig.
Derfor bruges de ofte i fysik og mekanik. For eksempel for at angive den lineære hastighed for et bevægeligt faststof er det ikke nødvendigt at vælge et bestemt punkt på objektet. Så hastighedsvektoren opfører sig som en fri vektor.
Et andet eksempel på en fri vektor er styrken. EN par Den består af to kræfter af samme størrelse og retning, men af modsatte retninger, påført på forskellige punkter på et fast stof. Virkningen af et par er ikke at oversætte objektet, men at forårsage en rotation takket være øjeblik produceret.
Figur 2 viser et par kræfter påført et ratt. Gennem kræfterne F1 Y Fto, Der oprettes et drejningsmoment, der drejer svinghjulet rundt om midten og med uret.
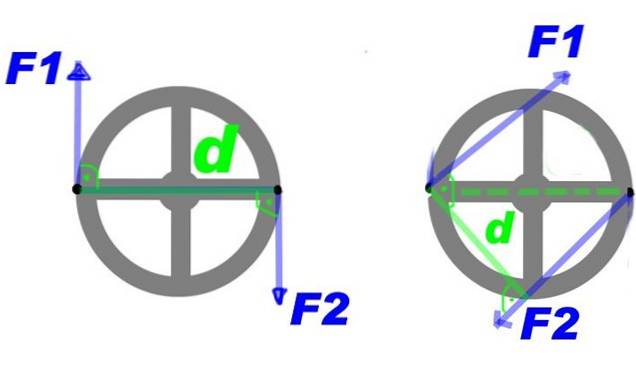
Du kan foretage nogle ændringer i drejningsmomentet og stadig få den samme roterende effekt, for eksempel at øge kraften, men mindske afstanden mellem dem. Eller vedligehold kraften og afstanden, men anvend momentet på et andet par punkter på rattet, dvs. drej drejningsmomentet rundt om midten.
Øjeblikket af styrkerparret eller simpelthen par, er en vektor, hvis modul er Fd og er rettet vinkelret på svinghjulets plan. I eksemplet vist ved konvention har urets rotation en negativ forstand.
Egenskaber og egenskaber
I modsætning til den gratis vektor v, vektorerne AB Y CD de er faste (se figur 3), da de har et specificeret startpunkt og ankomstpunkt. Men da de er holdemæssige med hinanden og igen med vektoren v, er repræsentative for den frie vektor v.

De vigtigste egenskaber ved gratis vektorer er følgende:
-Enhver vektor AB (se figur 2) er som sagt repræsentativ for den frie vektor v.
-Modulet, retningen og sansen er den samme i enhver repræsentant for den frie vektor. I figur 2 er vektorerne AB Y CD repræsenterer den frie vektor v og de er teamorienterede.
-Givet et punkt P i rummet, er det altid muligt at finde en repræsentant for den frie vektor v hvis oprindelse er i P, og repræsentanten er unik. Dette er den vigtigste egenskab ved gratis vektorer, og den der gør dem så alsidige.
-En nullfri vektor er betegnet som 0 y er sættet af alle vektorer, der mangler størrelse, retning og sans.
-Hvis vektoren AB repræsenterer fri vektor v, derefter vektoren BA repræsenterer fri vektor -v.
-Notationen vil blive brugt V3 at betegne sættet med alle gratis rumvektorer og Vto at udpege alle gratis vektorer i flyet.
Løst øvelser
Med gratis vektorer kan følgende operationer udføres:
-Sum
-Subtraktion
-Multiplikation af skalar med en vektor
-Skalarprodukt mellem to vektorer.
-Kryds produkt mellem to vektorer
-Lineær kombination af vektorer
Og mere.
-Øvelse 1
En studerende prøver at svømme fra et punkt på bredden af en flod til et andet, der er direkte modsat. For at opnå dette er der intet direkte med en hastighed på 6 km / t i en vinkelret retning, men strømmen har dog en hastighed på 4 km / t, der afbøjer den.
Beregn svømmerens resulterende hastighed, og hvor meget han afbøjes af strømmen.
Opløsning
Svømmerens resulterende hastighed er vektorsummen af hans hastighed (i forhold til floden, tegnet lodret opad) og hastigheden af floden (trukket fra venstre mod højre), som udføres som angivet i nedenstående figur:
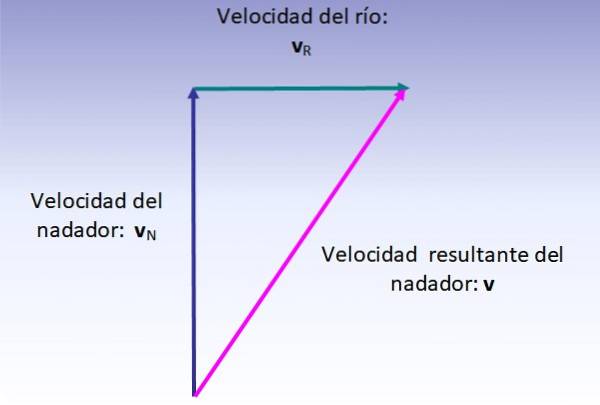
Størrelsen af den resulterende hastighed svarer til hypotenusen i den viste trekant, derfor:
v = (6to + 4to) ½ km / t = 7,2 km / t
Retningen kan beregnes ved hjælp af vinklen i forhold til vinkelret på kysten:
α = arctg (4/6) = 33,7º eller 56,3º i forhold til kysten.
Øvelse 2
Find øjeblikket for parret vist i figuren:
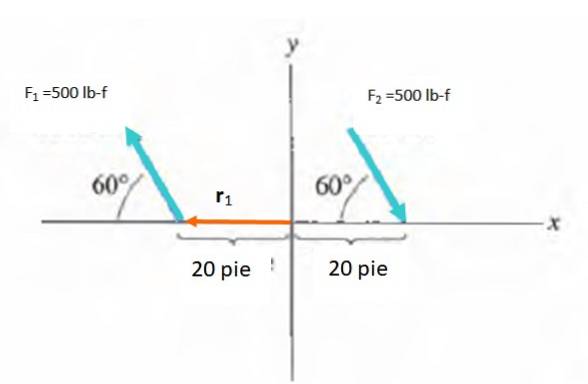
Opløsning
Øjeblikket beregnes af:
M = r x F
Momentets enheder er lb-f.ft. Da drejningsmomentet er i skærmens plan, dirigeres øjeblikket vinkelret på det, enten udad eller indad..
Da drejningsmomentet i eksemplet har en tendens til at dreje objektet, hvorpå det påføres (som ikke er vist på figuren) med uret, betragtes dette øjeblik som at pege mod indersiden af skærmen med et negativt tegn.
Momentets størrelse er M = F.d. i a, hvor a er vinklen mellem kraften og vektoren r. Du skal vælge et punkt, som øjeblikket skal beregnes med, som er en fri vektor. Oprindelsen til referencesystemet vælges derfor r går fra O til anvendelsespunktet for hver kraft.
M1 = Mto = -Fdsen60º = -500. 20 .sin 60º lb-f. ft = -8660,3 lb-f. fod
Nettomomentet er summen af M1 og Mto: -17329,5 lb-f. fod.
Referencer
- Beardon, T. 2011. En introduktion til vektorer. Hentet fra: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Bind 1. kinematik. 31-68.
- Fysisk. Modul 8: Vektorer. Gendannet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanik for ingeniører. Statisk. 6. udgave. Continental Publishing Company. 15-53.
- Vector Addition Lommeregner. Gendannet fra: 1728.org
- Vektorer. Gendannet fra: en.wikibooks.org



Endnu ingen kommentarer