
Areolar hastighed, hvordan det beregnes og øvelser løses
Det areolar hastighed er området fejet pr. tidsenhed og er konstant. Det er specifikt for hver planet og stammer fra beskrivelsen af Keplers anden lov i matematisk form. I denne artikel vil vi forklare, hvad det er, og hvordan det beregnes.
Bommen, der repræsenterer opdagelsen af planeter uden for solsystemet, har genoplivet interessen for planetbevægelse. Intet tyder på, at disse exo-planeter følger andre love end dem, der allerede er kendt og gyldige i solsystemet: Keplers love..
Johannes Kepler var astronomen, der uden hjælp fra teleskopet og ved hjælp af observationer fra sin mentor Tycho Brahe skabte en matematisk model, der beskriver planetenes bevægelse omkring solen..
Han efterlod denne model inkarneret i de tre love, der bærer hans navn, og som forbliver lige så gyldige i dag som i 1609, da han etablerede de to første og i 1618, den dato, hvor han erklærede den tredje..
Artikelindeks
- 1 Keplers love
- 2 Hvorfor bevæger planeterne sig elliptisk rundt om solen?
- 3 Størrelsen af en planetes lineære hastighed er ikke konstant
- 4 Areolar hastighed
- 5 Beregning af lineær hastighed og areolar hastighed
- 5.1 Øvelse
- 6 Bibliografi
Keplers love
I dagens sprog lyder Keplers tre love således:
1. Banerne på alle planeterne er elliptiske, og solen er i fokus.
2. Positionsvektoren fra solen til en planet fejer lige store områder på lige tid.
3. Kvadratet for en planets omløbsperiode er proportionalt med terningen på den beskrevne ellips semi-hovedakse..
En planet vil have en lineær hastighed, ligesom ethvert kendt objekt i bevægelse. Og der er endnu mere: Når man skriver Keplers anden lov i matematisk form, opstår et nyt koncept kaldet areolær hastighed, typisk for hver planet..
Hvorfor bevæger planeterne sig elliptisk rundt om solen?
Jorden og de andre planeter bevæger sig rundt om solen takket være det faktum, at den udøver en kraft på dem: tyngdekraftsattraktionen. Det samme sker med enhver anden stjerne og planeterne, der udgør dens system, hvis den har dem..
Dette er en kraft af typen kendt som en central styrke. Vægt er en central kraft, som alle er fortrolige med. Objektet, der udøver den centrale kraft, det være sig solen eller en fjern stjerne, tiltrækker planeterne mod dets centrum, og de bevæger sig i en lukket kurve.
I princippet kan denne kurve tilnærmes som en omkreds, ligesom Nicolás Copernicus, en polsk astronom, der skabte den heliocentriske teori..
Den ansvarlige kraft er tyngdekraftsattraktionen. Denne kraft afhænger direkte af stjernens og planetens masser og er omvendt proportional med kvadratet for afstanden, der adskiller dem..
Problemet er ikke så let, for i et solsystem interagerer alle elementerne på denne måde og tilføjer kompleksiteten til sagen. Desuden er de ikke partikler, da stjerner og planeter har målelig størrelse..
Af denne grund er det centrale punkt i kredsløb eller kredsløb, som planeterne rejser, ikke ligefrem centreret på stjernen, men på et punkt kendt som tyngdepunktet for sol-planet-systemet..
Den resulterende bane er elliptisk. Følgende billede viser det, idet vi tager jorden og solen som et eksempel:
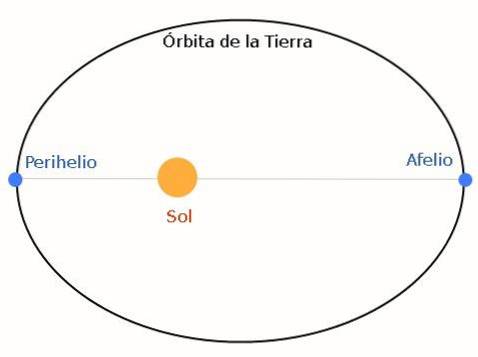
Aphelion er den fjerneste position på Jorden fra Solen, mens periheliet er det nærmeste punkt. Ellipsen kan være mere eller mindre flad afhængigt af stjerneplanetsystemets egenskaber..
Aphelion- og perihelionværdierne varierer årligt, da de andre planeter forårsager forstyrrelser. For andre planeter kaldes disse positioner henholdsvis apoaster og periaster..
Størrelsen af en planetes lineære hastighed er ikke konstant
Kepler opdagede, at når en planet kredser om solen, fejer den under dens bevægelse lige områder op på lige tid. Figur 2 viser grafisk betydningen af dette:
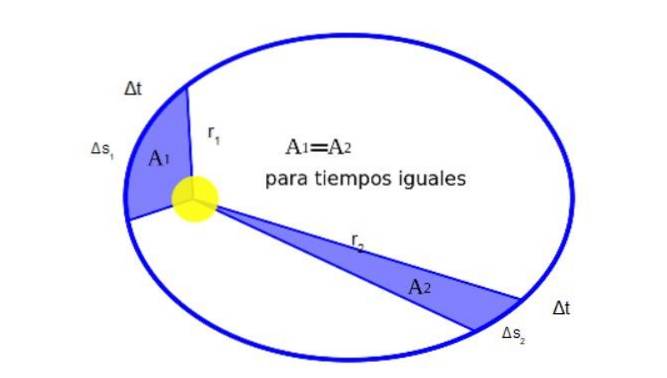
Matematisk er det faktum, at A1 være lig med Ato udtrykkes således:

De tilbagelagte buer Δs er små, så hvert område kan tilnærme sig det, der findes i en trekant:
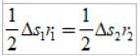
Da Δs =vΔt, hvor v er planetens lineære hastighed på et givet punkt ved at erstatte har vi:
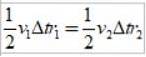
Og da tidsintervallet Δt er det samme, opnår vi:
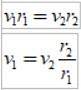
Som rto > r1, derefter v1 > vto, med andre ord er en planetes lineære hastighed ikke konstant. Faktisk går jorden hurtigere, når den er i perihel, end når den er i aphelion..
Derfor er den lineære hastighed på jorden eller på en hvilken som helst planet omkring solen ikke en størrelse, der tjener til at karakterisere bevægelsen af planeten..
Areolar hastighed
Keplers anden lov antyder en ny størrelse kaldet areolar hastighed. Det defineres som det område, der fejes pr. Tidsenhed og er konstant. For at beregne det anvendes følgende figur:
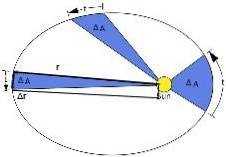
Et lille område fejet af Jorden vælges, mens man laver dets elliptiske kredsløb, som vi vil betegne som ΔA. Den nødvendige tid til dette er Δt.
Figur 3 viser Jordens positionsvektor i forhold til Solen, betegnet med r. Når Jorden bevæger sig, oplever den en forskydning Δr.
Dette område svarer til halvdelen af arealet af rektanglet vist i figur 3:
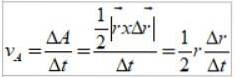
Kvotienten Δr / Δt er nøjagtigt Jordens lineære hastighed, så areolær hastighed er som:
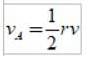
Enhederne i vTIL i det internationale system er de:
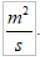
Bemærk, at selvom både r og v varierer, forbliver produktet konstant. Dette gør areolær hastighed til en meget tilstrækkelig størrelse til at karakterisere bevægelsen af en planet omkring dens stjerne..
Produktet af r og v er størrelsen af vinkelmomentet L, således at areolær hastighed kan udtrykkes som:
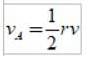
Beregning af lineær hastighed og areolar hastighed
Med det følgende eksempel viser vi, hvordan man beregner areolær hastighed, når nogle parametre for planetbevægelse er kendt:
Dyrke motion
En exo-planet bevæger sig omkring sin sol efter en elliptisk bane i henhold til Keplers love. Når den er i periasteren, er dens radiusvektor r1 = 4 107 km, og når det er i apoastro, er det rto = 15 107 km. Den lineære hastighed ved sin periaster er v1 = 1000 km / s.
Beregn:
A) Størrelsen af hastigheden ved apoastro.
B) Exo-planetens areolære hastighed.
C) Længden af ellipsens semi-hovedakse.
Svar til)
Ligningen bruges:
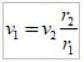
hvor numeriske værdier er substitueret.
Hvert udtryk identificeres som følger:
v1 = hastighed i apoastro; vto = hastighed i periasteren; r1= afstand fra apoastro,
rto= afstand fra periaster.
Med disse værdier får du:

Svar B)
Ligningen at bruge er
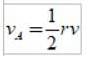
hvori parret af værdier r og v for periaster eller apoaster kan erstattes, da vTIL er en konstant af planeten:

Svar C)
Længden af ellipsens semi-hovedakse er halve som apoaster og periaster:
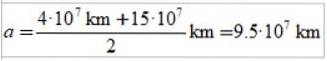
Bibliografi
- Serway, R., Jewett, J. (2008). Fysik til videnskab og teknik. Bind 1. Mexico. Cengage Learning Editors. 367-372.
- Stern, D. (2005). Keplers tre love om planetarisk bevægelse. Gendannet fra pwg.gsfc.nasa.gov
- Bemærk: den foreslåede øvelse blev taget og ændret fra følgende tekst i en McGrawHill-bog. Desværre er det et isoleret kapitel i pdf-format uden titlen eller forfatteren: mheducation.es/bcv/guide/capitulo/844817027X.pdf

Endnu ingen kommentarer