
Gravity acceleration hvad det er, hvordan det måles og øvelser
Det tyngdeacceleration eller tyngdeacceleration defineres som intensiteten af jordens tyngdefelt. Det vil sige den kraft, den udøver på ethvert objekt pr. Masseenhed.
Det er betegnet med det nu velkendte bogstav g, og dets omtrentlige værdi i nærheden af jordoverfladen er 9,8 m / sto. Denne værdi kan opleve små variationer med geografisk bredde og også med højde i forhold til havets overflade..

Tyngdeaccelerationen har, ud over at have den førnævnte størrelse, retning og sans. Faktisk er den rettet lodret mod midten af jorden.
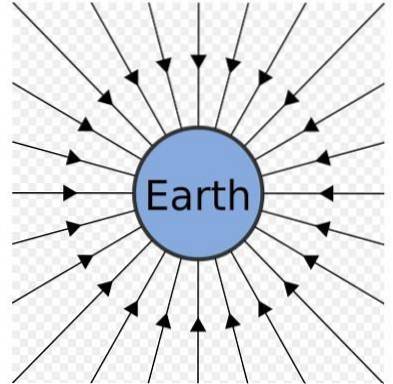
Jordens tyngdefelt kan repræsenteres som et sæt radiale linjer, der peger mod midten, som vist i den foregående figur.
Artikelindeks
- 1 Hvad er tyngdeacceleration??
- 1.1 Loven om universel tyngdekraft
- 2 Hvordan måles tyngdekraften på forskellige planeter?
- 2.1 Eksperiment for at bestemme værdien af g
- 2.2 Standardværdi af g på jorden, på månen og på Mars
- 2.3 Tyngdekraften på månen
- 2.4 Tyngdekraften på Mars
- 3 Øvelse løst: det faldende æble
- 4 Referencer
Hvad er tyngdeacceleration?
Værdien af tyngdeaccelerationen på Jorden eller på enhver anden planet svarer til intensiteten af tyngdefeltet, den producerer, hvilket ikke afhænger af objekterne omkring den, men kun af dens egen masse og radius..
Tyngdeaccelerationen defineres ofte som den acceleration, som enhver genstand oplever i frit fald i nærheden af jordens overflade..
I praksis er dette, hvad der næsten altid sker, som vi vil se i de følgende afsnit, hvor Newtons lov om universel tyngdekraft vil blive brugt..
Newton siges at have opdaget denne berømte lov, mens han mediterede på faldende kroppe under et træ. Da han følte æblets slag på hovedet, vidste han straks, at den kraft, der får æblet til at falde, er den samme, der får Månen til at kredser om Jorden.
Loven om universel tyngdekraft
Uanset om legenden om æblet var sandt eller ej, indså Newton, at størrelsen af tyngdekraftens tiltrækningskraft mellem to objekter, for eksempel mellem jorden og månen eller jorden og æblet, skulle afhænge af deres masser:




Tyngdekraftens egenskaber
Gravitationskraften er altid attraktiv; de to organer, det påvirker, tiltrækker hinanden. Det modsatte er ikke muligt, da himmellegemernes baner er lukkede eller åbne (for eksempel kometer), og en frastødende kraft aldrig kan frembringe en lukket bane. Så masserne tiltrækker altid, uanset hvad.
En forholdsvis god tilnærmelse til Jordens sande form (m1) Og af månen eller æblet (mto) er at antage, at de har en sfærisk form. Følgende figur er en gengivelse af dette fænomen.

Her både den kraft, der udøves af m1 Omkring mto, som den, der mto Omkring m1, begge af samme størrelse og rettet langs den linje, der slutter sig til centrene. De annulleres ikke, da de anvendes på forskellige objekter.
I alle de følgende afsnit antages det, at objekterne er homogene og sfæriske, derfor falder deres tyngdepunkt sammen med deres geometriske centrum. Det kan antages, at al massen er koncentreret lige der.
Hvordan måler du tyngdekraften på forskellige planeter?
Tyngdekraften kan måles med et gravimeter, en tyngdekraftsmåler, der anvendes i geofysiske gravimetriske undersøgelser. I øjeblikket er de meget mere sofistikerede end originalerne, men i starten var de baseret på pendulet.
Pendulet består af et tyndt, let og uudvideligt reb med længde L. Den ene af dens ender er fastgjort til en støtte, og en masse m hænges op fra den anden..
Når systemet er i ligevægt, hænger massen lodret, men når den adskilles fra den, begynder den at svinge og udfører en frem og tilbage bevægelse. Tyngdekraften er ansvarlig for det. For alt det følgende er det gyldigt at antage, at tyngdekraften er den eneste kraft, der virker på pendulet.
Perioden T for pendulets svingning for små svingninger er givet ved følgende ligning:


Eksperiment for at bestemme værdien af g
Materialer
- 1 metalkugle.
- Reb af flere forskellige længder, mindst 5.
- Målebånd.
- Transportør.
- Kronometer.
- Et beslag til fastgørelse af pendulet.
- Grafpapir eller computerprogram med regneark.
Behandle
- Vælg en af strengene, og saml pendulet. Mål længden af strengen + kuglens radius. Dette vil være længden L..
- Fjern pendulet fra ligevægtspositionen med ca. 5 grader (mål det med vinkelmåleren) og lad det svinge.
- Start stopuret samtidigt, og mål tiden på 10 svingninger. Skriv resultatet ned.
- Gentag ovenstående procedure for de andre længder.
- Find den tid T det tager for pendulet at svinge (divider hvert af ovenstående resultater med 10).
- Firkant hver opnået værdi med opnåelse af Tto
- På grafpapir tegner du hver værdi af Tto på den lodrette akse mod den respektive værdi af L på den vandrette akse. Vær konsekvent med enhederne og glem ikke at tage højde for fejltagelsen af de anvendte instrumenter: målebånd og stopur..
- Tegn den bedste linje, der passer til de afbildede punkter.
- Find skråningen m af nævnte linje ved hjælp af to punkter, der hører til den (ikke nødvendigvis eksperimentelle punkter). Tilføj den eksperimentelle fejl.
- Ovenstående trin kan udføres med et regneark og mulighed for at konstruere og tilpasse en lige linje.
- Fra hældningsværdien til rydde værdien af g med sin respektive eksperimentelle usikkerhed.
Standardværdi af g på jorden, på månen og på Mars
Standardværdien af tyngdekraften på Jorden er: 9,81 m / sto, på 45º nordlig bredde og ved havets overflade. Da Jorden ikke er en perfekt sfære, er værdierne af g variere lidt, være højere ved polerne og lavere ved ækvator.
De, der ønsker at kende værdien i deres lokalitet, kan finde den opdateret på webstedet for det tyske metrologiske institut PTB (Physikalisch-Technische Bundesanstalt), i afsnittet Tyngdekraftsinformationssystem (KRIDT).
Tyngdekraften på månen
Månens tyngdefelt er blevet bestemt ved at analysere radiosignaler fra rumsonder, der kredser om satellitten. Dens værdi på månens overflade er 1,62 m / sto
Tyngdekraften på mars
Værdien af gP for en planet afhænger den af dens masse M og dens radius R som følger:

Derfor:

For planeten Mars er følgende data tilgængelige:
M = 6,4185 x 102. 3 kg
R = 3390 km
G = 6,67 x 10-elleve N.mto/ kgto
Med disse data ved vi, at tyngdekraften på Mars er 3,71 m / sto. Naturligvis kan den samme ligning anvendes med data fra månen eller enhver anden planet og således estimere værdien af dens tyngdekraft.
Træning løst: det faldende æble
Antag at både jorden og et æble er kugleformede. Jordens masse er M = 5,98 x 1024 kg og dens radius er R = 6,37 x 106 m. Massen af æblet er m = 0,10 kg. Antag at der ikke er nogen anden kraft end tyngdekraften. Fra Newtons lov om universel tyngdekraft finder du:
a) Den tyngdekraft, som Jorden udøver på æblet.
b) Den acceleration, æblet oplever, når det frigives fra en bestemt højde, ifølge Newtons anden lov.
Opløsning
a) Æblet (angiveligt sfærisk, ligesom Jorden) har en meget lille radius sammenlignet med Jordens radius og er nedsænket i dets tyngdefelt. Den følgende figur er åbenbart ikke i målestok, men der er et diagram over tyngdefeltet g, og styrken F udøvet af jorden på æblet:

Ved at anvende Newtons lov om universel tyngdekraft kan afstanden mellem centrene betragtes som omtrent den samme værdi som jordens radius (den højde, hvorfra æblet falder, er også ubetydelig sammenlignet med jordens radius). Derfor:

b) Ifølge Newtons anden lov er størrelsen af den kraft, der udøves på æblet:
F = ma = mg
Hvis værdi er 0,983 N ifølge den tidligere beregning. Ved at sidestille begge værdier og derefter løse for accelerationens størrelse får vi:
mg = 0,983 N
g = 0,983 N / 0,10 kg = 9,83 m / sto
Dette er en meget god tilnærmelse til standardværdien af tyngdekraften.
Referencer
- Giancoli, D. (2006). Fysik: Principper med applikationer. Sjette udgave. Prentice Hall. 118-122.
- Hewitt, Paul. (2012). Konceptuel fysik. Femte udgave. Pearson. 91 - 94.
- Rex, A. (2011). Grundlæggende om fysik. Pearson. 213-221.



Endnu ingen kommentarer