Det øjeblikkelig acceleration Det er den ændring, som hastigheden oplever pr. Tidsenhed på hvert øjeblik af bevægelsen. I det nøjagtige øjeblik, hvordragster”Af billedet blev fotograferet, bar det en acceleration på 29,4 m / sto. Dette betyder, at dens hastighed på det tidspunkt blev øget med 29,4 m / s i løbet af 1 s. Dette svarer til 105 km / t på kun 1 sekund.
En dragster-konkurrence er let modelleret, forudsat at racerbilen er et punktobjekt. P der bevæger sig i en lige linje. På denne linje vælges en akse orienteret med oprindelse ELLER at vi kalder aksenOKSE) eller bare akse x.
De kinematiske variabler, der definerer og beskriver bevægelsen, er:
De er alle vektormængder. Derfor har de en størrelse, en retning og en sans.
I tilfælde af retlinet bevægelse er der kun to mulige retninger: positiv (+) i retning af (OKSE) eller negativ (-) i den modsatte retning af (OKSE). Derfor er det muligt at afstå fra den formelle vektornotation og bruge tegnene til at indikere følelsen af størrelsen.
Artikelindeks
Antag det i øjeblikket t partiklen har hastighed v (t) og i øjeblikket t ' dens hastighed er v (t ').
Så den ændring, som hastigheden havde i den periode, var Δv = v (t ') - v (t). Derfor er accelerationen i tidsforløbet Δt = t '- t , ville blive givet af kvotienten:
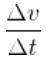
Denne kvotient er den gennemsnitlige acceleration vedm i tidsperioden Δt mellem øjeblikket t og t '.
Hvis vi ville beregne accelerationen lige på tidspunktet t, så skulle t 'være en ubetydelig større mængde end t. Med denne Δt, som er forskellen mellem de to, skal den være næsten nul.
Matematisk er det angivet som følger: Δt → 0 og det opnås:
JEG) En partikel bevæger sig langs X-aksen med konstant hastighed v0 = 3 m / s. Hvad bliver accelerationen af partiklen?
Derivatet af en konstant er nul, derfor er accelerationen af en partikel, der bevæger sig med konstant hastighed nul.
II) En partikel bevæger sig på aksen x og dens hastighed ændres med tiden i henhold til følgende formel:
v (t) = 2-3 t
Hvor hastighed måles i m / s og tid i s. Hvad vil være accelerationen af partiklen?
)
Resultatet fortolkes således: i ethvert øjeblik er accelerationen -3 m / s.
Mellem instanserne 0 s og 2/3 s er hastigheden positiv, mens accelerationen er negativ, det vil sige i det interval reducerer partiklen sin hastighed eller aftager.
I øjeblikket 2/3 s bliver dens hastighed nul, men da der forbliver en acceleration på -3 m / s, vender hastigheden fra det øjeblik (den bliver negativ).
I øjeblikket efter ⅔ s accelererer partiklen, da hver gang dens hastighed bliver mere negativ, dvs. dens hastighed (hastighedsmodul) vokser.
III) Figuren viser en kurve, der repræsenterer hastigheden som en funktion af tiden for en partikel, der bevæger sig langs X-aksen. Find tegnet på accelerationen til tider t1, tto og dig3. Angiv også, om partiklen accelererer eller decelererer.
Acceleration er afledt af hastighedsfunktionen, derfor svarer det til hældningen af tangentlinien til kurven v (t) i et givet øjeblik t.
For øjeblikket t1, hældningen er negativ, så accelerationen er negativ. Og da hastigheden på det øjeblik er positiv, kan vi bekræfte, at partiklen i det øjeblik aftager.
For øjeblikket tto tangentlinjen til kurven v (t) er vandret, så dens hældning er nul. Mobilen har nul acceleration, derfor ved tto partiklen accelererer eller decelererer hverken.
For øjeblikket t3, hældningen af tangentlinjen til kurven v (t) er positiv. Med en positiv acceleration accelererer partiklen virkelig, for i det øjeblik er hastigheden også positiv.
I det foregående afsnit blev øjeblikkelig acceleration defineret ud fra øjeblikkelig hastighed. Med andre ord, hvis hastigheden er kendt i hvert øjeblik, er det også muligt at kende accelerationen på hvert øjeblik af bevægelsen..
Den omvendte proces er mulig. Det vil sige at kende accelerationen for hvert øjeblik, så kan den øjeblikkelige hastighed beregnes.
Hvis den operation, der tillader at gå fra hastighed til acceleration, er afledt, er den modsatte matematiske operation integration.
Accelerationen af en partikel, der bevæger sig langs X-aksen, er a (t) = ¼ tto. Hvor t måles i sekunder og a i m / s. Bestem accelerationen og hastigheden af partiklen ved 2 s bevægelse, idet du ved, at det første øjeblik t0 = 0 var i ro.
Ved 2 s er accelerationen 1 m / sto og hastigheden for øjeblikket t vil blive givet af:
Et objekt bevæger sig langs X-aksen med en hastighed i m / s, givet af:
v (t) = 3 tto - 2 t, hvor t måles i sekunder. Bestem accelerationen til tider: 0s, 1s, 3s.
Ved at tage afledningen af v (t) med hensyn til t opnås accelerationen på ethvert tidspunkt:
a (t) = 6t -2
Derefter er (0) = -2 m / sto ; a (1) = 4 m / sto ; a (3) = 16 m / sto .
En metalkugle frigøres fra toppen af en bygning. Faldende acceleration er tyngdeacceleration, der kan tilnærmes med værdien 10 m / s2 og peger nedad. Bestem kuglens hastighed 3 s, efter at den er blevet frigivet.
Dette problem indebærer acceleration af tyngdekraften. At tage den lodrette retning som positiv ned, vi har, at sfærens acceleration er:
a (t) = 10 m / sto
Og hastigheden vil blive givet af:
En metalkugle skyder opad med en indledende hastighed på 30 m / s. Bevægelsesacceleration er tyngdeacceleration, som kan tilnærmes med værdien 10 m / sto og peger nedad. Bestem kuglens hastighed ved 2 s og 4 s, efter at den er blevet skudt.
Den lodrette retning tages som positiv opad. OGI så fald vil accelerationen af bevægelsen blive givet af
a (t) = -10 m / sto
Hastigheden som en funktion af tiden vil blive givet af:
Efter at 4 s er blevet fyret, vil hastigheden være 30 - 10 ∙ 4 = -10 m / s. Hvilket betyder, at kuglen ved 4 s er faldende med en hastighed på 10 m / s.
Endnu ingen kommentarer