
Mesh analyse begreber, metoder, eksempler
Det mesh analyse er en teknik, der bruges til at løse flade elektriske kredsløb. Denne procedure kan også forekomme i litteraturen under metodens navne på kredsløbsstrømme eller metode til netstrømme (eller løkke).
Grundlaget for denne og andre metoder til analyse af elektriske kredsløb er i Kirchhoffs love og Ohms lov. Kirchhoffs love er til gengæld udtryk for to meget vigtige principper for bevarelse i fysik for isolerede systemer: både den elektriske ladning og energien er bevaret..

På den ene side er den elektriske ladning relateret til strømmen, hvilket er ladningen i bevægelse, mens i et kredsløb er energien forbundet med spændingen, som er den agent, der har ansvaret for at udføre det arbejde, der er nødvendigt for at holde opladningen inde bevægelse..
Disse love, der anvendes på et fladt kredsløb, genererer et sæt samtidige ligninger, der skal løses for at opnå strøm- eller spændingsværdierne..
Ligningssystemet kan løses med velkendte analytiske teknikker, såsom cramer's regel, der kræver beregning af determinanter for at opnå en løsning af systemet.
Afhængigt af antallet af ligninger løses de ved hjælp af en videnskabelig lommeregner eller en eller anden matematisk software. På nettet er der også mange muligheder.
Artikelindeks
- 1 Vigtige vilkår
- 2 Metoder
- 2.1 - Trin til anvendelse af mesh-analyse
- 3 Løst øvelser
- 3.1 - Eksempel 1
- 3.2 - Eksempel 2
- 4 Referencer
Vigtige vilkår
Før vi forklarer, hvordan det fungerer, begynder vi med at definere disse udtryk:
Afdeling: sektion, der indeholder et kredsløbselement.
Node: punkt, der forbinder to eller flere grene.
Bånd: er en hvilken som helst lukket del af et kredsløb, der starter og slutter ved samme knude.
Mesh: loop, der ikke indeholder nogen anden loop inde (væsentligt mesh).
Metoder
Mesh-analyse er en generel metode, der bruges til at løse kredsløb, hvis elementer er forbundet i serie, parallelt eller på en blandet måde, det vil sige når forbindelsestypen ikke skelnes klart. Kredsløbet skal være fladt, eller i det mindste skal det være muligt at tegne det igen som sådan.
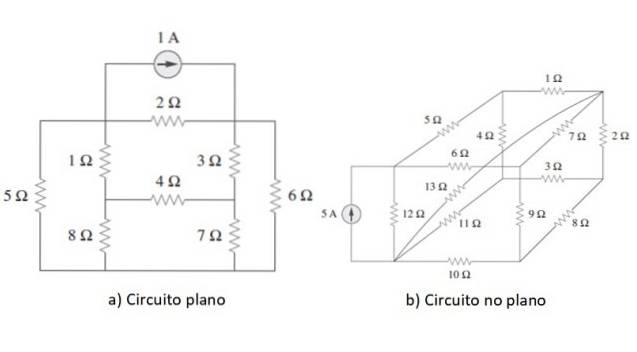
Et eksempel på hver type kredsløb er vist i figuren ovenfor. Når punktet er afklaret, vil vi begynde med at anvende metoden på et simpelt kredsløb som et eksempel i det næste afsnit, men først gennemgår vi kort lovene til Ohm og Kirchhoff.
Ohms lov: være V spændingen, R modstand e jeg strømmen af det ohmske resistive element, hvor spændingen og strømmen er direkte proportionale, hvor modstanden er proportionalitetskonstanten:
V = I.R
Kirchhoffs spændingslov (LKV): I en lukket sti, der kun køres i en retning, er den algebraiske sum af spændingerne nul. Dette inkluderer spændinger på grund af kilder, modstande, induktorer eller kondensatorer: ∑ E = ∑ Rjeg. jeg
Kirchhoffs nuværende lov (LKC): på en hvilken som helst knude er den algebraiske sum af strømme nul, idet man tager i betragtning, at de indgående strømme tildeles et tegn, og dem der forlader et andet. På denne måde: ∑ I = 0.
Med netstrømmetoden er det ikke nødvendigt at anvende Kirchhoffs nuværende lov, hvilket resulterer i færre ligninger at løse.
- Trin til anvendelse af maskeanalyse
Vi starter med at forklare metoden til et 2-mesh kredsløb. Proceduren kan derefter udvides til større kredsløb.
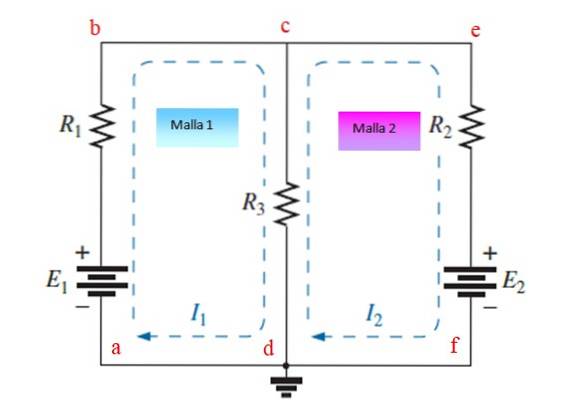
Trin 1
Tildel og tegne uafhængige strømme til hvert maske, i dette eksempel er de jeg1 og jegto. De kan tegnes med eller mod uret.
Trin 2
Anvend Kirchhoffs lov om spændinger (LTK) og Ohms lov på hvert maske. Potentielle dråber tildeles et tegn (-), mens stigninger tildeles et tegn (+).
Mesh abcda
Fra punkt a og efter strømens retning finder vi en potentiel stigning i batteri E1 (+), derefter et fald i R1 (-) og derefter endnu et fald i R3 (-).
Samtidig er modstanden R3 er også krydset af nuværende Ito, men i den modsatte retning repræsenterer det derfor en stigning (+). Den første ligning ser sådan ud:
OG1-R1.jeg1 -R3.jeg1 + R3.jegto = 0
Derefter indregnes det, og vilkårene grupperes igen:
- (R1+R3) Jeg1 +R3jegto = -E1 (Ligning 1)
Cefdc mesh
Startende fra det punkt og og efter strømens retning findes et potentielt fald i Rto (-), endnu et fald OGto, siden strømmen kommer ind gennem batteriets + pol og til sidst endnu et fald i R3 (-), På samme tid den aktuelle jeg1 krydser R3 i modsat retning (+).
Den anden ligning med de angivne tegn ser sådan ud:
- Rto jegto - OGto -R3 jegto +R3 jeg1= 0
R3jeg1 - (Rto +R3) jegto = Eto (Ligning 2)
Bemærk, at der er to ligninger med de to ukendte I1 og jegto.
Trin 3
Det således dannede ligningssystem løses derefter.
Løst øvelser
Til at begynde med er det vigtigt at overveje følgende:
-Loopstrømme eller meshstrømme kan tildeles en vilkårlig adresse.
-Hvert væsentligt maske - eller "vindue" - som kredsløbet har, skal tildeles en strøm.
-Netstrømme er betegnet med et stort bogstav for at skelne dem fra strømme, der cirkulerer gennem grene, selv om strømmen, der cirkulerer gennem en gren, i nogle tilfælde kan være den samme som netværket.
- Eksempel 1
Find de strømme, der strømmer gennem hver modstand i kredsløbet i figur 3, hvis elementerne har følgende værdier:
R1 = 20 Ω; Rto = 30 Ω; R3 = 10 Ω; OG1 = 12 V; OGto = 18 V.
Opløsning
For det første er det nødvendigt at tildele maskestrømmene I1 og jegto og tag ligningssystemet som trukket i det foregående afsnit, og erstat derefter værdierne i udsagnet:
- (R1+R3) Jeg1 +R3jegto = -E1 (Ligning 1)
R3jeg1 - (Rto +R3) jegto = Eto (Ligning 2)
-
-(20 + 30) jeg1 + 10Ito = -12
10I1 - (30 +10) Ito = 18
--
-halvtredsjeg1 + 10Ito = -12
10I1 - 40 jegto = 18
Da det er et 2 x 2 ligningssystem, kan det let løses ved reduktion, gangende den anden ligning med 5 for at eliminere det ukendte jeg1:
-halvtredsjeg1 + 10 jegto = -12
50I1 - 200 jegto = 90
-
-190 Ito= 78
jegto = - 78/180 A = - 0,41 A
Straks rydder strømmen jeg1 fra en af de originale ligninger:
jeg1 = (18 + 40 Ito) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A
Det negative tegn i strømmen jegto betyder, at strømmen i maske 2 cirkulerer i den modsatte retning af den, der er trukket.
Strømmene i hver modstand er som følger:
For modstanden R1 strømmen cirkulerer jeg1 = 0,16 A. i den forstand trukket af modstand Rto strømmen cirkulerer jegto = 0,41 A. i den modsatte retning af den, der er tegnet, og af modstanden R3 cirkulere jeg3 = 0,16- (-0,41) A = 0,57 A. ned.
Systemløsning efter Cramer's metode
I matrixform kan systemet løses som følger:
Trin 1: Beregn Δ

Trin 2: Beregn Δ1
Den første kolonne erstattes af de uafhængige vilkår i ligningssystemet, idet den opretholder den rækkefølge, som systemet oprindeligt blev foreslået:

Trin 3: Beregn I1
jeg1 = Δ1/ Δ = 300/1900 = 0,16 A
Trin 4: Beregn Δto

jegto = Δto/ Δ = -780/1900 = -0,41 A.
- Eksempel 2
Bestem strømmen og spændingerne gennem hver modstand i det følgende kredsløb ved hjælp af metoden med netstrømme:

Opløsning
De tre netstrømme er tegnet, som vist i den følgende figur, i vilkårlige retninger. Nu krydses maskerne startende fra ethvert punkt:
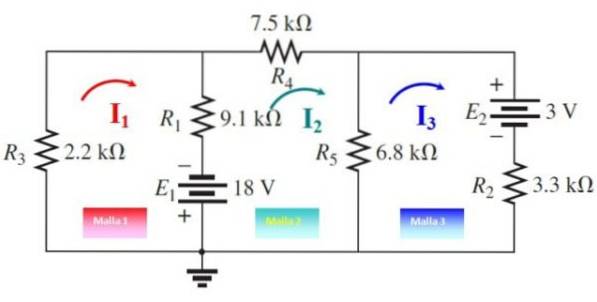
Mask 1
-9100.I1+18-2200.I1+9100.Ito= 0
-11300 I1 + 9100.Ito = -18
Mesh 2
-(7500 + 6800 + 9100) .Ito + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.Ito + 6800.I3 = 18
Mesh 3
-(6800 + 3300) I3 + 6800.Ito - 3 = 0
6800.Ito - 10100.I3 = 3
System af ligninger
-11300 I1 + 9100.Ito + 0.I3= -18
9100.I1 - 23400.Ito + 6800.I3 = 18
0.I1 + 6800.Ito - 10100.I3 = 3
Selvom antallet er stort, kan det løses hurtigt ved hjælp af en videnskabelig lommeregner. Husk, at ligningerne skal bestilles, og tilføj nuller på de steder, hvor det ukendte ikke vises, som det vises her.
Netstrømmene er:
jeg1 = 0,0012 A; jegto = -0.00048 A; jeg3 = -0.00062 A.
Strømme jegto og jeg3 cirkulere i den modsatte retning af den, der er vist i figuren, da de viste sig at være negative.
Tabel over strømme og spændinger i hver modstand
| Modstand (Ω) | Strøm (ampere) | Spænding = I.R (volt) |
|---|---|---|
| 9100 | jeg1 -jegto = 0,0012 - (- 0,00048) = 0,00168 | 15.3 |
| 3300 | 0,00062 | 2,05 |
| 2200 | 0,0012 | 2.64 |
| 7500 | 0,00048 | 3.60 |
| 6800 | jegto -jeg3= -0.00048 - (- 0.00062) = 0.00014 | 0,95 |
Cramer's regelløsning
Da det er et stort antal, er det praktisk at bruge videnskabelig notation til at arbejde direkte med dem.
Beregning af I1
De farvede pile i 3 x 3 determinanten angiver, hvordan man finder de numeriske værdier ved at gange de angivne værdier. Lad os starte med at få dem fra den første parentes i determinanten Δ:
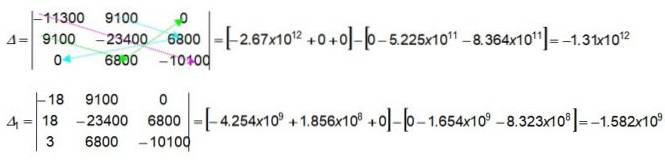
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Umiddelbart opnår vi den anden parentes i den samme determinant, som arbejdes fra venstre mod højre (for denne parentes blev de farvede pile ikke tegnet i figuren). Vi inviterer læseren til at kontrollere det:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10elleve
6800 x 6800 x (-11300) = -5,255 x 10elleve
På samme måde kan læseren også kontrollere værdierne for determinanten Δ1.
Vigtig: mellem begge parenteser er der altid et negativt tegn.
Endelig får du strømmen jeg1 igennem jeg1 = Δ1 / Δ
jeg1 = -1,582 x 109/-1,31 x 1012 = 0,0012 A.
Beregning af Ito
Proceduren kan gentages for at beregne jegto, i dette tilfælde at beregne determinanten Δto den anden kolonne i determinanten Δ erstattes af kolonnen med de uafhængige termer, og dens værdi findes ifølge den forklarede procedure.
Da det er besværligt på grund af det store antal, især hvis du ikke har en videnskabelig lommeregner, er det nemmeste at erstatte værdien af jeg1 allerede beregnet, i følgende ligning og klart:
-11300 I1 + 9100.Ito + 0.I3= -18 → 9100 Ito= -18 + 11300 I1 → Jegto = -0.00048 A.
Beregning af I3
Én gang med værdierne for jeg1 og jegto i hånden, den af jeg3 fundet direkte ved erstatning.
Referencer
- Alexander, C. 2006. Grundlæggende om elektriske kredsløb. 3. Udgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduktion til kredsløbsanalyse. 2da. Udgave. Pearson.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Volumen 5. Elektrisk interaktion. Redigeret af Douglas Figueroa (USB).
- García, L. 2014. Elektromagnetisme. 2. plads Udgave. Industrial University of Santander.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 2.



Endnu ingen kommentarer