Det fabriksrig Det er en simpel maskine, der består af et arrangement af remskiver med en multiplikationseffekt af kraften. På denne måde kan en last løftes ved at påføre lige så meget som en brøkdel af vægten på rebets frie ende..
Den består af to sæt remskiver: en, der er fastgjort til en støtte, og en anden, der udøver den resulterende kraft på lasten. Remskiverne er monteret på en generelt metallisk ramme, der holder dem.
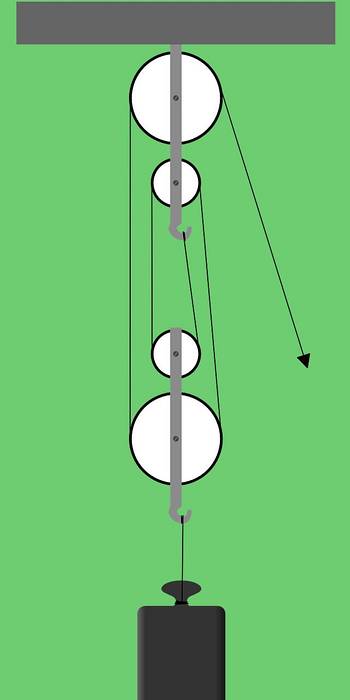
Figur 1 viser en fabriksrigg bestående af to grupper med to remskiver hver. Denne type remskiveordning kaldes også seriel rigning eller hejseværker.
Artikelindeks
For at forstå hvorfor dette arrangement multiplicerer den udøvede kraft, starter vi med det enkleste tilfælde, som består af en fast remskive og en mobil remskive..
I figur 2 har vi en remskive A fastgjort til loftet ved hjælp af en understøtning. Remskive A kan rotere frit omkring sin akse. Vi har også en remskive B, der er fastgjort til en remskive, som belastningen er placeret på. Remskive B har, ud over at være i stand til at rotere frit omkring sin akse, muligheden for at bevæge sig lodret.
Antag, at vi er i en ligevægtssituation. Overvej de kræfter, der virker på remskive B. Aksen på remskive B understøtter en totalvægt P, der er rettet nedad. Hvis dette var den eneste kraft på remskive B, ville den falde, men vi ved, at rebet, der passerer gennem denne remskive, også udøver to kræfter, som er T1 og T2, der er rettet opad..
For at der skal være translationel ligevægt, skal de to opadgående kræfter være lig med den vægt, der understøttes af remskive B.
T1 + T2 = P
Men da remskive B også er i rotationsligevægt, er T1 = T2. Kræfterne T1 og T2 kommer fra den spænding, der påføres strengen, kaldet T.
Derfor er T1 = T2 = T. Ved at erstatte i den forrige ligning forbliver den:
T + T = P
2T = P
Hvilket indikerer, at spændingen på rebet kun er halvdelen af vægten:
T = P / 2
For eksempel, hvis lasten var 100 kg, ville det være nok at anvende en kraft på 50 kg i rebets frie ende for at hæve lasten med en konstant hastighed..
Lad os nu overveje spændinger og kræfter, der virker på en samling bestående af to arrangementer af understøtninger A og B med to remskiver hver..
Støtte B har mulighed for at bevæge sig lodret, og de kræfter, der virker på den, er:
- Lastens vægt P, lodret nedad.
- To spændinger på den store remskive og to spændinger på den lille remskive. I alt fire spændinger, som alle peger opad.
For at der skal være translationel ligevægt, er det nødvendigt, at de kræfter, der peger lodret op, er lige store i værdi til belastningen, der peger nedad. Det vil sige, det skal være opfyldt:
T + T + T + T = P
Det vil sige 4 T = P
Heraf følger, at den påførte kraft T ved rebets frie ende kun er en fjerdedel af vægten på grund af den belastning, der vil løftes., T = P / 4.
Med denne værdi for spændingen T kan belastningen holdes statisk eller stige med konstant hastighed. Hvis en spænding større end denne værdi blev anvendt, ville belastningen accelere opad, en tilstand, der er nødvendig for at bringe den ud af hvile..
Ifølge det, der er set i de foregående tilfælde, er der for hver remskive i den mobile enhed et par opadgående kræfter, der udøves af rebet, der passerer gennem remskiven. Men denne kraft kan ikke være andet end den spænding, der påføres rebet i den frie ende.
Så for hver remskive i den mobile enhed vil der være en lodret opadgående kraft, der er lig med 2T. Men da der er n remskiver i den bevægelige enhed, følger det, at den samlede kraft, der peger lodret opad, er:
2 n T
For at der skal være lodret balance er det nødvendigt, at:
2 n T = P
derfor er den kraft, der påføres i den frie ende:
T = P / (2 n)
I dette tilfælde kan det siges, at den udøvede kraft T ganges 2 n gange på belastningen.
For eksempel, hvis vi havde en fabriksrigg med 3 faste og 3 mobile remskiver, ville tallet n være lig med 3. På den anden side, hvis belastningen var P = 120 kg, ville kraften, der blev anvendt i den frie ende, være T = 120 kg / (2 * 3) = 20 kg.
Overvej en faktorrig der består af to faste remskiver og to bevægelige remskiver. Den maksimale spænding, som rebet kan modstå, er 60 kg. Bestem, hvad der er den maksimale belastning, der kan placeres.
Når lasten hviler eller bevæger sig med konstant hastighed, er dens vægt P relateret til spændingen T, der påføres rebet ved hjælp af følgende forhold:
P = 2 n T
Da det er en rig med to mobile og to faste remskiver, så er n = 2.
Den maksimale belastning, der kan placeres, opnås, når T har den maksimalt mulige værdi, som i dette tilfælde er 60 kg.
Maksimal belastning = 2 * 2 * 60 kg = 240 kg
Find forholdet mellem rebspændingen og vægten af lasten i en faktorisk rig med to remskiver, hvor belastningen accelereres med acceleration ved.
Forskellen i dette eksempel med hensyn til hvad der hidtil er set er, at systemets dynamik skal overvejes. Så vi foreslår Newtons anden lov for at finde det ønskede forhold.
I figur 4 tegner vi gule kræfter på grund af rebets spænding. Hejsens bevægelige del har en total masse M. Vi tager som et referencesystem en på niveau med den første faste remskive og positiv nedad.
Y1 er den laveste remskiveposition.
Vi anvender Newtons anden lov til at bestemme accelerationen a1 for den bevægelige del af riggen:
-4 T + Mg = M al
Da belastningens vægt er P = Mg, hvor g er tyngdeacceleration, kan ovenstående forhold skrives:
-4T + P = P (al / g)
Hvis vi ønskede at bestemme spændingen på rebet, når en bestemt vægtbelastning P accelereres med acceleration a1, ville det tidligere forhold se sådan ud:
T = P (1 - al / g) / 4
Bemærk, at hvis systemet var i ro eller bevæger sig med konstant hastighed, så var a1 = 0, og vi ville genvinde det samme udtryk, som vi fik i tilfælde 2.
I dette eksempel anvendes den samme rigning fra øvelse 1 med det samme reb, der understøtter maksimalt 60 kg spænding. En bestemt belastning hæves, hvilket accelererer det fra hvile til 1 m / s på 0,5 sek. Ved hjælp af rebets maksimale spænding. Find lastens maksimale vægt.
Vi vil bruge de udtryk, der er opnået i øvelse 2, og referencesystemet i figur 4, hvor den positive retning er lodret nedad.
Belastningens acceleration er a1 = (-1 m / s - 0 m / s) / 0,5 s = -2 m / s ^ 2.
Vægten af belastningen i kilo-kraft er angivet ved
P = 4 T / (1 - al / g)
P = 4 * 60 kg / (1 + 2 / 9,8) = 199,3 kg
Dette er den maksimalt mulige vægt af lasten uden rebet går i stykker. Bemærk, at den opnåede værdi er mindre end den, der er opnået i eksempel 1, hvor belastningen blev antaget at have nul acceleration, dvs. i hvile eller med konstant hastighed..
Endnu ingen kommentarer