
Aksial belastning, hvordan den beregnes og øvelser løses
Det aksial belastning Det er den kraft, der er rettet parallelt med et elements symmetriakse, der udgør en struktur. Den aksiale kraft eller belastning kan være spænding eller kompression. Hvis aksialkraftens handlingslinje falder sammen med symmetriaksen, der passerer gennem centret af det betragtede element, siges det at være en koncentrisk aksial belastning eller kraft.
Tværtimod, hvis det er en aksial kraft eller belastning parallelt med symmetriaksen, men hvis handlingslinje ikke er på selve aksen, er det en excentrisk aksial kraft.
-
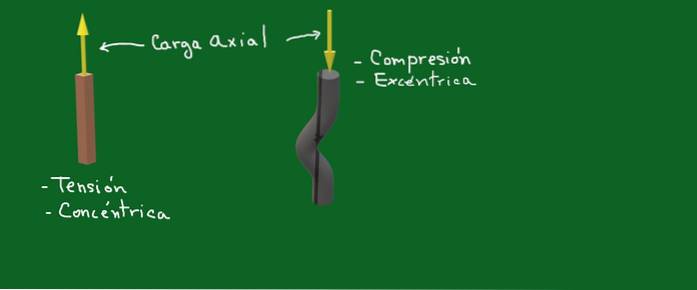
Figur 1. Aksial belastning. Kilde: selvfremstillet
I figur 1 repræsenterer de gule pile aksiale kræfter eller belastninger. I det ene tilfælde er det en koncentrisk spændingskraft, og i det andet har vi en excentrisk kompressionskraft at gøre.
Måleenheden for aksial belastning i det internationale SI-system er Newton (N). Men andre kraftenheder såsom kilogram-kraft (kg-f) og pund-kraft (lb-f) bruges også ofte..
Artikelindeks
- 1 Hvordan beregnes det?
- 1.1 Forholdet mellem aksial belastning og normal belastning
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 3 Referencer
Hvordan beregnes det?
For at beregne værdien af den aksiale belastning i elementerne i en struktur skal følgende trin følges:
- Lav kraftdiagrammet for hvert element.
- Anvend ligningerne, der garanterer translationel ligevægt, det vil sige, at summen af alle kræfter er nul.
- Overvej ligningen af drejningsmomenter eller øjeblikke, så rotationsligevægt er opfyldt. I dette tilfælde skal summen af alle drejningsmomenter være nul.
- Beregn kræfterne samt identificer kræfterne eller aksialbelastningen i hvert af elementerne.
Forholdet mellem aksial belastning og normal belastning
Gennemsnitlig normal belastning defineres som forholdet mellem aksial belastning divideret med tværsnitsareal. Enhederne til normal indsats i International System S.I. de er Newton over kvadratmeter (N / m²) eller Pascal (Pa). Følgende figur 2 illustrerer begrebet normal stress for klarhedens skyld..
-
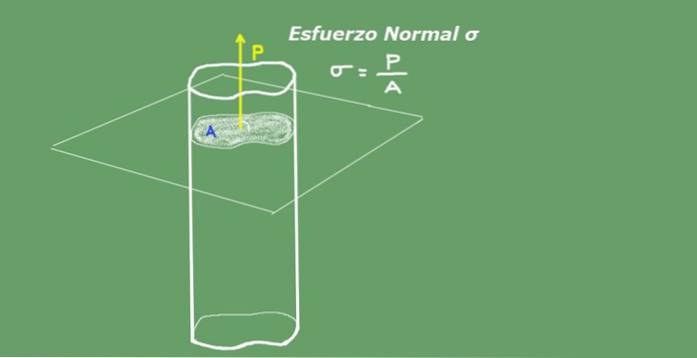
Figur 2. Normal stress. Kilde: selvfremstillet.
Løst øvelser
-Øvelse 1
Overvej en cylindrisk betonsøjle med højde h og radius r. Antag, at densiteten af beton er ρ. Søjlen understøtter ikke yderligere ekstra belastning end sin egen vægt og understøttes på en rektangulær base.
- Find værdien af den aksiale belastning ved punkterne A, B, C og D, som er i følgende positioner: A i bunden af søjlen, B a ⅓ i højden h, C a ⅔ i højden h og sidste D ved øverst i søjlen.
- Bestem også den gennemsnitlige normale stress ved hver af disse positioner. Tag følgende numeriske værdier: h = 3m, r = 20cm og ρ = 2250 kg / m³
-
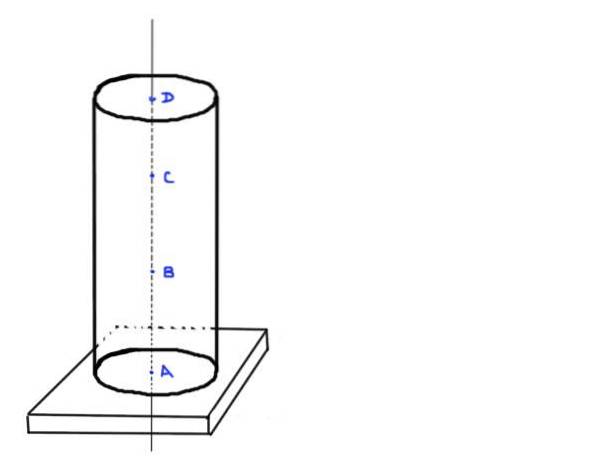
Figur 3. Cylindrisk søjle. Kilde: selvfremstillet.
Opløsning
Samlet kolonnevægt
Kolonnens samlede vægt W er produktet af dens densitet gange volumen ganget med tyngdeacceleration:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Aksial belastning i A
Ved punkt A skal søjlen understøtte sin fulde vægt, så den aksiale belastning på dette tidspunkt er kompression er lig med søjlens vægt:
PA = W = 8313 N
Aksial belastning ved B
Kun ⅔ af søjlen vil være på punkt B, så den aksiale belastning på dette punkt vil være kompression og dens værdi ⅔ søjlens vægt:
PB = ⅔ W = 5542 N
Figur 3. Cylindrisk søjle. Kilde: selvfremstillet.
Over position C er der kun ⅓ i søjlen, så dens aksiale kompressionsbelastning vil være ⅓ med sin egen vægt:
PC = ⅓ W = 2771 N
Aksial belastning i D
Endelig er der ingen belastning på punkt D, som er den øverste ende af søjlen, så den aksiale kraft på dette punkt er nul..
PD = 0 N
Normal indsats i hver af stillingerne
For at bestemme den normale spænding i hver af positionerne er det nødvendigt at beregne tværsnittet af område A, som er givet ved:
A = π ∙ r² = 0,126 m²
På denne måde vil den normale spænding i hver af positionerne være kvotienten mellem den aksiale kraft i hvert af punkterne divideret med det allerede beregnede tværsnitsareal, hvilket i denne øvelse er det samme for alle punkterne, fordi det er en søjle cylindrisk.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Øvelse 2
Figuren viser en struktur, der består af to søjler, som vi vil kalde AB og CB. Stang AB understøttes i enden A af en stift og i den anden ende er forbundet til den anden stang af en anden stift B.
Tilsvarende understøttes stangen CB i enden C ved hjælp af en stift og i enden B med stiften B, der forbinder den med den anden stang. En lodret kraft eller belastning F påføres pin B som vist i følgende figur:
-
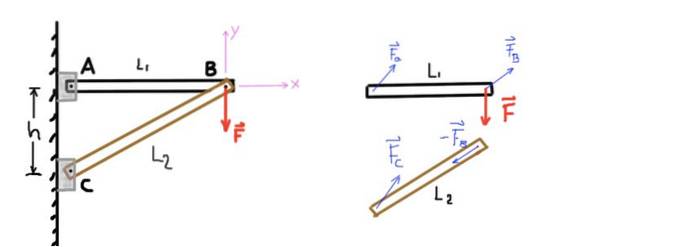
Figur 4. To-bjælkes struktur og frit kropsdiagram. Kilde: selvfremstillet.
Antag, at stængernes vægt er ubetydelig, da kraften F = 500 kg-f er meget større end vægten af strukturen. Adskillelsen mellem understøtninger A og C er h = 1,5 m, og længden af stangen AB er L1 = 2 m. Bestem den aksiale belastning på hver af bjælkerne, og angiv, om det er kompression eller aksial belastning.
Løsning 2
Figuren viser ved hjælp af et frit legemsdiagram de kræfter, der virker på hvert af elementerne i strukturen. Det kartesiske koordinatsystem, hvormed styrkeligevægtsligningerne etableres, er også angivet..
Moment eller øjeblikke beregnes ved punkt B og betragtes som positive, hvis de peger væk fra skærmen (Z-aksen). Balancen mellem kræfter og drejningsmomenter for hver søjle er:
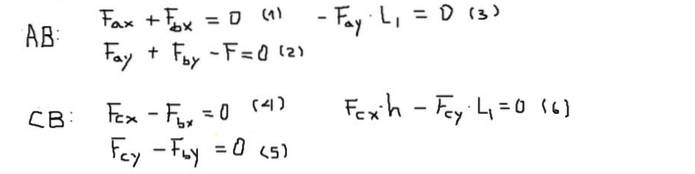
Dernæst løses komponenterne i kræfterne i hver af ligningerne i følgende rækkefølge:
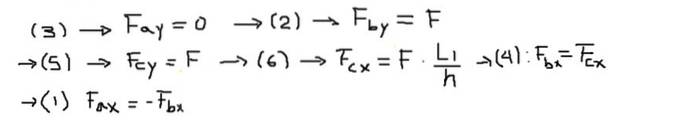
Endelig beregnes de resulterende kræfter i enderne af hver bjælke:
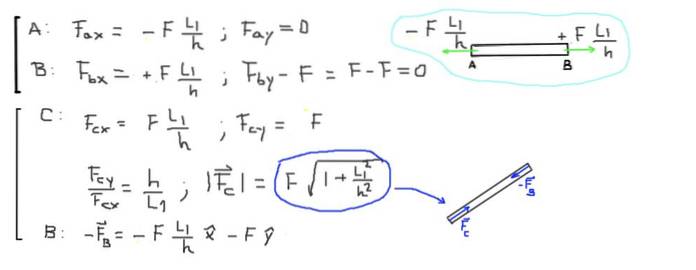
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
Stangen CB er i kompression på grund af de to kræfter, der virker ved dens ender, der er parallelle med stangen og peger mod dens centrum. Størrelsen af den aksiale kompressionskraft i bjælken CB er:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Referencer
- Øl F ... Mekanik af materialer. 5. plads Udgave. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Mekanik af materialer. Ottende udgave. Prentice Hall. 2011. 3-60.
- Gere J. Mekanik af materialer. Ottende udgave. Cengage læring. 4-220.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. udgave Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Noter om generel fysik. UNAM. 87-98.


Endnu ingen kommentarer