Det effektiv nuklear afgift (Zef) er den tiltrækkende kraft, som kernen udøver på nogen af elektronerne efter at være blevet reduceret af virkningerne af afskærmning og penetration. Hvis der ikke var sådanne effekter, ville elektronerne føle den attraktive kraft af den virkelige nukleare ladning Z.
På billedet nedenfor har vi Bohr-atommodellen for et fiktivt atom. Dens kerne har en nuklear ladning Z = + n, som tiltrækker de elektroner, der kredser omkring den (de blå cirkler). Det kan ses, at to elektroner befinder sig i en kredsløb tættere på kernen, mens den tredje elektron ligger i større afstand fra den..
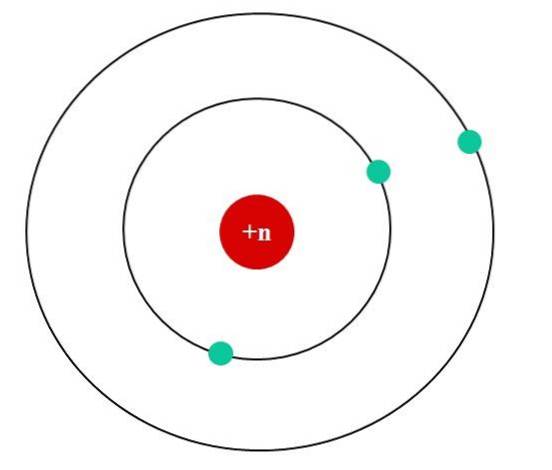
Den tredje elektron kredser om følelsen af de elektrostatiske frastød fra de to andre elektroner, så kernen tiltrækker den med mindre kraft; det vil sige, at kerne-elektron-interaktionen aftager som et resultat af afskærmningen af de to første elektroner.
Så de første to elektroner føler den attraktive kraft af en + n-ladning, men den tredje oplever en effektiv nuklear ladning på + (n-2) i stedet..
Imidlertid sagde Zef kun gyldigt, hvis afstandene (radius) til kernen på alle elektroner altid var konstante og bestemte og lokaliserede deres negative ladninger (-1).
Artikelindeks
Protoner definerer kernerne af kemiske grundstoffer, og elektroner definerer deres identitet inden for et sæt karakteristika (grupperne i det periodiske system)..
Protoner øger den nukleare ladning Z med hastigheden n + 1, hvilket kompenseres ved tilsætning af en ny elektron for at stabilisere atomet.
Efterhånden som antallet af protoner stiger, er kernen "dækket" af en dynamisk sky af elektroner, hvor de regioner, gennem hvilke de cirkulerer, er defineret af sandsynlighedsfordelingerne af de radiale og vinklede dele af bølgefunktionerne (orbitalerne).
Fra denne tilgang kredser elektronerne ikke i et defineret område af rummet omkring kernen, men snarere, som bladene på en hurtigt roterende blæser, sløres de ud i formen af de kendte orbitaler s, p, d og f.
Af denne grund fordeles den elektroniske ladning -1 af en elektron af de regioner, som orbitalerne trænger igennem; jo større den gennemtrængende virkning er, desto større er den effektive nukleare ladning, som elektronen oplever i kredsløbet.
Ifølge forklaringen ovenfor bidrager elektronerne i de indre skaller ikke med en -1 ladning til den stabiliserende frastødning af elektronerne i de ydre skaller..
Imidlertid tjener denne kerne (skaller, der tidligere er fyldt med elektroner) som en "væg", der forhindrer den attraktive kraft af kernen i at nå de ydre elektroner..
Dette er kendt som skærmeffekten eller afskærmningseffekten. Desuden oplever ikke alle elektronerne i de ydre skaller den samme størrelse af denne effekt; for eksempel, hvis du besætter en orbital, der har en høj gennemtrængende karakter (det vil sige, der passerer meget tæt på kernen og andre orbitaler), så vil du føle en højere Zef.
Som et resultat opstår en rækkefølge af energisk stabilitet som en funktion af disse Zef for orbitalerne: s Dette betyder, at 2p-orbitalen har højere energi (mindre stabiliseret af kerneens ladning) end 2s-orbitalen.. Jo dårligere penetreringseffekten udøves af orbitalen, jo mindre vil dens afskærmende virkning have på resten af de eksterne elektroner. D- og f-orbitalerne viser mange huller (noder), hvor kernen tiltrækker andre elektroner. Forudsat at de negative ladninger er lokaliserede, er formlen til beregning af Zef for enhver elektron: Zef = Z - σ I denne formel er σ afskærmningskonstanten bestemt af kernerne. Dette skyldes, at de yderste elektroner teoretisk ikke bidrager til afskærmningen af de indre elektroner. Med andre ord, 1sto skjoldelektron 2s1, men 2s1 beskytter ikke Z-elektroner 1sto. Hvis Z = 40, forsømmelse af de nævnte effekter, vil den sidste elektron opleve en Zef lig med 1 (40-39). Slaters regel er en god tilnærmelse af Zef-værdierne for elektronerne i atomet. Følg nedenstående trin for at anvende det: 1- Den elektroniske konfiguration af atomet (eller ionen) skal skrives som følger: (1s) (2s 2p) (3s 3p) (3d) (4s 4p) (4d) (4f) ... 2- De elektroner, der er til højre for den, der overvejes, bidrager ikke til afskærmningseffekten. 3- Elektronerne, der er inden for den samme gruppe (markeret med parenteser) tilvejebringer 0,35 ladningen af elektronen, medmindre det er 1s-gruppen og er 0,30 i stedet for. 4- Hvis elektronen optager en s- eller p-orbital, bidrager alle n-1-orbitaler med 0,85, og alle n-2-orbitaler en enhed. 5- Hvis elektronen indtager en d- eller f-orbital, bidrager alle dem til venstre med en enhed. Efter Slaters repræsentationsmetode er den elektroniske konfiguration af Be (Z = 4): (1sto) (2sto2 s0) Da der er to elektroner i kredsløbet, bidrager en af disse til afskærmningen af den anden, og 1-orbitalen er n-1 af 2-orbitalen. Derefter udvikler vi den algebraiske sum: (0,35) (1) + (0,85) (2) = 2,05 0,35 kom fra 2s elektronen og 0,85 fra de to 1s elektroner. Brug nu Zefs formel: Zef = 4 - 2,05 = 1,95 Hvad betyder det? Det betyder, at elektronerne i 2s orbitalto opleve en +1,95 opladning, der trækker dem mod kernen snarere end den faktiske +4 opladning. Igen fortsætter det som i det foregående eksempel: (1sto) (2sto2 s6) (3sto3p3) Nu er den algebraiske sum udviklet til at bestemme σ: (, 35) (4) + (0,85) (8) + (1) (2) = 10,2 Så Zef er forskellen mellem σ og Z: Zef = 15-10,2 = 4,8 Afslutningsvis de sidste 3p elektroner3 de oplever en belastning tre gange mindre end den rigtige. Det skal også bemærkes, at ifølge denne regel er 3s elektronerto opleve den samme Zef, et resultat, der kunne skabe tvivl om det. Der er dog ændringer af Slaters regel, der hjælper med at tilnærme de beregnede værdier for de faktiske..Sådan beregnes det?
Slaters regel
Eksempler
Bestem Zef for elektronerne i 2s orbitalto i beryllium
Bestem Zef for elektronerne i 3p orbitalen3 af fosfor
Referencer
Endnu ingen kommentarer