
Radial belastning, hvordan man beregner det, løste øvelser
Det radial belastning Det er den kraft, der udøves vinkelret på et objekts symmetriakse, og hvis handlingslinje passerer gennem denne akse. For eksempel påfører et rem på en remskive en radial belastning på lejet eller lejet på remskiveakslen..
I figur 1 repræsenterer de gule pile radiale kræfter eller belastninger på akslerne på grund af spændingen i remmen, der passerer gennem remskiverne.
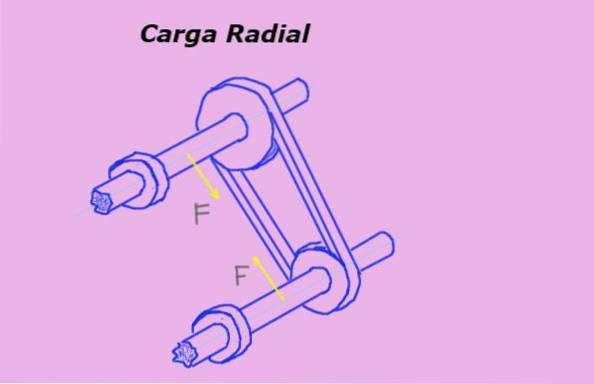
Måleenheden for radial belastning i det internationale system eller SI-systemet er Newton (N). Men andre kraftenheder bruges ofte til at måle det, såsom kilokraften (Kg-f) og pundkraften (lb-f).
Artikelindeks
- 1 Hvordan beregnes det?
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2 Øvelse 2
- 3 Referencer
Hvordan beregnes det?
For at beregne værdien af den radiale belastning på elementerne i en struktur skal følgende trin følges:
- Lav et diagram over kræfter på hvert element.
- Anvende ligningerne, der garanterer translationel ligevægt; det vil sige, at summen af alle kræfter er nul.
- Overvej ligningen af drejningsmomenter eller øjeblikke, så rotationsligevægt er opfyldt. I dette tilfælde skal summen af alle drejningsmomenter være nul.
- Beregn kræfterne for at kunne identificere de radiale belastninger, der virker på hvert af elementerne.
Løst øvelser
-Øvelse 1
Følgende figur viser en remskive, gennem hvilken en spændet remskive passerer med spænding T. Remskiven er monteret på en aksel understøttet af to lejer. Midten af en af dem er i en afstand L.1 fra midten af remskiven. I den anden ende er den anden leje, på afstand Lto.
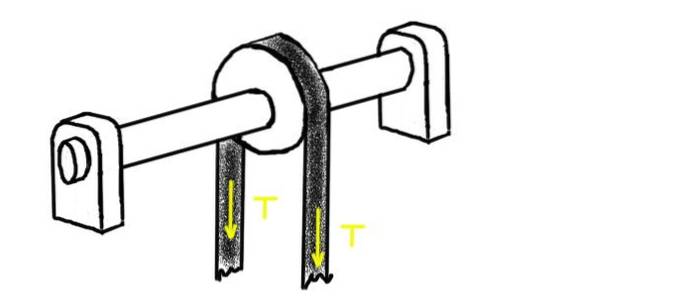
Bestem den radiale belastning på hver af lejerne, forudsat at vægten af akslen og remskiven er betydeligt mindre end den påførte spænding.
Tag som værdi for bæltespændingen 100 kg-f og for afstande L1= 1 m og L.to= 2 m.
Opløsning
Først laves der et diagram over de kræfter, der virker på aksen.
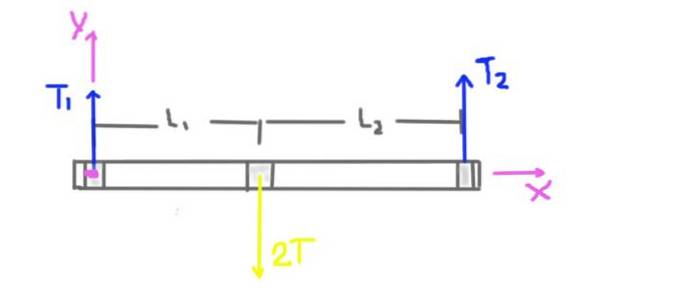
Remskivens spænding er T, men den radiale belastning på akslen ved remskivepositionen er 2T. Skaftens og remskivens vægt tages ikke i betragtning, fordi opgørelsen af problemet fortæller os, at den er betydeligt mindre end spændingen på bæltet.
Den radiale reaktion af understøtningerne på akslen er forårsaget af de radiale kræfter eller belastninger T1 og T2. Afstandene L1 og L2 fra understøtningerne til midten af remskiven er også angivet i diagrammet..
Koordinatsystemet vises også. Drejningsmomentet eller det samlede øjeblik på aksen beregnes under hensyntagen til centrum for koordinatsystemets oprindelse og vil være positivt i Z-retning.
Ligevægtsbetingelser
Nu er ligevægtsbetingelserne etableret: summen af kræfter er lig med nul og summen af moment er lig med nul.
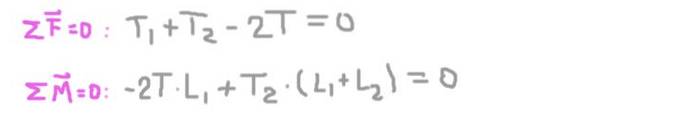
Fra den anden ligning opnår vi den radiale reaktion på aksen i understøtningen 2 (Tto), der erstatter den første og løser den radiale reaktion på aksen ved understøtning 1 (T1).
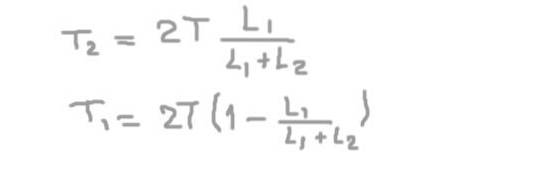
T1= (2/3) T = 66,6 kg-f
Og den radiale belastning på akslen i positionen af understøtningen 2 er:
Tto= (4/3) T = 133,3 kg-f.
Øvelse 2
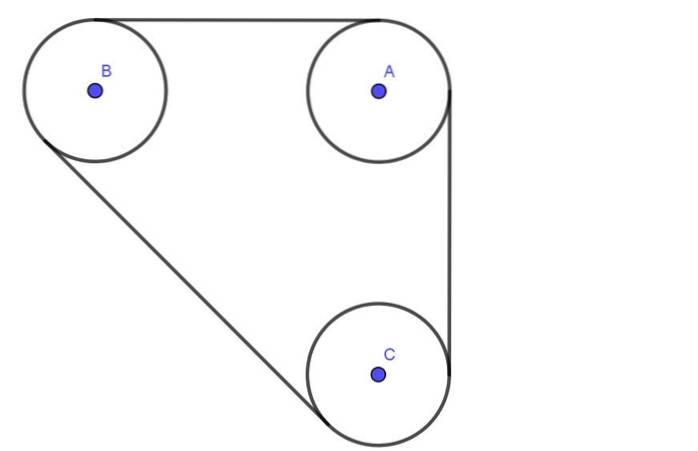
Følgende figur viser et system, der består af tre remskiver A, B, C alle med samme radius R. Remskiverne er forbundet med et bælte, der har en spænding T.
Aksler A, B, C går gennem smurte lejer. Adskillelsen mellem centrum af akser A og B er 4 gange radien R. Ligeledes er adskillelsen mellem akser B og C også 4R.
Bestem den radiale belastning på akserne på remskiverne A og B, forudsat at bæltespændingen er 600N.
Opløsning
Vi begynder med at tegne et diagram over de kræfter, der virker på remskive A og B. På den første har vi de to spændinger T1 og Tto, såvel som kraften FTIL at lejet udøver på remskivens akse A.
På remskive B har vi ligeledes spændingerne T3 , T4 og kraften FB at lejet udøver på samme akses akse. Den radiale belastning på remskive A's akse er kraften FTIL og den radiale belastning på B er kraften F.B.
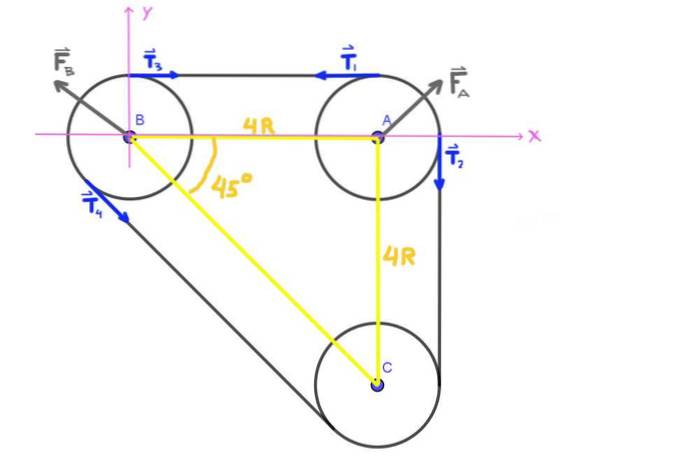
Da akserne A, B, C danner en isorektangel-trekant, er vinklen ABC 45 °.
Alle spændinger T1 , Tto , T3 , T4 vist i figuren har samme modul T, som er bæltespændingen.
Balancetilstand for remskive A
Nu skriver vi ligevægtsbetingelsen for remskive A, som ikke er andet end summen af alle de kræfter, der virker på remskive A, skal være nul.
Separering af X- og Y-komponenterne i kræfterne og tilføjelse (vektorielt) af følgende par skalære ligninger opnås:
FTILx - T = 0; FTILY - T = 0
Disse ligninger fører til følgende ligestilling: FØKSE = FOH = T.
Derfor har den radiale belastning størrelsen givet ved:
FTIL = (T² + T²)1/2 = 21/2∙ T = 1,41 ∙ T = 848,5 N. med 45 ° retning.
Balancetilstand for remskive B
På samme måde skriver vi ligevægtsbetingelsen for remskive B. For komponent X har vi: FBx + T + T ∙ Cos45 ° = 0
Y for komponent Y: FBY + T ∙ Sen45 ° = 0
Dermed:
FBX = - T (1 + 2-1/2) og FVED = -T ∙ 2-1/2
Det vil sige, størrelsen af den radiale belastning på remskive B er:
FB = ((1 + 2-1/2) ² + 2-1)1/2∙ T = 1,85 ∙ T = 1108,66 N og dens retning er 135 °.
Referencer
- Beer F, Johnston E, DeWolf J, Mazurek, D. Materialemekanik. Femte udgave. 2010. Mc Graw Hill. 1-130.
- Gere J, Goodno, B. Materialemekanik. Ottende udgave. Cengage læring. 4-220.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler R. Mekanik af materialer. Ottende udgave. Prentice Hall. 2011. 3-60.
- Valera Negrete, J. 2005. Noter om generel fysik. UNAM. 87-98.


Endnu ingen kommentarer