
Uelastisk nedbrud i en dimension og eksempler
Det uelastiske stød eller uelastiske kollisioner er en kort og intens interaktion mellem to objekter, hvor momentumet er bevaret, men ikke den kinetiske energi, hvoraf en procentdel omdannes til en anden type energi.
Nedbrud eller kollisioner er hyppige i naturen. Subatomære partikler kolliderer ved ekstremt høje hastigheder, mens mange sportsgrene og spil består af kontinuerlige kollisioner. Selv galakser er i stand til at kollidere.

I virkeligheden bevares momentum i enhver form for kollision, så længe de kolliderende partikler danner et isoleret system. Så i denne forstand er der ikke noget problem. Nu har objekter kinetisk energi forbundet med den bevægelse, de har. Hvad kan der ske med den energi, når du kolliderer??
De interne kræfter, der finder sted under kollisionen mellem objekter, er stærke. Når det anføres, at kinetisk energi ikke bevares, betyder det, at den omdannes til andre energityper: for eksempel til lydenergi (en spektakulær kollision har en særprægende lyd).
Flere anvendelsesmuligheder for kinetisk energi: friktionsvarme og selvfølgelig den uundgåelige deformation, som genstande gennemgår, når de kolliderer, såsom bilernes kroppe i figuren ovenfor.
Artikelindeks
- 1 Eksempler på uelastiske kollisioner
- 2 Perfekt uelastiske kollisioner i en dimension
- 3 Restitutionskoefficient
- 4 Sådan bestemmes restitutionskoefficienten?
- 5 arbejdede eksempler
- 5.1-Øvelse 1
- 5.2-Øvelse 2
- 5.3-Øvelse 3
- 6 Referencer
Eksempler på uelastiske kollisioner
- To masser af plasticine kolliderer og klæber sammen, bevæger sig som et stykke efter kollisionen.
- En gummikugle, der hopper af en væg eller et gulv. Bolden deformeres, når den rammer overfladen.
Ikke al kinetisk energi omdannes til andre energityper med få undtagelser. Objekter kan beholde en vis mængde af denne energi. Senere vil vi se, hvordan man beregner procentdelen.
Når kolliderende stykker holder sammen, kaldes kollisionen perfekt uelastisk, og begge har en tendens til at bevæge sig sammen..
Perfekt uelastiske kollisioner i en dimension
Kollisionen i figuren viser to objekter med forskellige masser m1 Y mto, bevæger sig mod hinanden med hastigheder vi1 Y vi2 henholdsvis. Alt sker på det vandrette, det vil sige, det er en kollision i en dimension, den nemmeste at studere.
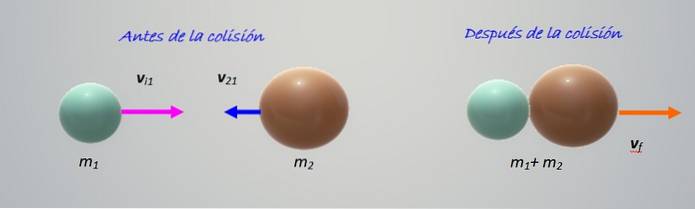
Objekterne kolliderer og klæber sig derefter sammen ved at flytte til højre. Det er en perfekt uelastisk kollision, så vi skal bare holde momentum:
Peller = PF
Momentum er en vektor, hvis SI-enheder er N.s. I den beskrevne situation kan vektornotationen udelades, når der behandles kollisioner i en dimension:
mveller = mvF
Systemets momentum er vektorsummen af hver partikels momentum.
m1 vi1 + mto vi2 = (m1 + mto) vF
Den endelige hastighed er givet af:
vF = (m1 vi1 + mto vi2) / (m1 + mto)
Restitutionskoefficient
Der er en mængde, der kan indikere, hvor elastisk en kollision er. Det handler om restitutionskoefficient, som er defineret som den negative kvotient mellem den relative hastighed af partiklerne efter kollisionen og den relative hastighed før kollisionen.
Lad os1 og digto de respektive hastigheder af partiklerne oprindeligt. Og vær v1 og Vto de respektive sluthastigheder. Matematisk kan restitutionskoefficienten udtrykkes som følger:
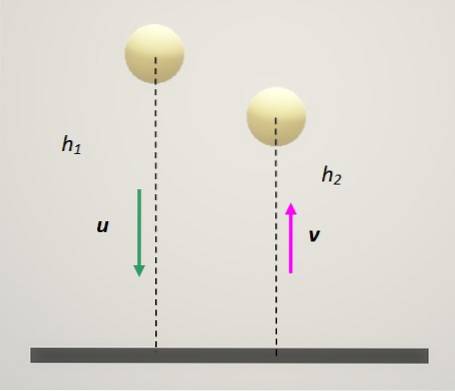
- Hvis ε = 0 svarer det til at bekræfte, at vto = v1. Det betyder, at de endelige hastigheder er de samme, og kollisionen er uelastisk, som den, der blev beskrevet i det foregående afsnit..
- Når ε = 1 betyder det, at de relative hastigheder både før og efter kollisionen ikke ændres, i dette tilfælde er kollisionen elastisk.
- Og hvis 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.
Sådan bestemmes restitutionskoefficienten?
Restitutionskoefficienten afhænger af den klasse af materialer, der er involveret i kollisionen. En meget interessant test for at bestemme, hvor elastisk et materiale er til at lave kugler, er at droppe kuglen på en fast overflade og måle reboundhøjden.

I dette tilfælde har den faste plade altid hastighed 0. Hvis den tildeles indeks 1, og kugleindekset 2 er:
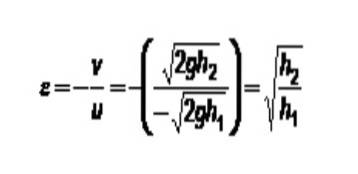



I begyndelsen er det blevet foreslået, at al kinetisk energi kan omdannes til andre energityper. Når alt kommer til alt er energi ikke ødelagt. Er det muligt, at bevægelige objekter kolliderer og forenes for at danne et enkelt objekt, der pludselig kommer til hvile? Dette er ikke så let at forestille sig.
Lad os dog forestille os, at det sker omvendt, som i en film set omvendt. Så objektet var oprindeligt i ro og eksploderede derefter, fragmenteret i forskellige dele. Denne situation er fuldt ud mulig: den er en eksplosion.
Så en eksplosion kan betragtes som en perfekt uelastisk kollision set tilbage i tiden. Momentumet er også bevaret, og det kan siges, at:
Peller = PF
Arbejdede eksempler
-Øvelse 1
Det er kendt fra målingerne, at restitutionskoefficienten for stål er 0,90. En stålkugle falder fra en højde på 7 m på en fast plade. Beregn:
a) Hvor høj vil den hoppe.
b) Hvor lang tid tager det mellem den første kontakt med overfladen og den anden.
Opløsning
a) Ligningen, der blev udledt tidligere i afsnittet om bestemmelse af restitutionskoefficienten, anvendes:
Højden er ryddet hto:
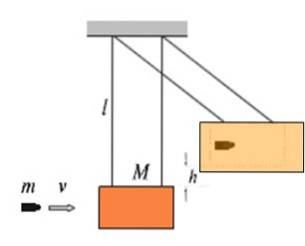
0,90to . 7 m = 5,67 m
b) For at den skal stige 5,67 meter kræves en hastighed givet af:


t maks = veller/ g = (10,54 / 9,8 s) = 1,08 s.
Den tid, det tager at vende tilbage, er den samme, derfor er den samlede tid til at klatre 5,67 meter og vende tilbage til startpunktet dobbelt så lang tid:
tflyvningen = 2,15 s.
-Øvelse 2
Figuren viser en træblok af masse M, der hænger i hvile ved strengene i længden l som et pendul. Dette kaldes et ballistisk pendul og bruges til at måle hastigheden v for indgangen til en kugle med masse m. Jo højere hastighed hvormed kuglen rammer blokken, jo højere h vil den stige.
Kuglen i billedet er indlejret i blokken, derfor er det et totalt uelastisk chok.

Antag, at en 9,72-g kugle rammer massen med en masse på 4,60 kg, så stiger samlingen 16,8 cm fra ligevægt. Hvad er hastigheden v fra kuglen?
Opløsning
Under kollisionen bevares momentum og ellerF er helhedens hastighed, når kuglen har indlejret sig i blokken:
Peller = PF
Blokken er oprindeligt i ro, mens kuglen er rettet mod målet med hastighed v:
m.v + M.0 = (m + M) uF
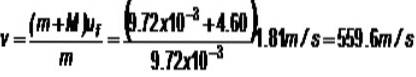
Ikke kendt ellerF stadig, men efter kollisionen bevares den mekaniske energi, dette er summen af tyngdepotentialenergien U og den kinetiske energi K:
Indledende mekanisk energi = Endelig mekanisk energi
OGmo = Emf
ELLEReller + Keller = UF + KF
Gravitationspotentiel energi afhænger af den højde, som sættet når. For ligevægtspositionen er den indledende højde den, der tages som referenceniveau, derfor:
ELLEReller = 0
Takket være kuglen har hele kinetisk energi Keller, som omdannes til tyngdepotentialenergi, når sættet når sin maksimale højde h. Den kinetiske energi er givet ved:
K = ½ mvto
Oprindeligt er den kinetiske energi:
Keller = (1/2) (M + m) uFto
Husk, at kuglen og blokken allerede danner et enkelt masseobjekt M + m. Gravitationspotentiel energi, når de har nået deres maksimale højde, er:
ELLERF = (m + M) gh
Derfor:
Keller = UF
(1/2) (M + m) uFto = (m + M) gh
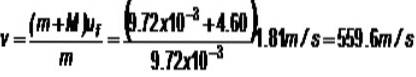
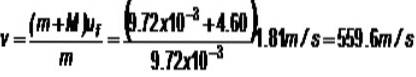
-Øvelse 3
Objektet i figuren eksploderer i tre fragmenter: to med samme masse m og en større med masse 2m. Figuren viser hastighederne på hvert fragment efter eksplosionen. Hvad var objektets starthastighed?
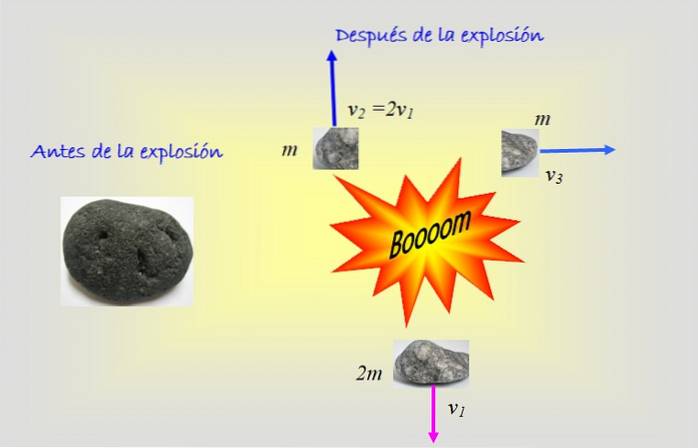
Opløsning
I dette problem kræves brugen af to koordinater: x og Y, fordi to af fragmenterne har lodrette hastigheder, mens resten har vandret hastighed.
Objektets samlede masse er summen af massen af alle fragmenter:
M = m + m + 2m = 4m
Momentet er bevaret både i x-aksen og i y-aksen, det er angivet separat:
- 4m. ellerx= m v3
- 4m. ellerY = m. 2v1 - 2m. v1
Bemærk, at det store fragment bevæger sig ned med hastighed v1, for at indikere dette faktum er der anbragt et negativt tegn på det.
Fra den anden ligning følger det straks, at ellerY = 0, og fra den første ryddes ux med det samme:

Referencer
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6th. Ed Prentice Hall. 175-181
- Rex, A. 2011. Grundlæggende fysik. Pearson. 135-155.
- Serway, R., Vulle, C. 2011. Fundamentals of Physics. 9na Cengage læring. 172-182
- Tipler, P. (2006) Fysik til videnskab og teknologi. 5. udg. Bind 1. Editorial Reverté. 217-238
- Tippens, P. 2011. Fysik: begreber og applikationer. 7. udgave. MacGraw Hill. 185-195



Endnu ingen kommentarer