
Væsentlige figurer regler, eksempler, løste øvelser
Er navngivet Væsentlige tal til antallet af cifre indeholdt i mantissa af et nummer. Jo flere tal du har, jo mere præcist er mængden kendt. Som en påmindelse er mantissen den figur, der ledsager kraften på 10, når tallet er skrevet i videnskabelig notation..
Lad os for eksempel tage tallet 0,00376, som er skrevet som 3,76 x 10 -3. Mantissen er 3,76, og antallet har i alt 3 signifikante tal. Tallet 0,129 har også 3 signifikante tal, mens 4,5 kun har 2.

Og hvad sker der, når tallet er et heltal? Det betyder, at det er kendt med så meget præcision som muligt, med andre ord, det har uendelig præcision. Når man f.eks. Tæller mennesker, dyr eller genstande som bøger og telefoner, er resultatet et præcist heltal.
Hvis vi siger, at der i en biograf er 110 mennesker, der ser en film, er dette det nøjagtige antal, hverken mere eller mindre, og det har 3 betydende tal.
Væsentlige tal håndteres af nogle enkle regler, der huskes med lidt øvelse, som vi vil se nedenfor..
Artikelindeks
- 1 Regler til bestemmelse af de væsentlige tal for et tal
- 1.1 Regel 1
- 1.2 Regel 3
- 1.3 Regel 4
- 1.4 Regel 5
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 2.3 Eksempel 3
- 3 Regler for afrunding af numre
- 4 Referencer
Regler til bestemmelse af de væsentlige tal for et tal
Regel 1
De forreste nuller tæller ikke som et signifikant tal, så 0,045 og 4,5 har begge to signifikante tal, da disse begynder at tælles fra venstre og starter fra det første ikke-nul ciffer.
Regel 2
Nullerne efter (til højre) det første signifikante ciffer tæller som en væsentlig figur (så længe det er berettiget af måleinstrumentets præcision).
Endelig tælles nuller i midten også som et signifikant ciffer..
Regel 3
For tal skrevet i videnskabelig notation er alle figurer i mantissa signifikante, og eksponenten påvirker ikke præcisionen..
Regel 4
Når du udfører operationer med decimaler, f.eks. Ved beregning af arealer eller andre lignende operationer, skal resultatet have det samme antal signifikante tal som mængden med det færreste antal signifikante tal, der deltog i operationen. Denne regel er gyldig for enhver aritmetisk operation.
Regel 5
Tegnet på nummeret påvirker ikke antallet af væsentlige tal.
Vi vil straks se nogle eksempler på dette og alle de andre regler.
Eksempler
Eksempel 1
Find ud af, hvor mange vigtige tal der er i hvert af disse tal.
a) 876
b) 1000,68
c) 0,00005026
d) 4.8
e) -6,99
Svar
a) 876 har 3 signifikante tal.
b) 1000.68 har 6 signifikante tal, da nuller imellem tæller som sådan.
c) I stedet har 0.00005026 4 signifikante tal. Bemærk, at de 5 nuller til venstre for 5 ikke tælles som et væsentligt tal, i stedet for 0, der er mellem 5 og 2..
d) 4.8 har 2 signifikante tal.
e) -6.99 har 3 signifikante tal.
Eksempel 2
Det er almindeligt at tage målinger med måleinstrumenter, såsom målebånd, ure, termometre, skalaer og så videre. Med hvor mange væsentlige tal skal vi rapportere de mængder, vi måler på denne måde??
Svar
Det afhænger af påskønnelsen af det instrument, som det måles med. Lad os tage et eksempel: måle den ydre diameter af et rør med en gradueret lineal og med en vernier eller tykkelse.
Vernier er et instrument, der måler længder meget præcist, fordi det har en ekstra lille skala, kaldet vernier, hvilket muliggør større finhed, så at sige, når man måler.
Det er mere præcist end en gradueret linjal, for med den kan vi kende mere betydningsfulde figurer af en bestemt længde.
Derfor giver det ingen mening at rapportere en omkreds på f.eks. 35,88 cm, hvis vi måler det med et målebånd, da dette instrument ikke er nøjagtigt nok til at rapportere så mange signifikante cifre..
Påskønnelsen A af målebåndet gives af:
Eksempel 3
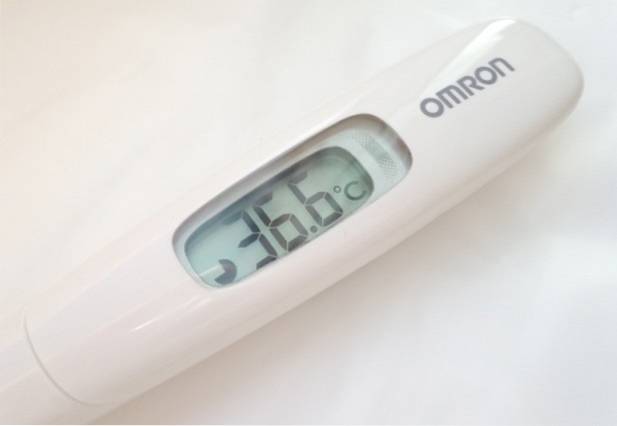
Hvor mange vigtige tal har læsningen foretaget med det digitale termometer?
Svar
Termometeret i figuren giver tre-cifrede temperaturaflæsninger. I den viste måling, 36,6 ºC, er det dog kun de første to cifre fra venstre mod højre, der er nøjagtige, da decimaltallet påvirkes af instrumentets påvisningsfejl, som normalt er angivet på bagsiden af instrumentet eller din betjeningsvejledning.
Det sædvanlige for den viste type digitale instrument er en fejltagelse på 0,1 ºC. Dette er nok til at være sikker på, at du ikke har feber..

Regler for afrunding af tal
Når du bruger en lommeregner til at udføre beregninger med opnåede målinger, er det ikke korrekt at give resultatet ved hjælp af alle de cifre, der vises på skærmen.
Kun de, der er nøjagtigt kendte, bevares, da kun de har ægte betydning. Det er derefter nødvendigt at afrunde resultaterne, så de passer til antallet af nøjagtigt kendte tal. Disse regler er:
-Hvis nummeret efter cifret, der skal tilbageholdes, er lig med eller større end 5, 1 føjes til dette ciffer.
For eksempel, når vi afrunder 3.786 til to decimaler, vil vi bevare tallene op til 8. Da antallet, der følger (6) er større end 5, bliver 8 til 8 + 1 = 9, og tallet forbliver som 3,79.
-Når tallet efter cifret, der skal holdes, er mindre end 5, cifferet forbliver det samme.
Hvis vi vil afrunde 1.27924, så den kun har 3 decimaler, opnås dette ved at nå 9, som efterfølges af 2. Da 2 er mindre end 5, forsvinder disse decimaler, og det afrundede tal forbliver 1,279.
Træning løst
Et spisebord har den form og dimensioner, der er angivet i den ledsagende figur. Du bliver bedt om at beregne dets område ved hjælp af driftsreglerne med betydelige tal.
Opløsning
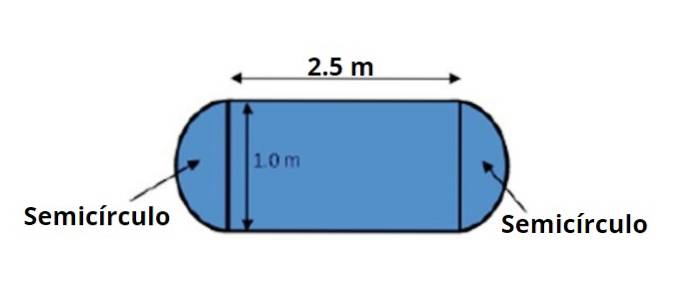
Bordområdet kan opdeles i et centralt rektangulært område og to halvcirkler, en på hver side, som tilsammen udgør 1 fuld cirkel.
Vi kalder A1 til rektangelområdet, givet af:
TIL1 = bund × højde = 2,5 m x 1,0 m = 2,5 mto
For sin del er arealet af cirklen, der er lig med det for en halvcirkel ganget med 2:
TILto = π × radiusto
Diameteren på en hvilken som helst af halvcirklerne er 1,0 m, derfor er radiusen 0,50 m. Diameteren kunne også bruges direkte til at beregne arealet, i dette tilfælde:
TILto = (π × diameterto) / 4
Under alle omstændigheder:
TILto = [π x (1,0 m)to] / 4 = 0,785398163 mto
Alle cifre leveret af lommeregneren blev brugt. Nu tilføjer vi A1 alleredeto for det samlede areal A i tabellen:
A = (2,5 + 0,785398163) mto = 3.285398163 mto
Da dimensionerne på tabellen er kendt for to signifikante tal, giver det ikke mening at udtrykke resultatet med alle decimaler, der er angivet af regnemaskinen, hvilket aldrig giver antallet af signifikante tal for et resultat.
Hvad du skal gøre er at afrunde området, så det har samme antal signifikante figurer som dimensionerne på tabellen, dvs. 2. Det endelige resultat rapporteres derfor som følger:
A = 3,3 mto
Referencer
- Bauer, W. 2011. Fysik til ingeniørvidenskab. Bind 1. Mc Graw Hill.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 1. kinematik. Redigeret af Douglas Figueroa (USB).
- Fisicalab. Væsentlige tal og afrunding. Gendannet fra: fisicalab.com.
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.



Endnu ingen kommentarer