Det restitutionskoefficient er kvotienten mellem den relative tilbagetrækningshastighed og den relative tilgangshastighed for to kolliderende legemer. Når ligene er samlet efter kollisionen, er denne kvotient nul. Og enheden er værd, hvis kollisionen er perfekt elastisk.
Antag to faste massesfærer M1 og masse M2 henholdsvis der lider af en kollision. Lige før kollisionen havde kuglerne hastigheder V1 Y V2 med hensyn til et bestemt inertialreferencesystem. Lige efter kollisionen skifter deres hastighed til V1 ' Y V2 '.
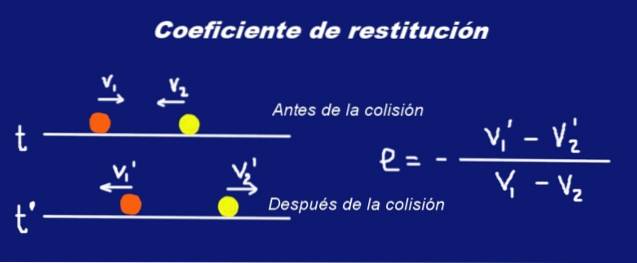
Brevet er placeret fed skrift i hastighederne for at indikere, at de er vektorstørrelser.
Eksperimenter indikerer, at hver kollision opfylder følgende forhold:
V1 ' - V2 '= -og (V1 - V2)
Hvor og er et reelt tal mellem 0 og 1, kaldet restitutionskoefficient af kollisionen. Ovenstående udtryk fortolkes således:
Den relative hastighed af to partikler før kollisionen er proportional med den relative hastighed af de to partikler efter kollisionen, proportionalitetskonstanten er (-e), hvor e er koefficienten for restitution af kollisionen.
Artikelindeks
Nytten af denne koefficient ligger i at kende grad af uelasticitet af en kollision. I tilfælde af at kollisionen er perfekt elastisk, vil koefficienten være 1, mens koefficienten i en fuldstændig uelastisk kollision er 0, da den relative hastighed efter kollisionen i dette tilfælde er nul..
Omvendt, hvis koefficienten for genopretning af en kollision og hastighederne på partiklerne før den er kendt, kan hastighederne efter kollisionen forudsiges..
Foruden sammenhængen, der fastlægger restitutionskoefficienten, er der i kollisioner et andet grundlæggende forhold, som er bevarelse af momentum.
Momentum s af en partikel eller momentum, som det også kaldes, er massens produkt M af partiklen ved dens hastighed V. Det vil sige: momentum s er en vektormængde.
I kollisioner er det lineære momentum P af systemet er det samme lige før og lige efter kollisionen, fordi de eksterne kræfter er ubetydelige sammenlignet med de korte, men intense kræfter af intern interaktion under kollisionen. Men bevarelse af momentum er ikke nok P af systemet for at løse det generelle problem med kollision.
I det tidligere nævnte tilfælde, at for de to kolliderende sfærer af masserne M1 og M2, er bevarelsen af det lineære momentum skrevet som følger:
M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .
Der er ingen måde at løse kollisionsproblemet på, hvis restitutionskoefficienten ikke er kendt. Bevarelse af momentum er, selvom det er nødvendigt, utilstrækkelig til at forudsige hastigheder efter kollision.
Når et problem siger, at ligene forbliver i bevægelse efter kollisionen, siger det implicit, at restitutionskoefficienten er 0.
Den anden vigtige fysiske størrelse involveret i kollisioner er energi. Under kollisioner er der udveksling af kinetisk energi, potentiel energi og andre typer energi, såsom varmeenergi.
Før og efter sammenstødet er interaktionens potentielle energi praktisk talt nul, så energibalancen involverer partiklernes kinetiske energi før og efter og en mængde Spørgsmål kaldet spredt energi.
For de to kolliderende massesfærer M1 og M2 skrives energibalancen før og efter kollisionen som følger:
½ M1 V1^ 2 + ½ M2 V2^ 2 = ½ M1 V1 '^ 2 + ½ M2 V2 '^ 2 + Q
Når interaktionskræfterne under kollisionen er rent konservative, sker det, at total kinetisk energi af de kolliderende partikler er konserveret, dvs. det er det samme før og efter kollisionen (Q = 0). Når dette sker, siges kollisionen at være perfekt elastisk..
I tilfælde af elastiske kollisioner spredes ingen energi. Og desuden er restitutionskoefficienten i overensstemmelse med: e = 1.
Tværtimod i de uelastiske kollisioner Q ≠ 0 og 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.
For at et kollisionsproblem kan bestemmes perfekt, er det nødvendigt at kende restitutionskoefficienten eller alternativt mængden af energi, der spredes under kollisionen.
Restitutionskoefficienten afhænger af arten og typen af interaktion mellem de to kroppe under kollisionen..
På sin side vil kroppens relative hastighed før kollisionen definere intensiteten af interaktionen og dermed dens indflydelse på restitutionskoefficienten..
For at illustrere hvordan beregningskoefficienten for en kollision beregnes, tager vi et simpelt tilfælde:
Antag sammenstød mellem to massesfærer M1 = 1 kg Y M2 = 2 kg bevæger sig på en lige skinne uden friktion (som i figur 1).
Den første kugle rammer med starthastighed V1 = 1 m / s på det andet, der oprindeligt er i ro, altså V2 = 0 m / s.
Efter sammenstødet bevæger de sig sådan: den første stopper (V1 '= 0 m / s) og det andet bevæger sig til højre med hastighed V2 '= 1/2 m / s.
For at beregne restitutionskoefficienten i denne kollision anvender vi forholdet:
V1 ' - V2 ' = -og ( V1 - V2 )
0 m / s - 1/2 m / s = - e (1 m / s - 0 m / s) => - 1/2 = - e => e = 1/2 .
I den endimensionelle kollision mellem de to kugler i det foregående afsnit blev deres restitutionskoefficient beregnet, hvilket resulterede i e = ½ .
Da e ≠ 1 er kollisionen ikke elastisk, dvs. systemets kinetiske energi bevares ikke, og der er en vis mængde spredt energi Q (for eksempel opvarmning af kuglerne på grund af kollisionen).
Bestem værdien af den energi, der spredes i Joule. Beregn også den procentvise brøkdel af energi, der er spredt.
Den oprindelige kinetiske energi i sfære 1 er:
K1i = ½ M1 V1 ^ 2 = ½ 1 kg (1 m / s) ^ 2 = ½ J
mens sfære 2 er nul, fordi den oprindeligt er i ro.
Derefter er systemets indledende kinetiske energi Ki = ½ J.
Efter kollisionen bevæger sig kun den anden kugle med hastigheden V2 '= ½ m / s, så systemets endelige kinetiske energi vil være:
Kf = ½ M2 V2 '^ 2 = ½ 2 kg (½ m / s) ^ 2 = ¼ J
Det vil sige, at energien spredt i kollisionen er:
Q = Ki - Kf = (½ J - ¼ J) = 1/4 J
Og den brøkdel af energi, der spredes ved denne kollision, beregnes som følger:
f = Q / Ki = ¼ / ½ = 0,5, det vil sige at 50% af systemets energi er spredt på grund af den uelastiske kollision, hvis restitutionskoefficient er 0,5.
Endnu ingen kommentarer