Det komprimerbarhed af et stof eller materiale er den ændring i volumen, som den oplever, når den udsættes for en trykændring. Generelt falder lydstyrken, når der påføres tryk på et system eller en genstand. Imidlertid sker der undertiden det modsatte: en trykændring kan frembringe en eksplosion, hvor systemet øges i volumen, eller når en faseændring finder sted..
I nogle kemiske reaktioner kan dette ske og også i gasser, da de afstødende kræfter finder sted, når frekvensen af kollisioner øges..
Når du forestiller dig, hvor let eller vanskeligt det kan være at komprimere et objekt, skal du overveje de tre tilstande, der betyder noget normalt, er: fast, flydende og gas. I hver af dem holder molekylerne visse afstande fra hinanden. Jo stærkere bindinger, der forbinder molekylerne i stoffet, der udgør objektet, og jo tættere de er, desto vanskeligere vil det være at forårsage en deformation.
Et fast stof har sine molekyler meget tæt på hinanden, og når man prøver at bringe dem tættere på hinanden, vises frastødende kræfter, der gør opgaven vanskelig. Derfor siges det, at faste stoffer ikke er særlig komprimerbare. I væskemolekylerne er der mere plads, så deres kompressibilitet er større, men alligevel kræver volumenændringen normalt store kræfter.
Så faste stoffer og væsker er næppe komprimerbare. Det ville kræve en meget stor trykvariation for at opnå en mærkbar volumenændring under såkaldte normale tryk- og temperaturforhold. På den anden side komprimeres og dekomprimeres let gasser, da deres molekyler er bredt adskilt.
Artikelindeks
Når en genstand for eksempel nedsænkes i en væske, udøver den pres på genstanden i alle retninger. På denne måde kan vi tro, at genstandens volumen vil falde, selvom dette i de fleste tilfælde ikke vil være mærkbart..
Situationen kan ses i følgende figur:
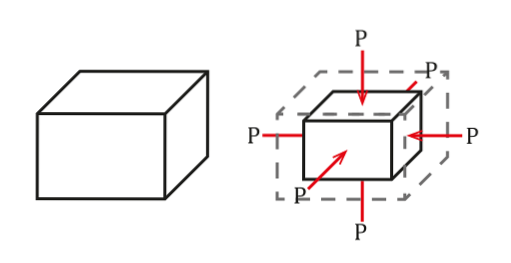
Tryk defineres som kraft pr. Arealeenhed, hvilket vil medføre en volumenændring AV proportional med det oprindelige volumen af objektet Veller. Denne volumenændring afhænger af dens kvaliteter..
Hookes lov siger, at deformationen, som en genstand oplever, er proportional med den belastning, der påføres den:
Stress ∝ Stamme
Den volumetriske deformation, der opleves af et legeme, kvantificeres ved B den krævede proportionalitetskonstant, der kaldes materialets volumetriske modul:
B = -Stress / Stamme
B = -ΔP / (AV / Veller)
Som AV / Veller er en dimensionsløs størrelse, da det er kvotienten mellem to volumener, har det volumetriske modul de samme trykenheder, som i det internationale system er Pascal (Pa).
Det negative tegn angiver den forventede reduktion i volumen, når objektet er komprimeret nok, det vil sige, at trykket stiger.
Den omvendte eller gensidige værdi af det volumetriske modul kaldes komprimerbarhed og er betegnet med brevet k. Derfor:
Her k er negativt af den fraktionerede volumenændring pr. trykstigning. Dens enheder i det internationale system er inverserne af Pa, det vil sige mto / N.
Ligningen for B eller for k, hvis du foretrækker det, gælder for både faste stoffer og væsker. Begrebet volumetrisk modul anvendes sjældent på gasser. En simpel model til at kvantificere volumenfaldet, som en ægte gas kan opleve, forklares nedenfor..
En interessant applikation er lydens hastighed i et medium, hvilket afhænger af dets kompressibilitetsmodul:
En massiv messingkugle, hvis volumen er 0,8 m3 det falder ned i havet til en dybde, hvor det hydrostatiske tryk er 20 M Pa større end ved overfladen. Hvordan vil kuglens volumen ændre sig? Det er kendt, at messingens kompressibilitetsmodul er B = 35.000 MPa,
1 M Pa = 1 Mega pascal = 1. 10 6 Pa
Trykvariationen i forhold til overfladen er DP = 20 x 10 6 Pa. Anvendelse af ligningen for B har vi:
B = -ΔP / (AV / Veller)
Derfor:
AV = -5,71.10 -4 x 0,8 m3 = -4,57 x 10-4 m3
Volumenforskellen kan have et negativt tegn, når den endelige lydstyrke er mindre end den oprindelige lydstyrke, derfor stemmer dette resultat overens med alle de antagelser, vi hidtil har gjort.
Den meget høje kompressibilitetsmodul indikerer, at der kræves en stor ændring i tryk for at genstanden skal opleve et mærkbart fald i volumen..
Ved at sætte øret mod jernbanesporene kan du se, hvornår et af disse køretøjer nærmer sig i det fjerne. Hvor lang tid tager lyden, når man kører på en stålskinne, hvis toget er 1 km væk?
Ståldensitet = 7,8 x 10 3 kg / m3
Stålkompressibilitetsmodul = 2,0 x 10 elleve Pa.
Ovenstående beregningsmodul B beregnes også for væsker, skønt der generelt kræves en stor indsats for at frembringe et mærkbart fald i volumen. Men væsker kan ekspandere eller trække sig sammen, når de opvarmes eller køler ned, og ligeledes hvis de er under tryk eller under tryk..
For vand under standardbetingelser for tryk og temperatur (0 ° C og en atmosfæretryk ca. eller 100 kPa) er det volumetriske modul 2100 MPa. Det vil sige ca. 21.000 gange atmosfæretrykket.
Af de grund betragtes væsker i de fleste anvendelser normalt som ukomprimerbare. Dette kan kontrolleres med det samme med numerisk anvendelse.
Find det fraktionerede fald i vandvolumen, når det udsættes for et tryk på 15 MPa.
Som beskrevet ovenfor fungerer gasser lidt anderledes.
At vide, hvilket volumen de har n mol af en given gas, når den holdes begrænset ved et tryk P og ved en temperatur T, tilstandsligningen bruges. I tilstandsligningen for en ideel gas, hvor intermolekylære kræfter ikke tages i betragtning, siger den enkleste model at:
P.Videel = n. R. T
Hvor R er den ideelle gaskonstant.
Ændringer i gasvolumen kan udføres ved konstant tryk eller konstant temperatur. For eksempel ved at holde temperaturen konstant, er den isotermiske kompressibilitet ΚT det er:
I stedet for symbolet "delta", der blev brugt før ved definition af konceptet for faste stoffer, beskrives det for en gas med et derivat, i dette tilfælde delvis derivat med hensyn til P og holder T konstant.
Derfor BT den isotermiske kompressibilitetsmodul er:
Og den adiabatiske kompressibilitetsmodul B er også vigtig.adiabatisk, som der ikke er nogen indgående eller udgående varmestrøm for.
Badiabatisk = γp
Hvor γ er den adiabatiske koefficient. Med denne koefficient kan lydhastigheden i luft beregnes:
Anvend ovenstående ligning, find lydens hastighed i luften.
Luftens adiabatiske kompressibilitetsmodul er 1,42 × 105 Pa
Densiteten af luft er 1.225 kg / m3 (ved atmosfærisk tryk og 15 ºC)
I stedet for at arbejde med kompressibilitetsmodulet, som en enhedsændring i volumen pr. Trykændring, kompressibilitetsfaktor for en reel gas, et andet, men illustrerende koncept for, hvordan ægte gas sammenlignes med idealgas:
P. Vægte = Z. R. T
Hvor Z er kompressibilitetskoefficienten for gassen, som afhænger af de betingelser, hvori den findes, generelt er en funktion af både trykket P og temperaturen T og kan udtrykkes som:
Z = f (P, T)
I tilfælde af en idealgas Z = 1. For ægte gasser stiger Z-værdien næsten altid med tryk og falder med temperaturen.
Når trykket stiger, kolliderer de gasformige molekyler oftere, og de frastødende kræfter mellem dem øges. Dette kan føre til en stigning i volumen i den virkelige gas, hvorved Z> 1.
I modsætning hertil er molekylerne ved lavere tryk frie til at bevæge sig, og tiltrækningskræfter dominerer. I et sådant tilfælde Z < 1.
For det enkle tilfælde af 1 mol gas n = 1, hvis de samme tryk- og temperaturforhold opretholdes, ved at dividere de foregående ligninger på term, får vi:
Vægte = Z Videel
Der er en reel gas ved 250 ºK og et tryk på 15 atm, som har et molært volumen, der er 12% mindre end det, der beregnes ved den ideelle gasligning af tilstanden. Hvis tryk og temperatur holdes konstant, skal du finde:
a) Kompressionsfaktoren.
b) Den molære mængde af den virkelige gas.
c) Hvilken type kræfter dominerer: tiltrækkende eller frastødende?
a) Hvis det virkelige volumen er 12% mindre end idealet, betyder det at:
Vægte = 0,88 Videel
Derfor er kompressibilitetsfaktoren for 1 mol gas:
Z = 0,88
b) Valg af den ideelle gaskonstant med de passende enheder til de leverede data:
R = 0,082 L.atm / mol.K
Det molære volumen beregnes ved at løse og erstatte værdier:
c) Attraktionskræfter dominerer, da Z er mindre end 1.
Endnu ingen kommentarer