
Ligevægtskoncept, applikationer og eksempler
Det ligevægtsbetingelser De er nødvendige for, at en krop forbliver i ro eller i ensartet retlinet bevægelse. I det første tilfælde siges det, at objektet er i statisk ligevægt, mens det andet er i dynamisk ligevægt.
Under forudsætning af at den bevægelige genstand er en partikel, i hvilket tilfælde dimensionerne ikke tages i betragtning, er det nok, at summen af kræfter, der virker på den, annulleres.

Men et stort flertal af bevægelige objekter har mærkbare dimensioner, derfor er denne tilstand ikke nok til at garantere ligevægt, hvilket under alle omstændigheder er fraværet af acceleration, ikke bevægelse..
Artikelindeks
- 1 Første og anden ligevægtstilstand
- 2 applikationer
- 2.1 Isostatisk ligevægt
- 2.2 Hvordan fusion fungerer i kernen
- 2.3 Konstruktion
- 3 Typer af statisk ligevægt
- 3.1 Stabil ligevægt
- 3.2 Ligegyldig eller neutral balance
- 3.3 Ustabil ligevægt
- 4 Eksempel: partikelstatik
- 5 Øvelse løst
- 5.1 Løsning
- 6 Emner af interesse
- 7 Referencer
Første og anden ligevægtstilstand
Lad os se: hvis summen af kræfter er nul, er det rigtigt, at objektet ikke bevæger sig eller bevæger sig med en accelereret hastighed, men det kan stadig begynde at rotere.
Derfor, for at undgå rotationer, skal der tilføjes en anden betingelse: at summen af drejningsmomenterne eller vridningsmomenterne forårsaget af eksterne kræfter, der virker på det, omkring ethvert punkt, også annulleres..
Kort sagt betegner som F nettokraftvektoren y τ eller M til nettomomentvektoren har vi:
Første ligevægtstilstand
∑ F = 0
Hvilket betyder, at: ∑ Fx = 0, ∑ FY = 0 og ∑ Fz = 0
Anden ligevægtstilstand
∑ τ = 0 eller ∑ M = 0
Med drejningsmomenterne eller momentene beregnet til ethvert punkt.
I det følgende antager vi, at den bevægelige genstand er en stiv krop, en der ikke gennemgår nogen deformation..
Ansøgninger
På trods af at bevægelse synes at være den fællesnævner i universet, er balance også til stede i mange aspekter af naturen og i objekterne, der omgiver os..
Isostatisk ligevægt
På planetarisk skala er Jorden inde isostatisk ligevægt, en slags tyngdevægt af jordskorpen, hvis densitet ikke er ensartet.
Forskellene i tæthederne for de forskellige blokke eller områder af jordskorpen kompenseres af forskellene i højden, der kendetegner planetens orografi. Det fungerer på samme måde, at forskellige materialer er mere eller mindre nedsænket i vand i henhold til deres tæthed og når ligevægt.
Men da skorpeblokkene ikke flyder ordentligt i vand, men i kappen, som er meget mere tyktflydende, kaldes ligevægten ikke hydrostatisk, men isostatisk..
Hvordan fusion fungerer i kernen
I stjerner som vores sol holder balancen mellem tyngdekraften, der komprimerer dem, og det hydrostatiske tryk, der udvider dem, fusionsreaktoren i kernen af stjernen i gang, hvilket holder den i live. Vi er afhængige af denne balance for at Jorden kan modtage det nødvendige lys og varme.
Bygning
I lokal skala ønsker vi, at bygninger og konstruktioner skal forblive stabile, dvs. overholde ligevægtsbetingelser, især statisk ligevægt..
Derfor opstod der statik, som er en gren af mekanik, der er dedikeret til at studere balancen mellem kroppe og alt, hvad der er nødvendigt for at holde dem på den måde..
Typer af statisk ligevægt
I praksis finder vi, at statisk ligevægt kan være af tre slags:
Stabil ligevægt
Det sker, når objektet bevæger sig fra sin position og straks vender tilbage til det, når kraften, der skubbede det væk, ophører. Jo tættere et objekt er på jorden, jo mere sandsynligt er det at være i stabil ligevægt.
Kuglen til højre i figur 2 er et godt eksempel, hvis vi fjerner den fra sin ligevægtsposition i bunden af skålen, vil tyngdekraften sørge for dens hurtige tilbagevenden.
Ligegyldig eller neutral balance
Det sker, når objektet, selvom det er flyttet, stadig er i balance. Runde genstande som kuglen, når de placeres på flade overflader, er i ligegyldig ligevægt.
Ustabil balance
Det sker, når objektet bevæger sig fra sin ligevægtsposition, vender det ikke tilbage til det. Hvis vi flytter bolden væk fra toppen af bakken til venstre, er det sikkert, at den ikke vender tilbage under egen kraft..

Eksempel: partikelstatik
Antag en blok af masse m på et skråt plan, hvor al masse antages at være koncentreret i dets geometriske centrum.
Den vandrette komponent af vægten Wx det har tendens til at få blokken til at glide ned ad bakke, derfor er der brug for en anden modsatrettede kraft. Hvis vi vil have blokken i ro, er denne kraft den statiske friktion. Men hvis vi tillader blokken at glide ned ad bakke med konstant hastighed, er den krævede kraft dynamisk friktion..
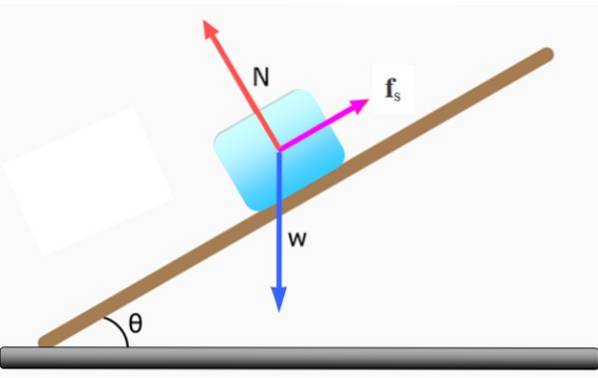
I mangel af friktion glider blokken hurtigt ned ad bakke, og i dette tilfælde vil der ikke være nogen ligevægt.
For at blokken skal hvile, er de kræfter, der virker på den: vægt W, det normale N og den statiske friktion Fs, de skal kompenseres. Derefter:
∑ FY = 0 → N - WY = 0
∑ Fx = 0 → Wx - Fs = 0
Statisk friktion afbalancerer den vandrette komponent af vægten: Wx = fs og derfor:
Fs = m. g .sen θ
Træning løst
Et 21,5 kg trafiklys hænger fra en homogen aluminiumsstang AB med en vægt på 12 kg og 7,5 m, understøttet af en vandret reb-CD, som vist i figuren. Finde:
a) DC-kabels spænding
b) De vandrette og lodrette komponenter af den kraft, der udøves af sving A på stolpen.
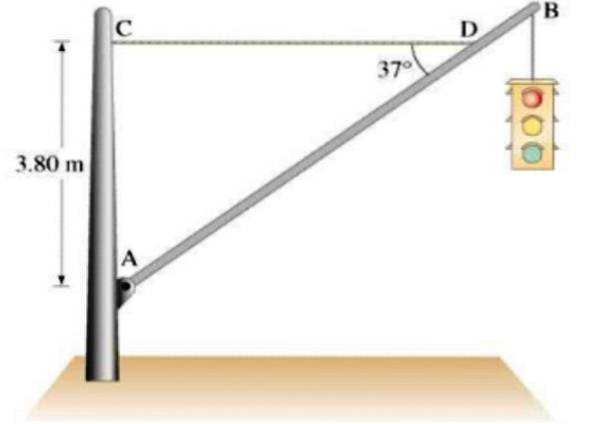
Opløsning
Diagrammet over kræfter, der påføres stangen, er konstrueret med vægten W, spændingerne i akkorderne og de vandrette og lodrette komponenter i drejereaktionen, kaldet Rx og RY. Derefter gælder ligevægtsbetingelser.
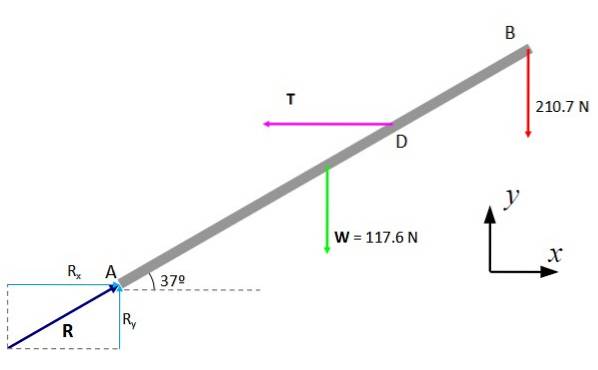
Første betingelse
At være et problem i planet, den første ligevægtstilstand tilbyder to ligninger:
ΣFx = 0
ΣFY = 0
Fra den første:
Rx - T = 0
Rx = T
Og det andet:
RY - 117,6 N - 210,7 N = 0
RY = 328,3 N
Den vandrette komponent i reaktionen er lig med størrelsen på spændingen T.
Anden betingelse
Punkt A i figur 5 vælges som omdrejningspunkt, på denne måde reaktionsarmen R er nul, husk at øjeblikkets størrelse er givet af:
M = F┴ d
Hvor F┴ er kraftens vinkelrette komponent, og d er afstanden mellem rotationsaksen og kraftens påføringspunkt. Vi får en ligning:
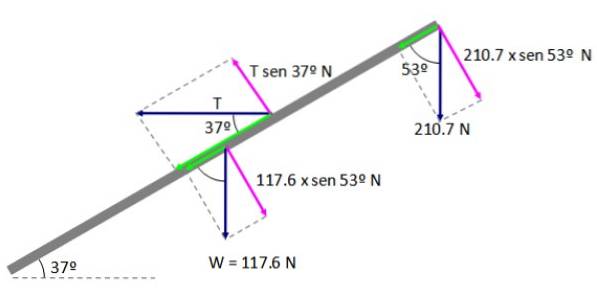
ΣMTIL = 0
(210,7 × sin 53º) AB + (117,6 × sin 53º) (AB / 2) - (T × sin 37º) AD = 0
Afstanden AD er:
AD = (3,8 m / sin 37º) = 6,3 m
(210,7 × sin 53º N) (7,5 m) + (117,6 × sin 53º N) (3,75 m) - (T × sin 37º N) (6,3 m) = 0
Udførelse af de angivne operationer:
1262.04 + 352.20 - 3.8T = 0
Løsning for T opnår vi:
T = 424,8 N
Fra den første betingelse, Rx = T, derfor:
Rx = 424,8 N
Temaer af interesse
Første ligevægtstilstand.
Anden ligevægtstilstand.
Referencer
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fysik til videnskab og teknik. Bind 4. Partikelsystemer. Redigeret af Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysik: Principper med applikationer. 6. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysik med moderne fysik. 14. Red. Bind 1.
- Wikipedia. Isostasia. Gendannet fra: es.wikipedia.org.



Endnu ingen kommentarer