
Konstant af integration betydning, beregning og eksempler

Det konstant integration Det er en merværdi til beregningen af antiderivativer eller integraler, den tjener til at repræsentere de løsninger, der udgør en funktions primitive. Udtryk en iboende tvetydighed, hvor enhver funktion har et uendeligt antal primitiver.
Hvis vi f.eks. Tager funktionen: f (x) = 2x + 1, og vi får dens antiderivative:
∫ (2x + 1) dx = xto + x + C ; Hvor C er konstant integration og repræsenterer grafisk den lodrette oversættelse mellem primitivens uendelige muligheder. Det er korrekt at sige det (xto + x) er -en af primitiverne for f (x).
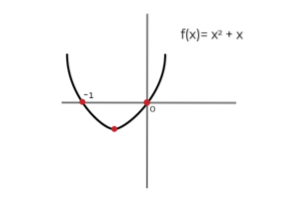
På samme måde kan vi definere en (xto + x + C ) som primitiv for f (x).
Artikelindeks
- 1 Omvendt egenskab
- 2 Den ubestemte integral
- 3 Andre betydninger af konstant integration
- 4 Hvordan beregnes integrationskonstanten?
- 5 eksempler
- 5.1 Eksempel 1
- 5.2 Eksempel 2
- 5.3 Eksempel 3
- 6 Foreslåede øvelser
- 6.1 Øvelse 1
- 6.2 Øvelse 2
- 6.3 Øvelse 3
- 6.4 Øvelse 4
- 7 Referencer
Omvendt ejendom
Det kan bemærkes, at ved at aflede udtrykket (xto + x) funktionen f (x) = 2x + 1 opnås. Dette skyldes den omvendte egenskab, der findes mellem afledningen og integrationen af funktioner. Denne egenskab gør det muligt at opnå integrationsformler startende fra differentieringen. Hvilket tillader verifikation af integraler gennem de samme derivater.
Dog (xto + x) er ikke den eneste funktion, hvis afledte er lig med (2x + 1).
- d (xto + x) / dx = 2x + 1
- d (xto + x + 1) / dx = 2x + 1
- d (xto + x + 2) / dx = 2x + 1
- d (xto + x + 3) / dx = 2x + 1
- d (xto + x + C) / dx = 2x + 1
Hvor 1, 2, 3 og 4 repræsenterer bestemte primitiver af f (x) = 2x + 1. Mens 5 repræsenterer den ubestemte eller primitive integral af f (x) = 2x + 1.
Primitiverne for en funktion opnås gennem antiderivation eller integreret proces. Hvor F vil være en primitiv af f, hvis følgende er sandt
- y = ∫ f (x) dx = F (x) + C; C = konstant integration
- F '(x) = f (x)
Det kan ses, at en funktion har et enkelt derivat, i modsætning til dets uendelige primitiver som følge af integration.
Den ubestemte integral
∫ f (x) dx = F (x) + C.
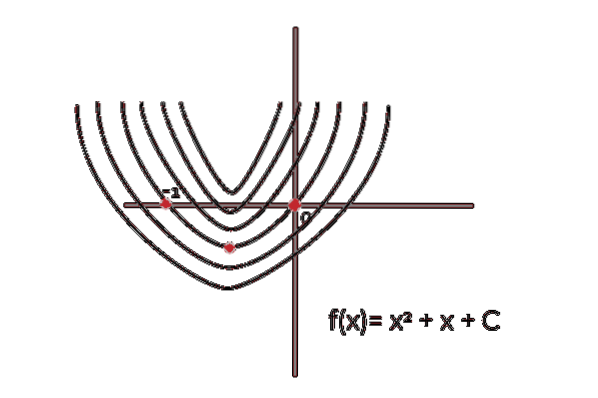
Det svarer til en familie af kurver med det samme mønster, der oplever uoverensstemmelse i værdien af billederne for hvert punkt (x, y). Hver funktion, der opfylder dette mønster, vil være en individuel primitiv, og sættet med alle funktioner er kendt som ubestemt integral.
Værdien af konstant integration vil være den, der adskiller hver funktion i praksis.
Det konstant integration foreslår et lodret skift i alle grafer, der repræsenterer primitiverne for en funktion. Hvor paralleliteten mellem dem observeres, og det faktum at C er værdien af forskydningen.
I henhold til almindelig praksis konstant integration det er betegnet med bogstavet "C" efter et addend, skønt det i praksis ikke betyder noget, om konstanten tilføjes eller trækkes fra. Dens reelle værdi kan findes på forskellige måder efter forskellige indledende betingelser.
Andre betydninger af konstant integration
Det blev allerede talt om, hvordan konstant integration anvendes i grenen af integreret beregning; Repræsenterer en familie af kurver, der definerer den ubestemte integral. Men mange andre videnskaber og grene har tildelt meget interessante og praktiske værdier konstant integration, der har lettet udviklingen af flere studier.
I fysisk konstanten af integration kan tage flere værdier afhængigt af dataens art. Et meget almindeligt eksempel er at kende funktionen V (t) som repræsenterer hastighed af en partikel versus tid t. Det er kendt, at når man beregner en primitiv af V (t), opnås funktionen R (t) som repræsenterer position partikel versus tid.
Det konstant integration repræsenterer værdien af startpositionen, dvs. på tidspunktet t = 0.
Tilsvarende, hvis funktionen er kendt A (t) som repræsenterer acceleration af partiklen versus tid. Den primitive af A (t) vil resultere i funktionen V (t), hvor konstant integration vil være værdien af starthastigheden V.0.
I økonomi, ved at opnå ved hjælp af integration det primitive af en omkostningsfunktion. Det konstant integration repræsenterer faste omkostninger. Og så mange andre applikationer, der fortjener differentieret og integreret beregning.
Hvordan beregnes integrationskonstanten?
For at beregne konstant integration, det vil altid være nødvendigt at kende indledende betingelser. Hvilke er ansvarlige for at definere, hvilke af de mulige primitiver, der er de tilsvarende.
I mange applikationer behandles det som en uafhængig variabel på tidspunktet (t), hvor konstanten C tager de værdier, der definerer indledende betingelser i den særlige sag.
Hvis vi tager det indledende eksempel: ∫ (2x + 1) dx = xto + x + C
En gyldig startbetingelse kan være at betingelsen om, at grafen passerer gennem en bestemt koordinat. For eksempel er det kendt, at den primitive (xto + x + C) passerer gennem punktet (1, 2)
F (x) = xto + x + C; dette er den generelle løsning
F (1) = 2
Vi erstatter den generelle løsning i denne lighed
F (1) = (1)to + (1) + C = 2
Fra hvor det let følger det C = 0
På denne måde er den tilsvarende primitive for denne sag F (x) = xto + x
Der er flere typer numeriske øvelser, der arbejder med konstanter af integration. Faktisk holder differentierings- og integralregningen ikke op med at blive anvendt i aktuelle undersøgelser. På forskellige akademiske niveauer kan de findes; fra den indledende beregning gennem fysik, kemi, biologi, økonomi, blandt andre.
Det ses også i undersøgelsen af differentialligninger, hvor er konstant integration Det kan tage forskellige værdier og løsninger, dette på grund af de mange afledninger og integrationer, der udføres i denne sag.
Eksempler
Eksempel 1
- En 30 meter høj kanon affyrer et projektil lodret opad. Projektilets indledende hastighed vides at være 25 m / s. Beslutte:
- Funktionen, der definerer projektilets position med hensyn til tid.
- Flyvetid eller tidspunkt, hvor partiklen rammer jorden.
Det er kendt, at accelerationen i en ensartet varieret retlinet bevægelse er en konstant værdi. Dette er tilfældet med projektilstart, hvor accelerationen vil være tyngdekraften
g = - 10 m / sto
Det er også kendt, at accelerationen er det andet afledte af positionen, hvilket indikerer en dobbelt integration i øvelsens opløsning, hvorved der opnås to konstanter af integration.
A (t) = -10
V (t) = ∫A (t) dt = ∫ (-10t) dt = -10t + C1
De første betingelser for øvelsen indikerer, at starthastigheden er V0 = 25 m / s. Dette er hastigheden på tidspunktet t = 0. På denne måde er det tilfreds med:
V (0) = 25 = -10 (0) + C1 Y C1 = 25
Hastighedsfunktionen defineres
V (t) = -10t + 25; Ligheden med MRUV-formlen (VF = V0 + a x t)
På en homolog måde fortsætter vi med at integrere hastighedsfunktionen for at opnå det udtryk, der definerer positionen:
R (t) = ∫V (t) dt = ∫ (-10t + 25) dt = -5tto + 25t + Cto
R (t) = -5tto + 25t + Cto (primitiv position)
Startpositionen R (0) = 30 m er kendt. Derefter beregnes projektilets særlige primitive.
R (0) = 30m = -5 (0)to + 25 (0) + Cto . Hvor Cto = 30
Den første sektion er løst siden R (t) = -5tto + 25t + 30 ; Dette udtryk er homologt med forskydningsformlen i MRUV R (t) = R0 + V0t - gtto/to
For det andet afsnit skal den kvadratiske ligning løses: -5tto + 25t + 30 = 0
Da dette betinger, at partiklen når jorden (position = 0)
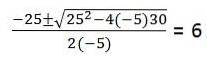
Faktisk giver 2. graders ligning os 2 løsninger T: 6, -1. Værdien t = -1 ignoreres, fordi det er tidsenheder, hvis domæne ikke inkluderer negative tal.
På denne måde løses det andet afsnit, hvor flyvetiden er lig med 6 sekunder.
Eksempel 2
- Find den primitive f (x), der opfylder de oprindelige betingelser:
- f "(x) = 4; f '(2) = 2; f (0) = 7
Med informationen fra det andet afledte f "(x) = 4 begynder antideriveringsprocessen
f '(x) = ∫f "(x) dx
∫4 dx = 4x + C.1
Derefter kender vi tilstanden f '(2) = 2, og fortsætter:
4 (2) + C1 = 2
C1 = -6 og f '(x) = 4x - 8
Fortsæt på samme måde i det andet konstant integration
f (x) = ∫f '(x) dx
∫ (4x - 8) dx = 2xto - 8x + Cto
Den oprindelige betingelse f (0) = 7 er kendt, og vi fortsætter:
2 (0)to - 8 (0) + Cto = 7
Cto = 7 og f (x) = 2xto - 8x + 7
- f "(x) = xto ; f '(0) = 6; f (0) = 3
På samme måde som det foregående problem definerer vi de første derivater og den oprindelige funktion ud fra de oprindelige betingelser.
f '(x) = ∫f "(x) dx
∫ (xto) dx = (x3/ 3) + C1
Med betingelsen f '(0) = 6 fortsætter vi:
(03/ 3) + C1 = 6; Hvor1 = 6 og f '(x) = (x3/ 3) + 6
Så det andet konstant integration
f (x) = ∫f '(x) dx
∫ [(x3/ 3) + 6] dx = (x4/ 12) + 6x + Cto
Den oprindelige betingelse f (0) = 3 er kendt, og vi fortsætter:
[(0)4/ 12] + 6 (0) + Cto = 3; Hvorto = 3
Således opnår vi den primitive særlige
f (x) = (x4/ 12) + 6x + 3
Eksempel 3
- Definer de primitive funktioner givet derivaterne og et punkt på grafen:
- dy / dx = 2x - 2, der passerer gennem punktet (3, 2)
Det er vigtigt at huske, at derivater henviser til linjens hældning, der tangerer kurven på et givet punkt. Hvor det ikke er korrekt at antage, at grafen for derivatet berører det angivne punkt, da dette hører til grafen for den primitive funktion.
På denne måde udtrykker vi differentialligningen som følger:
dy = (2x - 2) dx ; så når vi anvender anti-derivationskriterierne har vi:
∫dy = ∫ (2x - 2) dx
y = xto - 2x + C
Anvendelse af den oprindelige tilstand:
2 = (3)to - 2 (3) + C
C = -1
Opnås: f (x) = xto - 2x - 1
- dy / dx = 3xto - 1 Hvad der passerer gennem punktet (0, 2)
Vi udtrykker differentialligningen som følger:
dy = (3xto - 1) dx ; så når vi anvender anti-derivationskriterierne har vi:
∫dy = ∫ (3xto - 1) dx
y = x3 - x + C
Anvendelse af den oprindelige tilstand:
2 = (0)to - 2 (0) + C
C = 2
Opnås: f (x) = x3 - x + 2
Foreslåede øvelser
Øvelse 1
- Find den primitive f (x), der opfylder de oprindelige betingelser:
- f "(x) = x; f '(3) = 1; f (2) = 5
- f "(x) = x + 1; f '(2) = 2; f (0) = 1
- f "(x) = 1; f '(2) = 3; f (1) = 10
- f "(x) = -x; f '(5) = 1; f (1) = -8
Øvelse 2
- En ballon, der stiger op med en hastighed på 16 ft / s, falder en pose sand fra en højde på 64 ft over jordoverfladen.
- Definer flyvetiden
- Hvad vil vektoren VF når jeg rammer gulvet?
Øvelse 3
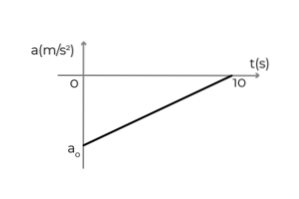
- Figuren viser accelerationstidsgrafen for en bil, der bevæger sig i den positive retning af x-aksen. Bilen kørte med en konstant hastighed på 54 km / t, da føreren trak bremserne for at stoppe på 10 sekunder. Bestemme:
- Den første acceleration af bilen
- Bilens hastighed ved t = 5s
- Forskydning af bilen under bremsning
Øvelse 4
- Definer de primitive funktioner givet derivaterne og et punkt på grafen:
- dy / dx = x, der passerer gennem punktet (-1, 4)
- dy / dx = -xto + 1 Hvad der passerer gennem punktet (0, 0)
- dy / dx = -x + 1, der passerer gennem punktet (-2, 2)
Referencer
- Integreret beregning. De ubestemte integral- og integrationsmetoder. Wilson, Velásquez Bastidas. Magdalena University 2014
- Stewart, J. (2001). Beregning af en variabel. Tidlige transcendentals. Mexico: Thomson Learning.
- Jiménez, R. (2011). Matematik VI. Integreret beregning. Mexico: Pearson Education.
- Fysik I. Mc Graw bakke


Endnu ingen kommentarer