
Kvadrilaterale elementer, egenskaber, klassifikation, eksempler
EN firkant er en polygon med fire sider og fire hjørner. Deres modsatte sider er dem, der ikke har fælles hjørner, mens de er på hinanden følgende sider dem med et fælles toppunkt.
I en firkant er de tilstødende vinkler dem, der deler en side, mens modsatte vinkler de har ingen sider til fælles. Et andet vigtigt kendetegn ved en firkant er, at summen af dens fire indre vinkler er det dobbelte af planens vinkel, dvs. 360 ° eller 2π radianer.
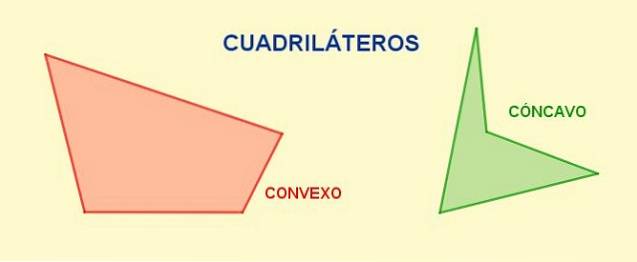
Diagonaler er de segmenter, der forbinder et toppunkt med dets modsatte og i en given firkant kan der fra hvert toppunkt tegnes en enkelt diagonal. Det samlede antal diagonaler i en firkant er to.
Kvadrilaterale figurer er kendt af menneskeheden siden oldtiden. De arkæologiske optegnelser såvel som de konstruktioner, der overlever i dag, vidner om dette..
Ligeledes har firsidene i dag fortsat en vigtig tilstedeværelse i alles hverdag. Læseren kan finde denne form på skærmen, hvor teksten læses lige nu, på vinduer, døre, bildele og utallige andre steder..
Artikelindeks
- 1 Klassificering af firkanter
- 1.1 Typer af parallelogram
- 2 Trapesformet
- 2.1 Typer af trapezider
- 3 Parallelogram
- 3.1 Område af et parallelogram
- 3.2 Diagonaler af et parallelogram
- 3.3 Loven om parallelogrammer
- 4 rektangel
- 4.1 Diagonaler af et rektangel
- 5 Firkant
- 6 Rhombus
- 7 eksempler
- 7.1 Eksempel 1
- 7.2 Eksempel 2
- 7.3 Eksempel 3
- 8 Øvelser løst
- 8.1 - Øvelse 1
- 8.2 - Øvelse 2
- 9 Referencer
Kvadrilateral klassifikation
I henhold til paralleliteten mellem de modsatte sider klassificeres firsidene som følger:
- Trapesformet, når der ikke er nogen parallelisme, og firsidet er konveks.
- Trapes, når der er parallelitet mellem et enkelt par modsatte sider.
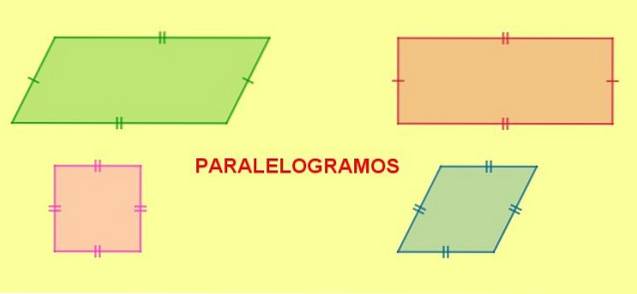
- Parallelogram, når dens modsatte sider er parallelle to og to.
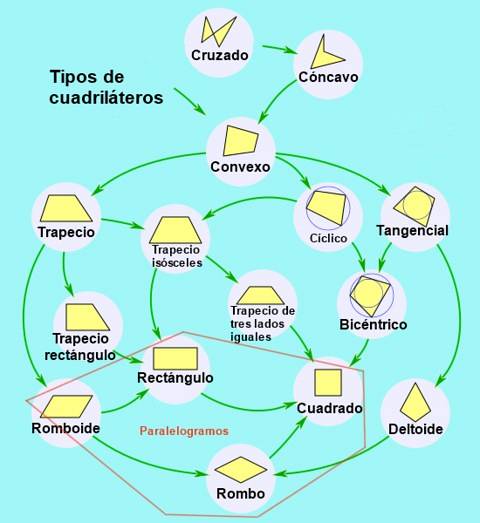
Typer af parallelogram
Til gengæld kan parallelogrammer klassificeres i henhold til deres vinkler og sider som følger:
- Rektangel, er parallelogrammet, der har sine fire indre vinkler med lige mål. De indvendige vinkler af et rektangel danner en ret vinkel (90º).
- Firkant, er et rektangel med sine fire sider af lige mål.
- Diamant, er parallelogrammet med sine fire lige sider, men forskellige tilstødende vinkler.
- Rhomboid, parallelogram med forskellige tilstødende vinkler.
Trapes
Trapesformet er en konveks firkant med to parallelle sider.
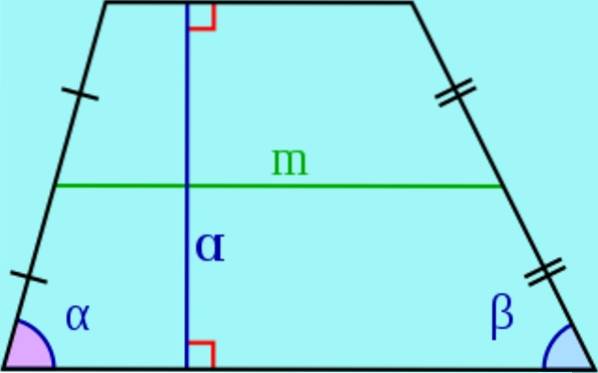
- I en trapez kaldes de parallelle sider baser og de ikke-paralleller kaldes tværgående.
- Det højde af en trapezform er afstanden mellem de to baser, dvs. længden af et segment med ender ved baserne og vinkelret på dem. Dette segment kaldes også en trapezhøjde..
- Det median er det segment, der slutter sig til midtpunkterne for lateralerne. Det kan vises, at medianen er parallel med trapezens baser, og dens længde er lig med halvsummen af baserne.
- Arealet af en trapezoid er dens højde ganget med halvsummen af baserne:
Areal af en trapezform = højde * (base 1 + base 2) / 2
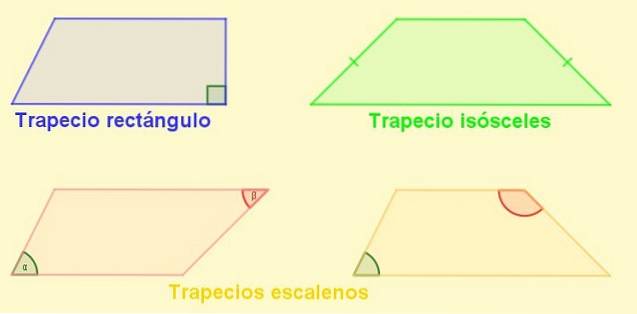
Typer af trapezoider
-Rektangel trapesformet: Er den med en lateral vinkelret på baserne. Denne laterale er også trapesens højde.
-Trapezium ligebenede: Den med lige lange sider. I en ligeben trapezform er vinklerne ved siden af baserne ens.
-Scalene trapez: Den ene med siderne i forskellige længder. Dens modsatte vinkler kan være en akut og den anden stump, men det kan også ske, at begge er stumpe eller begge er akutte..
Parallelogram
Parallellogrammet er en firkant, hvis modsatte sider er parallelle to og to. I et parallelogram er de modsatte vinkler ens, og de tilstødende vinkler er supplerende, eller med andre ord, de tilstødende vinkler tilføjes op til 180º.
Hvis et parallelogram har en ret vinkel, vil alle andre vinkler også være, og den resulterende figur kaldes rektangel. Men hvis rektanglet også har sine tilstødende sider af samme længde, så er alle dets sider ens, og den resulterende figur er a firkant.
Når et parallelogram har to tilstødende sider af samme længde, vil alle siderne have samme længde, og den resulterende figur er a diamant.
Højden på et parallelogram er et segment med ender på sine modsatte sider og vinkelret på dem..
Område af et parallelogram
Arealet af et parallelogram er produktet af basen gange dens højde, idet basen er en side vinkelret på højden (figur 6).
Areal af et parallelogram = bund x højde = a. h
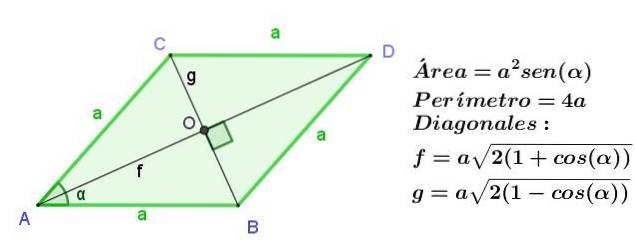
Diagonaler af et parallelogram
Firkantet af diagonalen, der starter fra et toppunkt, er lig med summen af kvadraterne på de to sider, der støder op til toppunktet plus det dobbelte produkt af disse sider ved cosinus for vinklen på det toppunkt:
Fto = ato + dto + 2 a d Cos (α)
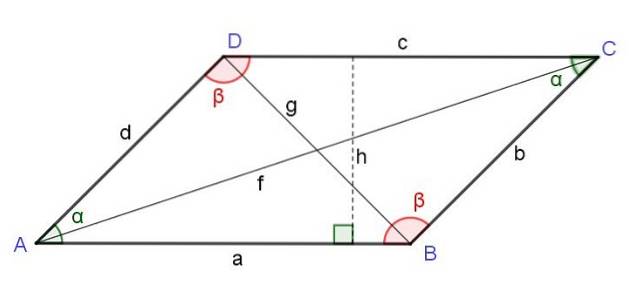
Firkantet af diagonalen modsat toppunktet af et parallelogram er lig med summen af kvadraterne på de to sider ved siden af toppunktet og fratrækker det dobbelte produkt af disse sider ved cosinus af vinklen på det øverste punkt:
gto = ato + dto - 2 a d Cos (α)
Lov om parallelogrammer
I ethvert parallelogram er summen af kvadraterne på dens sider lig med summen af kvadraterne på diagonalerne:
tilto + bto + cto + dto = fto + gto
Rerøre sammen
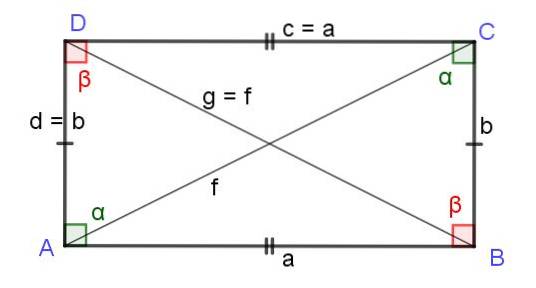
Rektanglet er en firkant med dets modsatte sider parallelt to og to, og som også har en ret vinkel. Med andre ord er rektanglet en type parallelogram med en ret vinkel. For at være parallelogram, rektanglet har modsatte sider af samme længde a = c og b = d.
Men som i ethvert parallelogram er de tilstødende vinkler supplerende og de modsatte vinkler ens, i rektanglet, fordi det har en ret vinkel, vil det nødvendigvis danne lige vinkler i de andre tre vinkler. Nemlig i et rektangel måler alle indvendige vinkler 90º eller π / 2 radianer.
Diagonaler af et rektangel
I et rektangel er diagonalerne af samme længde, som det vil blive demonstreret nedenfor. Begrundelsen er som følger: Et rektangel er et parallelogram med alle dets rette vinkler og arver derfor alle egenskaberne ved parallelogrammet, inklusive formlen, der giver diagonalernes længde:
Fto = ato+ dto + 2 a d Cos (α)
gto = ato + dto - 2 a d Cos (α)
med α = 90º
Hvad Cos (90º) = 0, så sker det, at:
Fto = gto = ato + dto
Det er f = g, og derfor længderne F Y g af de to diagonaler i rektanglet er ens, og deres længde er givet ved:
Diagonaler længde af et rektangel = √ (ato + bto)
Også hvis det er i et rektangel med tilstødende sider til Y b den ene side tages som basen, den anden side vil være i højden, og arealet af rektanglet vil derfor være:
Areal af rektanglet = a x b.
Omkredsen er summen af alle siderne af rektanglet, men da modsætningerne er ens, følger det, at for et rektangel med sider til Y b omkredsen er givet med følgende formel:
Rektangelets omkreds = 2 (a + b)
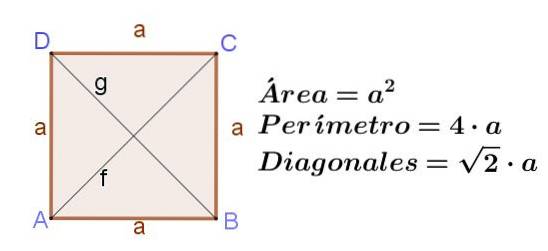
Firkant
Firkanten er et rektangel med tilstødende sider af samme længde. Hvis pladsen har en side til, derefter dens diagonaler F Y g har samme længde, hvilket er f = g = (√2) a.
Arealet af en firkant er dens side i firkant:
Areal af en firkant = ato
Omkredsen af en firkant er to gange siden:
Omkreds af en firkant = 4 a
Diamant
Rhombus er et parallelogram med dets tilstødende sider af samme længde, men som i et parallelogram er de modsatte sider lige så, alle sider af en rombe er ens i længden.
Diagonalerne på en rombe er af forskellig længde, men skærer sig vinkelret.
Eksempler
Eksempel 1
Vis at de indre vinkler i en firkant (ikke krydset) er 360 °.
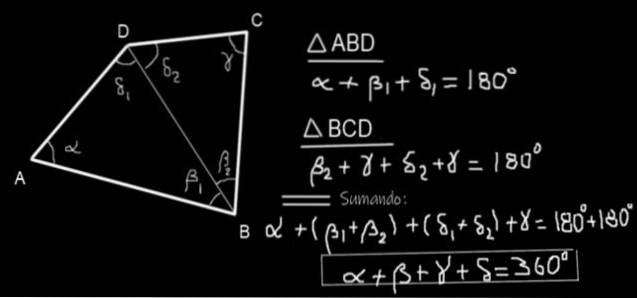
En firkantet ABCD overvejes (se figur 10), og den diagonale BD tegnes. To trekanter ABD og BCD dannes. Summen af de indvendige vinkler af trekanten ABD er:
α + β1 + δ1 = 180º
Og summen af de indre vinkler af trekanten BCD er:
β2 + y + δto = 180º
Tilføjelse af de to ligninger, vi opnår:
α + β1 + δ1 + βto + y + δto = 180º + 180º
Gruppering:
α + (β1 + βto) + (δ1 + δto) + γ = 2 * 180 °
Ved at gruppere og omdøbe vises det endelig at:
α + β + δ + γ = 360 °
Eksempel 2
Vis, at medianen af en trapezoid er parallel med dens baser, og dens længde er semisummen af baserne.
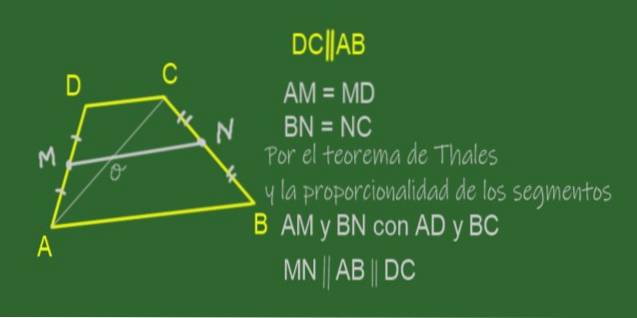
Medianen af en trapez er det segment, der forbinder midtpunkterne på dets sider, det vil sige de ikke-parallelle sider. I trapesformet ABCD vist i figur 11 er medianen MN.
Da M er midtpunktet for AD, og N er midtpunktet for BC, er det sandt, at forholdet AM / AD og BN / BC er ens.
Det vil sige, at AM er proportional med BN i den samme andel, som AD er til BC, så betingelserne er givet for anvendelsen af Thales '(gensidige) sætning, der siger følgende:
"Hvis proportionale segmenter bestemmes i tre eller flere linjer skåret af to sekanter, er disse linjer alle parallelle".
I vores tilfælde konkluderes det, at linjerne MN, AB og DC er parallelle med hinanden, derfor:
"Lmedianen af en trapez er parallel med dens baser".
Nu vil Thales sætning blive anvendt:
"Et sæt paralleller skåret af to eller flere sekanter bestemmer proportionale segmenter".
I vores tilfælde AD = 2 AM, AC = 2 AO, så trekanten DAC svarer til trekanten MAO, og følgelig DC = 2 MO.
Et lignende argument giver os mulighed for at bekræfte, at CAB svarer til CON, hvor CA = 2 CO og CB = 2 CN. Det følger straks, at AB = 2 ON.
Kort sagt, AB = 2 ON og DC = 2 MO. Så når vi tilføjer, har vi:
AB + DC = 2 ON + 2 MO = 2 (MO + ON) = 2 MN
Endelig er MN ryddet:
MN = (AB + DC) / 2
Og det konkluderes, at medianen af en trapez måler halvsummen af baserne eller med andre ord: medianen måler summen af baserne divideret med to.
Eksempel 3
Vis at diagonaler krydser hinanden i en vinkel i en rombe.

Tavlen i figur 12 viser den nødvendige konstruktion. Først tegnes parallelogrammet ABCD med AB = BC, det vil sige en rombe. Diagonaler AC og DB bestemmer otte vinkler vist i figuren.
Ved hjælp af sætningen (a.i.p.), der siger, at skiftende indvendige vinkler mellem paralleller skåret af en sekant bestemmer lige vinkler, kan vi fastslå følgende:
a1 = γ1, α2 = γ2, δ1 = Β1 og δ2 = β2. (*)
På den anden side, da de tilstødende sider af en rombe har samme længde, bestemmes fire ligebenede trekanter:
DAB, BCD, CDA og ABC
Nu påberåbes trekanten (ligebenede) sætning, som siger, at vinklerne ved siden af basen er lige store, hvorfra det konkluderes, at:
δ1 = β2, δ2 = β1, α2 = γ1 og α1 = γ2 (**)
Hvis forholdet (*) og (**) kombineres, opnås følgende vinkellighed:
a1 = α2 = γ1 = γ1 på den ene side og β1 = Β2 = δ1 = δ2 på den anden.
Når vi minder om ligestillingssætningen, der siger, at to trekanter med en lige side mellem to lige store vinkler er ens, har vi:
AOD = AOB og dermed også vinklerne ∡AOD = ∡AOB.
Derefter ∡AOD + ∡AOB = 180º, men da begge vinkler er lige store, har vi 2 ∡AOD = 180º hvilket betyder at ∡AOD = 90º.
Det vil sige, det er vist geometrisk, at diagonalerne på en rombe krydser hinanden vinkelret.
Øvelser løst
- Øvelse 1
Vis, at de ikke-rigtige vinkler er supplerende i en ret trapez.
Opløsning
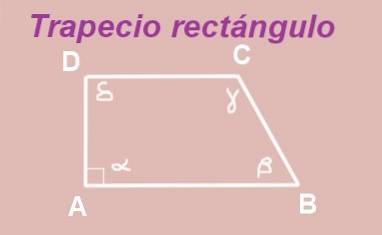
Den trapezformede ABCD er konstrueret med baser AB og DC parallelle. Den indvendige vinkel på toppunkt A er rigtig (den måler 90º), så vi har en højre trapez.
Vinkler α og δ er interne vinkler mellem to paralleller AB og DC, derfor er de ens, det vil sige δ = α = 90º.
På den anden side er det blevet vist, at summen af de firkantede indre vinkler udgør 360 °, det vil sige:
α + β + γ + δ = 90º + β + 90º + δ = 360º.
Ovenstående fører til:
β + δ = 180º
Bekræftelse af, hvad man ønskede at vise, at vinklerne β og δ er supplerende.
- Øvelse 2
Et parallelogram ABCD har AB = 2 cm og AD = 1 cm, derudover er vinklen BAD 30º. Bestem arealet af parallelogrammet og længden af dets to diagonaler.
Opløsning
Arealet af et parallelogram er produktet af længden af dens base gange dens højde. I dette tilfælde tages længden af segmentet b = AB = 2 cm som basis, den anden side har længden a = AD = 1 cm, og højden h beregnes som følger:
h = AD * Sen (30º) = 1 cm * (1/2) = ½ cm.
Så: Areal = b * h = 2 cm * ½ cm = 1 cmto.
Referencer
- C. E. A. (2003). Geometrielementer: med kompasets øvelser og geometri. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematik 2. Grupo Editorial Patria.
- Freed, K. (2007). Opdag polygoner. Benchmark Education Company.
- Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematik Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende udgave). Pearson Uddannelse.
- Patiño, M. (2006). Matematik 5. Redaktionel Progreso.
- Wikipedia. Kvadrilaterale. Gendannet fra: es.wikipedia.com



Endnu ingen kommentarer