Akkordlængde (geometri), sætning og øvelser

EN snor, i plane geometri er det linjesegmentet, der forbinder to punkter på en kurve. Linjen, der indeholder dette segment, siges at være en sekant linje til kurven. Dette er ofte en cirkel, men akkorder kan helt sikkert trækkes på mange andre kurver, såsom ellipser og paraboler..

I figur 1 til venstre er der en kurve, som punkterne A og B. hører til. Akkorden mellem A og B er det grønne segment. Til højre er en omkreds og en af ​​dens strenge, da det er muligt at tegne uendelig.

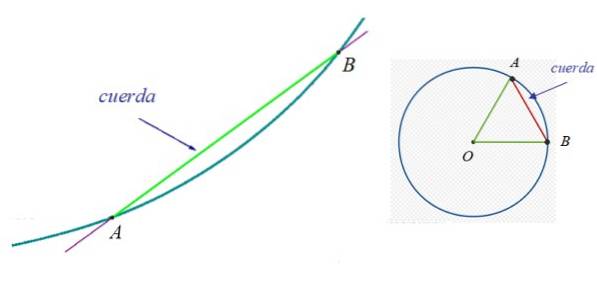
I omkredsen er dens diameter særlig interessant, hvilket også er kendt som større akkord. Det er en akkord, der altid indeholder centrum af omkredsen og måler dobbelt så radien.

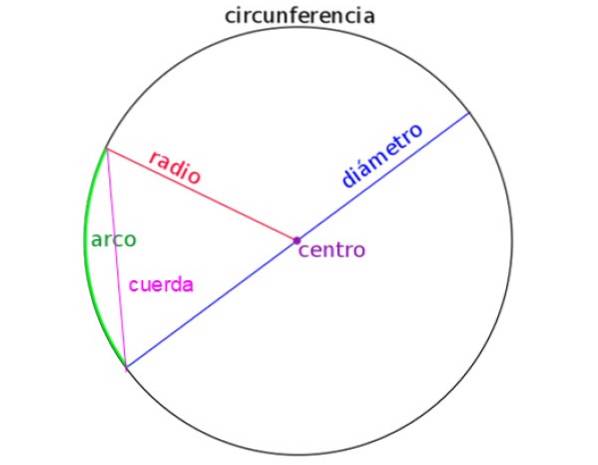
Følgende figur viser radius, diameter, en akkord og også en cirkelbue. Korrekt identifikation af hver enkelt er vigtig, når man løser problemer.

Artikelindeks

• 1 Akkordlængde af en omkreds
  • 1.1 Strengteorem 
• 2 Løst øvelser af strenge
  • 2.1 - Øvelse 1
  • 2.2 - Øvelse 2
• 3 Referencer

Akkordlængde af en omkreds

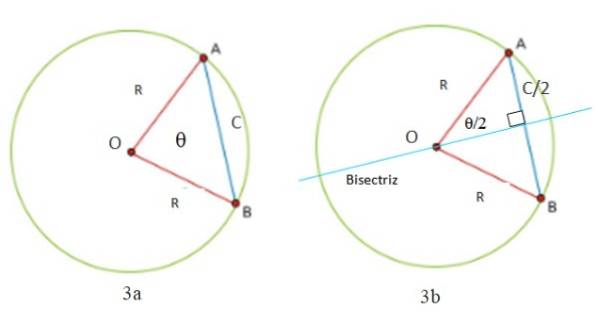
Vi kan beregne akkordlængden i en cirkel fra figur 3a og 3b. Bemærk, at en trekant altid er dannet med to lige sider (ensbenede): segmenterne OA og OB, som måler R, radius af omkredsen. Den tredje side af trekanten er segmentet AB, kaldet C, hvilket er nøjagtigt længden på akkorden.

Det er nødvendigt at tegne en linje vinkelret på akkorden C for at skære den vinkel θ, der findes mellem de to radier, og hvis toppunkt er centrum O for omkredsen. Dette er en central vinkel -fordi dens toppunkt er center- og halveringslinjen er også en sekant for omkredsen.

Umiddelbart dannes to højre trekanter, hvis hypotenus måler R. Da halveringen og med den diameteren deler akkorden i to lige store dele, viser det sig, at det ene ben er halvdelen af ​​C, som vist i figur 3b.

Fra definitionen af ​​sinus i en vinkel:

sin (θ / 2) = modsat ben / hypotenus = (C / 2) / R

Derfor:

sin (θ / 2) = C / 2R

C = 2R sin (θ / 2)

Streng sætning 

Strengteorem går sådan her:

Hvis to akkorder i en cirkel krydser hinanden på et punkt, er produktet af længden af ​​segmenterne, der vises på et af akkorderne, lig med produktet af længderne af segmenterne, der er defineret på det andet akkord..

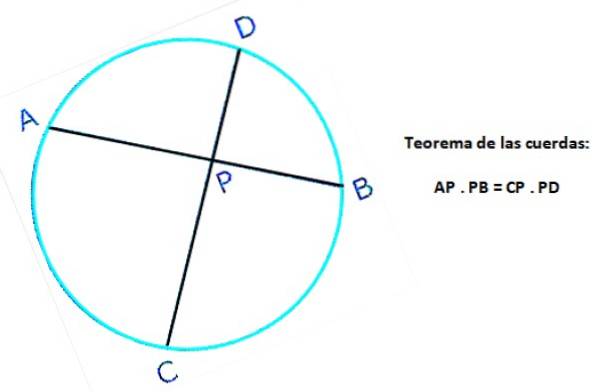
Følgende figur viser to akkorder med samme omkreds: AB og CD, der krydser hinanden ved punkt P. I akkorden AB er segmenterne AP og PB defineret, mens i akkorden er CD CP og PD defineret. Så ifølge sætningen:

AP. PB = CP. P.S.

Løst øvelser af strenge

- Øvelse 1

En omkreds har en 48 cm akkord, som er 7 cm fra midten. Beregn cirkelarealet og omkredsen.

Opløsning  

For at beregne arealet af cirkel A er det nok at kende radius af omkredsen i kvadrat, da det er sandt:

A = π.R^to

Nu er figuren, der er dannet med de leverede data, en ret trekant, hvis ben er henholdsvis 7 og 24 cm.

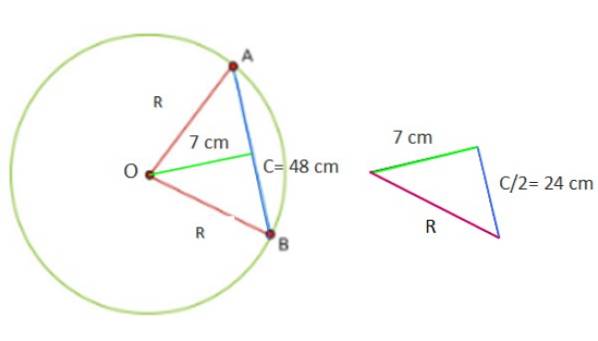
Derfor for at finde værdien af ​​R^to Pythagoras sætning anvendes direkte c^to = a^to + b^to, da R er hypotenusen i trekanten:

R^to = (7 cm)^to + (24 cm)^to = 625 cm^to

Så det ønskede område er:

A = π. 625 cm^to = 1963,5 cm^to

Med hensyn til omkredsen eller længden L af omkredsen beregnes den ved:

L = 2π. R

Erstatning af værdier:

R = √625 cm^to = 25 cm

L = 2π. 25 cm = 157,1 cm.

- Øvelse 2

Bestem længden af ​​akkorden til en cirkel, hvis ligning er:

x^to + Y^to - 6x - 14y -111 = 0

Koordinaterne for akkordets midtpunkt er kendt for at være P (17/2; 7/2).

Opløsning

Akkordets midtpunkt P ikke hører til omkredsen, men akkordens slutpunkter gør det. Problemet kan løses ved hjælp af den tidligere angivne streng sætning, men først er det praktisk at skrive ligningen af ​​omkredsen i kanonisk form for at bestemme dens radius R og dens centrum O.

Trin 1: Få den kanoniske ligning af omkredsen

Den kanoniske ligning af cirklen med centrum (h, k) er:

(x-h)^to + (y-k)^to = R^to

For at opnå det er det nødvendigt at udfylde firkanter:

(x^to - 6x) + (og^to - 14y) -111 = 0

Bemærk, at 6x = 2. (3x) og 14y = 2. (7y), så det forrige udtryk omskrives sådan og forbliver uændret:

(x^to - 6x + 3^to-3^to) + (og^to - 14 år + 7^to-7^to) -111 = 0

Og nu husker vi definitionen af ​​bemærkelsesværdigt produkt (a-b)^to = a^to - 2ab + b^to Det kan skrives:

(x - 3)^to - 3^to + (og - 7)^to - 7^to - 111 = 0

= (x - 3)^to + (og - 7)^to = 111 + 3^to + 7^to → (x - 3)^to + (og - 7)^to = 169

Omkredsen har center (3,7) og radius R = √169 = 13. Følgende figur viser grafen for omkredsen og de akkorder, der skal bruges i sætningen:

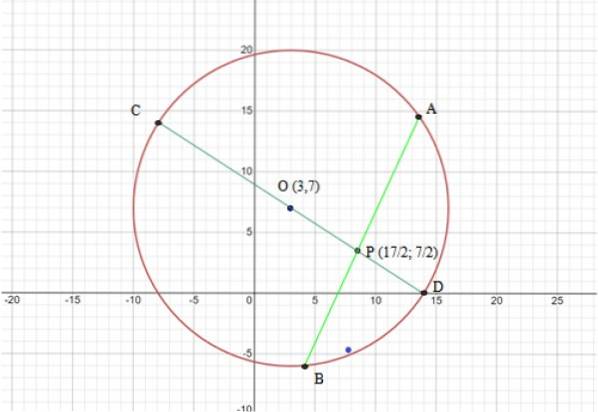
Trin 2: Bestem de segmenter, der skal bruges i strengteoremet

De anvendte segmenter er CD- og AB-strenge, ifølge figur 6 er begge skåret i punkt P, derfor:

CP. PD = AP. PB

Nu skal vi finde afstanden mellem punkterne O og P, da dette giver os længden af ​​segmentet OP. Hvis vi tilføjer radius til denne længde, har vi segmentet CP.

Afstanden d_OP mellem to koordinatpunkter (x₁,Y₁) og (x_to,Y_to) det er:

d_OP^to = OP^to = (x_to - x₁)^to + (Y_to - Y₁)^to = (3- 17/2)^to + (7/7/2)^to = 121/4 + 49/4 = 170/4

d_OP = OP = √170 / 2

Med alle de opnåede resultater plus grafen konstruerer vi følgende liste over segmenter (se figur 6):

CO = 13 cm = R

OP = √170 / 2 cm

CP = OP + R = 13 + √170 / 2 cm

PD = OD - OP = 13 - √170 / 2 cm

AP = PB

2.AP = akkordlængde

Udskiftning i strengteoremet:

CP. PD = AP. PB = [(13 + √170 / 2). (13 -√170 / 2)] = AP^to

[169 -170/4] = AP^to

253/2 = AP^to

AP = √ (253/2)

Akkordens længde er 2.AP = 2 (√253 / 2) = √506

Kunne læseren løse problemet på en anden måde?

Referencer

1. Baldor, A. 2004. Plane- og rumgeometri med trigonometri. Publicaciones Cultural S.A. de C.V. Mexico.
2. C-K12. Akkordens længde. Gendannet fra: ck12.org.
3. Escobar, J. The Circumference. Gendannet fra: matematicas.udea.edu.co.
4. Villena, M. Cónicas. Gendannet fra: dspace.espol.edu.ec.
5. Wikipedia. Reb (geometri). Gendannet fra: es.wikipedia.org.