
Hvad er kanten af en terning?
Det kanten af en terning Det er en kant af det: det er linjen, der forbinder to hjørner eller hjørner. En kant er den linje, hvor to flader af en geometrisk figur krydser hinanden.
Ovenstående definition er generel og gælder for enhver geometrisk figur, ikke kun terningen. Når det er en flad figur, svarer kanterne til siderne af figuren.

Parallelepiped kaldes en geometrisk figur med seks ansigter i form af parallelogrammer, hvoraf de modsatte er lige og parallelle..
I det særlige tilfælde, hvor ansigterne er firkantede, kaldes parallelepiped en terning eller hexahedron, en figur, der betragtes som en almindelig polyhedron..
Måder til at identificere kanterne på en terning
For en bedre illustration kan hverdagsgenstande bruges til at bestemme præcist, hvad en ternings kanter er.
1- Samling af en papirterning
Hvis du ser på, hvordan en papir- eller papterning er bygget, kan du se, hvad dens kanter er. Du starter med at tegne et kryds som det i figuren og markere bestemte linjer indeni.
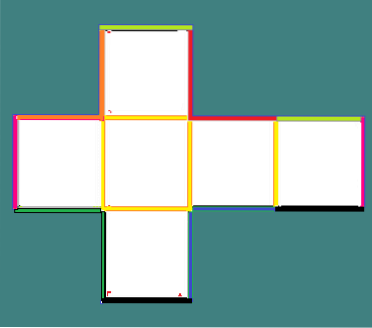
Hver af de gule linjer repræsenterer en fold, som vil være en kant af terningen (kanten).
Tilsvarende vil hvert par linjer, der har den samme farve, danne en kant, når de sammenføjes. I alt har en terning 12 kanter.
2- Tegning af en terning
En anden måde at se, hvad en ternings kanter er, er at observere, hvordan den tegnes. Vi begynder med at tegne en firkant med side L; hver side af firkanten er en kant af terningen.
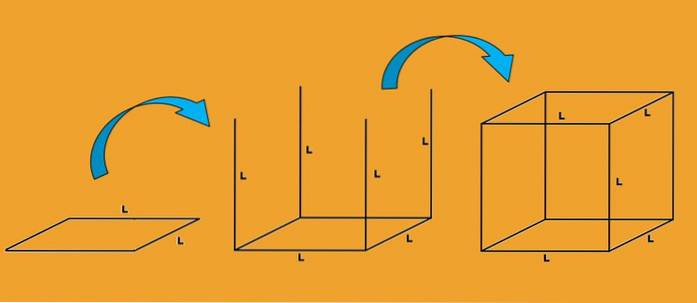
Derefter tegnes fire lodrette linjer fra hvert toppunkt, og længden af hver af disse linjer er L. Hver linje er også en kant af terningen.
Endelig tegnes en anden firkant med side L, således at dens hjørner falder sammen med enden af kanterne tegnet i det foregående trin. Hver af siderne på denne nye firkant er en kant af terningen.
3- Rubiks terning
For at illustrere den geometriske definition, der blev givet i starten, kan du se på en Rubiks terning.

Hvert ansigt har forskellige farver. Kanterne er repræsenteret af den linje, hvor ansigterne med forskellige farver krydser hinanden.
Eulers sætning
Eulers sætning for polyeder siger, at givet en flerhed er antallet af ansigter C plus antallet af hjørner V lig med antallet af kanter A plus 2. Det vil sige C + V = A + 2.
På de foregående billeder kan du se, at en terning har 6 ansigter, 8 hjørner og 12 kanter. Derfor opfylder den Eulers sætning for polyeder, da 6 + 8 = 12 + 2.
At kende længden af en kant på en terning er meget nyttigt. Hvis længden af en kant er kendt, er længden af alle dens kanter kendt, hvormed visse data fra terningen kan opnås, såsom dens volumen.
Volumenet af en terning er defineret som L³, hvor L er længden af dens kanter. Derfor er det kun nødvendigt at kende værdien af L for at kende kubens volumen.
Referencer
- Guibert, A., Lebeaume, J., & Mousset, R. (1993). Geometriske aktiviteter til spædbørn og grundskoleundervisning: til spædbørn og grundskoleundervisning. Narcea Editions.
- Itzcovich, H. (2002). Studiet af figurer og geometriske kroppe: aktiviteter i de første år af skolegang. Noveduc Books.
- Rendon, A. (2004). AKTIVITETER NOTEBOOK 3 2. HIGH SCHOOL. Redaktionel Tebar.
- Schmidt, R. (1993). Beskrivende geometri med stereoskopiske figurer. Vend tilbage.
- Spektrum (red.). (2013). Geometri, klasse 5. Carson-Dellosa Publishing.


Endnu ingen kommentarer