Det kalibreringskurve Det er en graf, der relaterer to variabler, som bruges til at verificere, at et måleudstyr fungerer korrekt. Uanset udstyr påvirker tid, brug og naturligt slid kvaliteten af målingen.
Derfor er det vigtigt regelmæssigt at kontrollere, at den fungerer korrekt. Dette gøres ved at sammenligne målingerne fra udstyret med målingerne fra en standardindretning, der bruges som reference. Dette referenceudstyr er det mest nøjagtige.
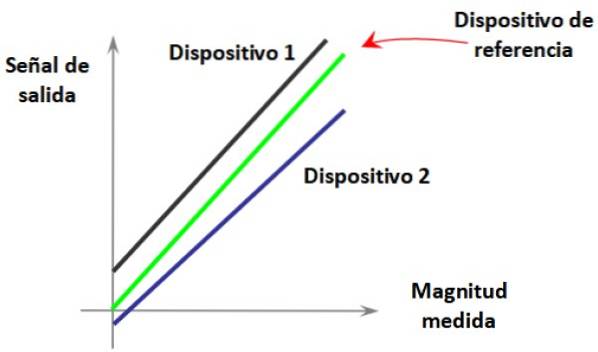
For eksempel har vi i figur 1 udgangssignalet fra en ideel enhed i grønt sammenlignet med den målte størrelse, begge er proportionale.
I samme graf er kurverne for to forskellige instrumenter, der ikke er kalibreret, og som har lidt forskellige adfærd fra hinanden og fra standarden.
Artikelindeks
Antag for eksempel, at vi ønsker at kalibrere et dynamometer, som er en enhed, der bruges til at måle kræfter såsom vægten af objekter og dem, der vises, når et objekt accelereres..
For at få en fjeder til at strække sig er det nødvendigt at anvende en kraft, der er proportional med strækningen, ifølge Hookes lov.
Et simpelt dynamometer består af en fjeder inde i et rør udstyret med en markør og en skala for at indikere strækning. I den ene ende er der en ring til at holde dynamometeret og i den anden en krog til at hænge vægte.
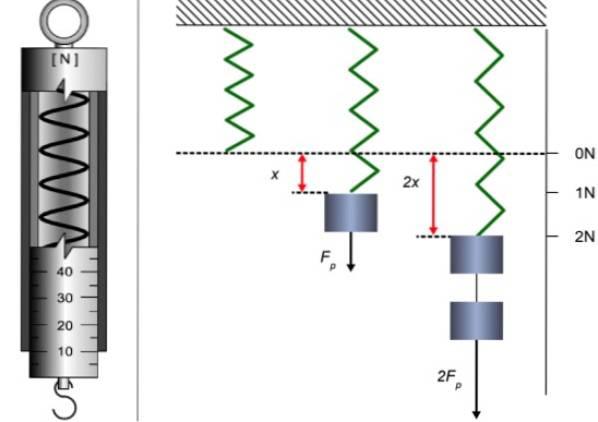
En måde at kalibrere dynamometeret på er ved at hænge forskellige vægte, hvis masse tidligere blev bestemt med en balance (referenceinstrumentet) og måle fjederens strækning eller forlængelse, som formodes at være lys..
Hookes lov anvendt på fjedermassesystemet i statisk ligevægt resulterer i følgende ligning, der relaterer fjederlængden til den hængende masse:
L = (g / k) m + Lo
Hvor:
-L: fjederens samlede længde
-g: tyngdeacceleration
-k: konstant fjeder
-m: masse
-Lo: naturlig fjederlængde.
Når du har flere par punkter længde-masse, de plottes derefter for at konstruere kalibreringskurven. Da forholdet mellem længde L og masse m er lineært, er kurven en lige linje, hvor:
Hældning = g / k
Dette er trinene til at lave en kalibreringskurve til et måleinstrument.
Vælg den sammenligningsstandard, der skal bruges, i henhold til den enhed, der skal kalibreres.
Vælg det relevante område af værdier, og bestem det optimale antal målinger, der skal udføres. Hvis vi kalibrerer et dynamometer, bliver vi først nødt til at vurdere grænsen for den vægt, der kan hænges, uden at den deformeres permanent. Hvis dette skulle ske, ville instrumentet være ubrugeligt.
Tag par aflæsninger: den ene er aflæsningen foretaget med standardmønsteret, den anden er målingen foretaget med sensoren, der kalibreres.
Lav en graf over de par aflæsninger, der er opnået i det foregående trin. Det kan gøres manuelt, på grafpapir eller ved hjælp af et regneark.
Den sidstnævnte mulighed foretrækkes, da sporing i hånden kan føre til lette unøjagtigheder, mens en bedre pasform kan opnås med regnearket..
Kalibreringskurver bruges også til at konvertere en mængde til en anden, der er let at læse, gennem en ejendom eller lov, der relaterer dem..
Et alternativ til brugen af kviksølv er elektrisk modstand. Modstand er en god termometrisk egenskab, da den varierer med temperaturen og også er let at måle med et ohmmeter eller amperemeter..
Nå, i dette tilfælde ville en passende standard til at konstruere kalibreringskurven være et godt laboratorietermometer..
Du kan måle temperatur - modstandspar og tage dem til en graf, som senere vil blive brugt til at bestemme enhver temperaturværdi, der kender modstanden, så længe værdien af dette er inden for det måleområde, der er blevet taget.
Den følgende kalibreringskurve viser temperaturen på x-aksen med standardtermometeret og temperaturen på den lodrette akse med et platinmodstandstermometer, kaldet termometer A.
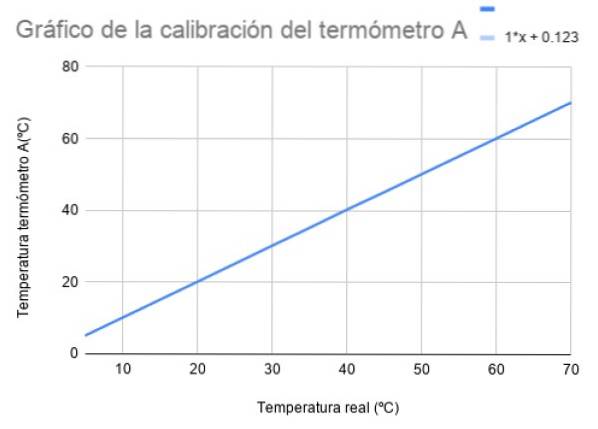
Regnearket finder den linje, der bedst passer til målingerne, hvis ligning vises øverst til højre. Platintermometeret har en drift på 0,123 ºC i forhold til standarden.
Det er en metode, der anvendes i analytisk kemi og består af en referencekurve, hvor den målte størrelse er koncentrationen af en analyt på den vandrette akse, mens den instrumentelle respons vises på den lodrette akse, som vist i det følgende eksempel.
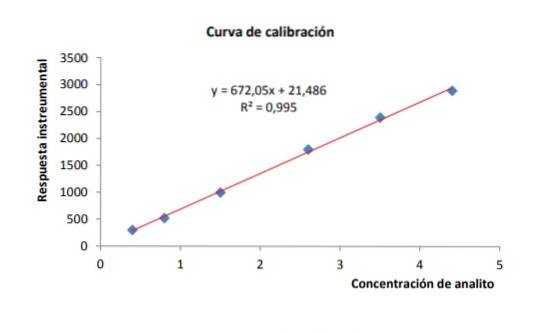
Kurven bruges til ved interpolation at finde koncentrationen af analyt til stede i en ukendt prøve gennem instrumental respons..
Den instrumentelle respons kan være en elektrisk strøm eller en spænding. Begge mængder er lette at måle i laboratoriet. Kurven bruges derefter til at finde ud af koncentrationen af den ukendte analyt på denne måde:
Antag, at strømmen er 1500 mA på kalibreringskurven. Vi står på dette punkt på den lodrette akse og tegner en vandret linje op til kurven. Fra dette punkt projicerer vi en linje lodret mod x-aksen, hvor den respektive koncentration af analyt læses..
Konstruer kalibreringskurven for en fjeder med elastisk konstant k og ud fra diagrammet bestemme værdien af den konstante, alt baseret på følgende eksperimentelle data om længde - massepar:
Hvert par værdier fortolkes som følger:
Når en 1 kg masse hænges, strækkes fjederen til 0,32 m. Hvis en 2 kg masse hænges, måler fjederen 0,40 m og så videre.
Ved hjælp af et regneark uddybes grafen over længde versus masse, hvilket viser sig at være en lige linje som forventet fra Hookes lov, da forholdet mellem længde L og masse m er givet ved:
L = (g / k) m + Lo
Som forklaret i tidligere afsnit. Grafen, der opnås, er følgende:
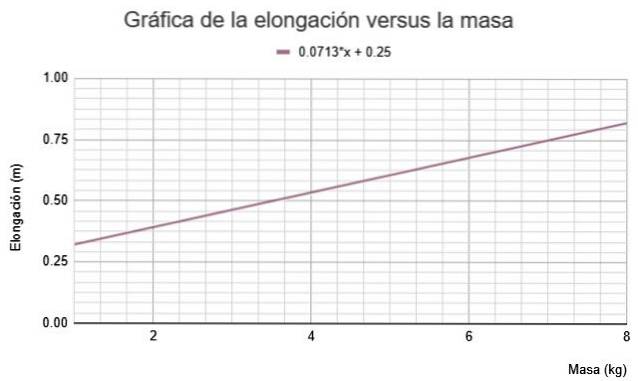
Under titlen viser regnearket ligningen for den linje, der bedst passer til de eksperimentelle data:
L = 0,0713 m + 0,25
Linjens afskæring med den lodrette akse er fjederens naturlige længde:
Leller = 0,25 m
På sin side er hældningen kvotienten g / k:
g / k = 0,0713
Derfor tager g = 9,8 m / sto, værdien af fjederkonstanten er:
k = (9,8 / 0,0713) N / m
k = 137,45 N / m
Med denne værdi er vores fjeder kalibreret, og dynamometeret er klar til at måle kræfter på følgende måde: en ukendt masse hænges, der producerer en bestemt strækning, der læses på den lodrette akse..
Fra denne værdi trækkes en vandret linje, indtil den når kurven, og på det tidspunkt projiceres en lodret linje til x-aksen, hvor massens værdi læses. Når vi tager massen, har vi dens vægt, hvilket er den kraft, der forårsager forlængelsen.
Endnu ingen kommentarer