
Afledt af cotangentberegning, bevis, øvelser
Det derivat af cotangenten er lig med det modsatte af kvadratet af cosecanten "-Cscto”. Denne formel overholder de afledte love pr. Definition og differentieringen af trigonometriske funktioner. Det betegnes som følger:
d (ctg u) = -cscto eller. du
Hvor "du" symboliserer udtrykket afledt af argumentfunktionen med hensyn til den uafhængige variabel.

Artikelindeks
- 1 Hvordan beregnes det?
- 2 Karakteristika for cotangentfunktionen
- 2.1 Lodrette asymptoter
- 2.2 Domæne
- 2.3 Rækkevidde
- 2.4 Frekvens
- 2.5 Adfærd
- 3 Demo
- 3.1 Trigonometrisk differenstæt
- 3.2 Bevis pr. Definition af derivat
- 4 Løst øvelser
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referencer
Hvordan beregnes det?
Proceduren til at udvikle disse derivater er ret enkel. Alt du skal gøre er korrekt at identificere argumentet og den type funktion, det repræsenterer..
Eksempelvis har udtrykket Ctg (f / g) en division i sit argument. Dette vil kræve en differentiering med hensyn til U / V efter udvikling af derivatet af cotangenten.
Cotangenten er den gensidige af tangenten. Algebraisk betyder dette, at:
(1 / tg x) = ctg x
Ctg x = Cos x / Sen x
Det er forkert at sige, at cotangentfunktionen er den "inverse" af tangenten. Dette skyldes, at den inverse tangentfunktion pr. Definition er buetangens.
(Tg-1 x) = arctg x
Ifølge Pythagoras trigonometri er cotangenten involveret i følgende afsnit:
Ctg x = (cos x) / (sin x)
Ctgto x + 1 = Cscto x
Ifølge analytisk trigonometri reagerer den på følgende identiteter:
Ctg (a + b) = (1 - tg a. Tg b) / (tg a + tg b)
Ctg (a - b) = (1 + tg a. Tg b) / (tg a - tg b)
Ctg (2a) = (1 - tgto a) / (2tg a)
Karakteristika for cotangent-funktionen
Det er nødvendigt at analysere forskellige egenskaber ved funktionen f (x) = ctg x for at definere de aspekter, der er nødvendige for at undersøge dens differentierbarhed og anvendelse.
Lodrette asymptoter
Funktionen cotangent er ikke defineret på de værdier, der gør udtrykket "Senx" nul. På grund af dets ækvivalente Ctg x = (cos x) / (sin x) vil den have en ubestemmelighed i alle "nπ" med n tilhørende heltalene.
Det vil sige, at i hver af disse værdier på x = nπ vil der være en lodret asymptote. Når du nærmer dig fra venstre, falder cotangentens værdi hurtigt, og når du nærmer dig fra højre, stiger funktionen på ubestemt tid.
Domæne
Domænet for den cotangente funktion udtrykkes med sættet x ∈ R / x ≠ nπ, n ∈ Z. Dette læses som "x tilhører sættet med reelle tal, således at x er forskellig fra nπ, hvor n hører til sættet med heltal".
Rang
Området for den cotangente funktion er fra minus til plus uendelig. Derfor kan det konkluderes, at dens rækkevidde er sættet med reelle tal R.
Frekvens
Den cotangente funktion er periodisk og dens periode er lig med π. På denne måde er ligestillingen Ctg x = Ctg (x + nπ) opfyldt, hvor n hører til Z.
Opførsel
Det er en ulige funktion, da Ctg (-x) = - Ctg x. På denne måde er det kendt, at funktionen præsenterer en symmetri med hensyn til koordinatets oprindelse. Det præsenterer også et fald i hvert interval placeret mellem 2 på hinanden følgende lodrette asymptoter.
Det har ikke maksimale eller minimale værdier, fordi dets tilnærmelser til de lodrette asymptoter præsenterer adfærd, hvor funktionen øges eller falder på ubestemt tid.
Nullerne eller rødderne til cotangentfunktionen findes ved ulige multipla af π / 2. Dette betyder, at Ctg x = 0 gælder for værdier i formen x = nπ / 2 med n ulige heltal.
Demonstration
Der er 2 måder at bevise afledningen af den cotangente funktion.
Trigonometrisk differenstæt
Afledningen af cotangensfunktionen fra dens ækvivalent i sinus og cosinus er bevist.
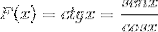
Det behandles som afledt af en funktionsopdeling
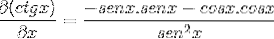
Efter at have udledt er faktorerne grupperet, og målet er at efterligne de pythagoreiske identiteter
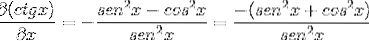
Ved at erstatte identiteterne og anvende gensidighed opnås udtrykket
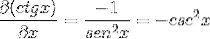
Bevis pr. Definition af afledt
Følgende udtryk svarer pr. Definition til derivatet. Hvor afstanden mellem funktionens 2 punkter nærmer sig nul.
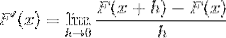
Udskiftning af cotangenten har vi:
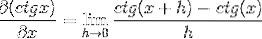
Identiteter anvendes til summen af argumenter og gensidighed
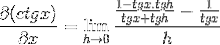
Brækkeren af tælleren betjenes traditionelt
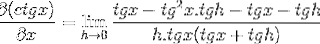
Vi fjerner de modsatte elementer og tager en fælles faktor
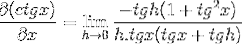
Anvendelse af Pythagoras identiteter og gensidighed skal vi
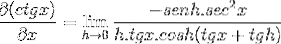
Elementerne, der evalueres i x, er konstante med hensyn til grænsen, derfor kan de forlade argumentet for dette. Derefter anvendes egenskaber ved trigonometriske grænser.
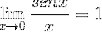
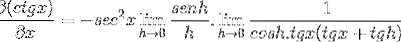
Grænsen evalueres
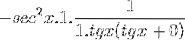
Derefter indregnes det, indtil den ønskede værdi er nået
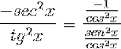
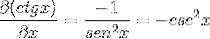
Afledningen af cotangenten demonstreres således som det modsatte af kvadratet af cosecanten.
Løst øvelser
Øvelse 1
Baseret på funktionen f (x) defineres udtrykket f '(x)
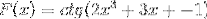
Den tilsvarende afledning anvendes under overholdelse af kædereglen
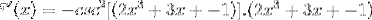
Udleder argumentet
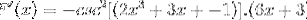
Nogle gange er det nødvendigt at anvende gensidige eller trigonometriske identiteter for at tilpasse løsningerne.
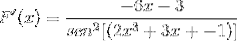
Øvelse 2
Definer det differentielle udtryk, der svarer til F (x)
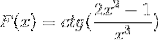
I henhold til afledningsformlen og under overholdelse af kædereglen
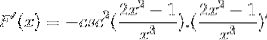
Argumentet er afledt, mens resten forbliver den samme
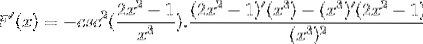
Udleder alle elementerne
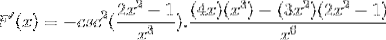
Drift på en traditionel måde produkter af samme base
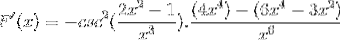
De lige elementer tilføjes, og den fælles faktor ekstraheres
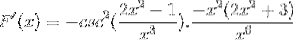
Skilte forenkles og betjenes. Vej til fuldt afledt udtryk
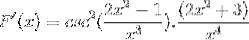
Referencer
- Trigonometrisk serie, bind 1. A. Zygmund. Cambridge University Press, 2002
- Beregning af en enkelt variabel. Ron Larson, Bruce H. Edwards. Cengage Learning, 10. nov 2008
- Calculus med trigonometri og analytisk geometri. John H. Saxon, John Saxon, Frank Wang, Diana Harvey. Saxon Publishers, 1988
- Multivariabel analyse. Satish Shirali, Harkrishan Lal Vasudeva. Springer Science & Business Media, 13. dec. 2010
- Systemdynamik: Modellering, simulering og kontrol af mekatroniske systemer. Dean C. Karnopp, Donald L. Margolis, Ronald C. Rosenberg. John Wiley & Sons, 7. mar 2012
- Calculus: Matematik og modellering. William Bauldry, Joseph R. Fiedler, Frank R. Giordano, Ed Lodi, Rick Vitray. Addison Wesley Longman, 1. jan 1999



Endnu ingen kommentarer